Un ingénieur travaillant dans une entreprise de dispositifs médicaux souhaite déterminer si le nouveau tensiomètre fabriqué par sa société est équivalent à un appareil du même type fabriqué par une autre entreprise. L'ingénieur mesure la tension artérielle systolique d'un échantillon aléatoire de 60 personnes à l'aide des deux appareils.
Pour déterminer si les deux tensiomètres sont équivalents, l'ingénieur utilise une régression orthogonale. Avant la collecte des données pour la régression orthogonale, l'ingénieur a séparé les études sur chaque appareil pour estimer les variances. La variance du nouvel appareil était de 1,08. La variance de l'appareil de l'autre entreprise était de 1,2. L'ingénieur décide de désigner le nouvel appareil comme variable de réponse, et l'appareil de l'autre société comme variable de prévision. Ainsi, le rapport de variance d'erreur est 1,08 / 1,2 = 0,9.
Remarque
Si l'ingénieur décidait d'inverser les attributions de variables, le rapport de variance d'erreur serait 1,2 / 1,08 = 1,1111.
- Ouvrez le fichier de données échantillons, PressionSanguine.MWX.
- Sélectionnez .
- Dans la zone Réponse (Y), saisissez Nouveau.
- Dans la zone Prédicteur (X), saisissez Actuel.
- Dans la zone Rapport des variances des erreurs (Y/X), saisissez 0,90.
- Cliquez sur OK.
Interprétation des résultats
Si l'une des conditions suivantes est avérée, les résultats prouvent que les tensiomètres ne sont
pas équivalents :
- L'intervalle de confiance pour la pente ne contient pas 1.
- L'intervalle de confiance pour la constante ne contient pas 0.
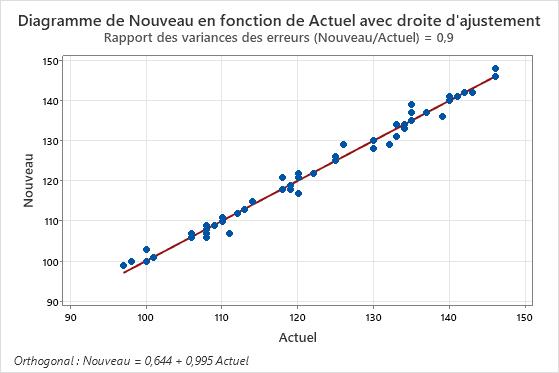
Rapport des variances des erreurs (Nouveau/Actuel) : 0,9
Equation de régression
Nouveau = 0,644 + 0,995 Actuel
Nouveau = 0,644 + 0,995 Actuel
Coefficients
| Prédicteur | Coeff | Coef ErT | Z | P | IC 95 % approx. |
|---|---|---|---|---|---|
| Constante | 0,64441 | 1,74470 | 0,3694 | 0,712 | (-2,77513; 4,06395) |
| Actuel | 0,99542 | 0,01415 | 70,3461 | 0,000 | (0,96769; 1,02315) |
Variances d'erreur
| Variable | Variance |
|---|---|
| Nouveau | 1,07856 |
| Actuel | 1,19840 |