Sur ce thème
Fonction de liaison
Minitab propose trois fonctions de liaison : logit (par défaut), normit et gompit. Les fonctions de liaisons vous permettent d'ajuster un grand nombre de modèles de réponse ordinale. La fonction logit est l'inverse de la fonction de répartition logistique cumulée standard. La fonction normit, aussi appelée probit, est l'inverse de la fonction de répartition normale cumulée standard. La fonction gompit, aussi connue comme log-log complémentaire, est l'inverse de la fonction de répartition de Gompertz.
Formule
g(χk) = θk +x'β, k = 1, ..., K-1
La fonction de liaison est l'inverse d'une loi de distribution. Les fonctions de liaisons et leurs lois correspondantes sont récapitulées ci-après :
| Nom | Fonction de liaison | Loi de distribution |
|---|---|---|
| logit | g(χ) = loge(χ/ (1 – χ)) | logistique |
| normit (probit) |
g(χ) = Φ–1(χ) |
Normal |
| gompit (log-log complémentaire) | g(χ) =loge (–loge(1 – χ)) | Gompertz |
Notation
| Terme | Description |
|---|---|
| K | nombre de catégories distinctes de la réponse |
| χk | probabilité cumulée jusqu'à la catégorie k, (π1+ ...+ πk), incluse |
| g(χk) | vecteur de variables de prédicteurs |
| θk | constante associée à la ke catégorie de réponse distincte |
| x | vecteur de variables de prédicteurs |
| β | vecteur des coefficients associés aux prédicteurs |
Combinaison de facteurs/covariables
Décrit un ensemble unique de valeurs de facteurs/covariables dans un fichier de données. Minitab calcule les probabilités d'événements, les valeurs résiduelles et d'autres mesures de diagnostic pour chaque combinaison de facteurs/covariables.
Par exemple, si un fichier de données inclut des facteurs relatifs au sexe et à l'origine ethnique et la covariable relative à l'âge, la combinaison de ces prédicteurs peut contenir autant de combinaisons de covariables que de sujets. Si un fichier de données inclut uniquement les facteurs relatifs au sexe et à l'origine ethnique, les deux étant codés à deux niveaux, il existe seulement quatre combinaisons de facteurs/covariables possibles. Si vous saisissez les données comme des effectifs (ou des réussites, des essais ou des échecs), chaque ligne contient une combinaison de facteurs/covariables.
Probabilité d'événement
Les probabilités d'événement sont πk pour k = 1, 2, ..., K.
Formule
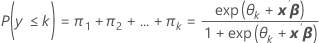
Notation
| Terme | Description |
|---|---|
| k | est égal à 1, ..., K – 1 |
| θk | constante |
| β | vecteur des coefficients dans l'équation logit |
Probabilité cumulée d'événement
Probabilité que la réponse se situe dans la catégorie k ou en dessous, pour chaque k possible. La ke probabilité cumulée est la suivante :
Formule
P(y k) = p1 + ... + pk,k = 1, ... , K
k) = p1 + ... + pk,k = 1, ... , K
Les probabilités cumulées reflètent l'ordre de la réponse. Pour un modèle avec k catégories de réponse :
P(y 1) <P(y
1) <P(y 2)
2)  …
… P(y
P(y K) = 1
K) = 1

Coefficient
Minitab utilise le modèle des probabilités de succès proportionnel dans lequel un vecteur de prédicteurs, x, a un paramètre β qui décrit l'effet de x sur les probabilités de succès du logarithme de la réponse dans la catégorie k ou en dessous. Minitab supposant un effet identique de x pour toutes les catégories K – 1, un seul coefficient est calculé pour chaque prédicteur. Le coefficient du prédicteur indique que, pour tout k fixe, la variation estimée de la fonction logit de la réponse lorsque le prédicteur est à un niveau est comparée au niveau de référence.
Minitab estime une constante pour chaque catégorie K – 1. Utilisez les estimations des paramètres pour calculer les probabilités estimées de chaque catégorie à l'aide du modèle des probabilités cumulées :
Formule
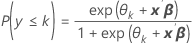
Les coefficients estimés sont calculés à l'aide d'une méthode itérative des moindres carrés repondérés, qui équivaut à l'estimation par le maximum de vraisemblance1,2.
Références
- D.W. Hosmer et S. Lemeshow (2000). Applied Logistic Regression. 2e édition. John Wiley & Sons, Inc.
- P. McCullagh et J.A. Nelder (1992). Generalized Linear Model. Chapman & Hall.
Erreur type des coefficients
Erreur type asymptotique qui indique la précision du coefficient estimé. Plus l'erreur type est petite, plus l'estimation est précise.
Pour plus d'informations, reportez-vous à [1] et à [2].
- A. Agresti (1990). Categorical Data Analysis. John Wiley & Sons, Inc.
- P. McCullagh et J.A. Nelder (1992). Generalized Linear Model. Chapman & Hall.
Z
La valeur de Z sert à déterminer si le prédicteur est associé à la réponse de manière significative. Des valeurs absolues de Z élevées indiquent une relation significative. La valeur de p indique où Z se situe sur la loi normale.
Formule
Z = βi / erreur type
La formule pour la constante est la suivante :
Z = θk / erreur type
Pour les petits échantillons, le test du rapport de vraisemblance peut être un test de signification plus fiable.
valeur de p (P)
Utilisée dans les tests d'hypothèse pour vous aider à décider de rejeter ou non une hypothèse nulle. La valeur de p est la probabilité d'obtenir une statistique de test au moins aussi extrême que la valeur réelle que vous avez calculée, si l'hypothèse nulle est vérifiée. Une valeur limite couramment utilisée pour la valeur de p est 0,05. Par exemple, si la valeur de p d'une statistique de test est inférieure à 0,05, rejetez l'hypothèse nulle.
Rapport des probabilités de succès
Minitab utilise un modèle de probabilités de succès proportionnel pour la régression logistique ordinale. Un seul paramètre et un seul rapport des probabilités de succès sont calculés pour chaque prédicteur. Le rapport des probabilités de succès utilise les probabilités cumulées et leurs compléments. Pour un prédicteur à 2 niveaux x 1 et x 2, le rapport des probabilités de succès cumulées est le suivant :
Formule
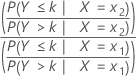
Intervalle de confiance
Formule
L'intervalle de confiance du grand échantillon pour βi est le suivant :
β i + Zα /2* (erreur type)
Pour obtenir l'intervalle de confiance des rapports des probabilités de succès, utilisez un exposant pour les limites supérieure et inférieure de l'intervalle de confiance. L'intervalle indique l'étendue des probabilités de succès pour chaque variation d'unité du prédicteur.
Notation
| Terme | Description |
|---|---|
| α | seuil de signification |
Log de vraisemblance
Dérivée des fonctions de densité de probabilité individuelle, l'expression est maximisée pour générer des valeurs optimales de β. Le log de vraisemblance ne peut pas être utilisé seul comme mesure de l'ajustement, car il dépend de l'effectif de l'échantillon. Par contre, vous pouvez y recourir pour comparer deux modèles.
Pour la régression logistique ordinale, il existe n vecteurs multinomiaux indépendants, chacun ayant k catégories. Ces observations sont traduites par y1, ..., yn, où yi = (yi1, ..., yik) et Σj yij = mi est fixe pour chaque i. A partir de la ie observation yi, la contribution au log de vraisemblance est la suivante :
Formule
L(πi ; yi) = Σk yik log πik
Le log de vraisemblance total est une somme des contributions de chacune des n observations :
L(π ; y) = Σi L(πi ; yi)
Notation
| Terme | Description |
|---|---|
| πik | probabilité de la ie observation pour la ke catégorie |
Matrice de variance/covariance
Matrice carrée avec les dimensions p + K – 1. La variance de chaque coefficient figure dans la cellule en diagonale et la covariance de chaque paire de coefficients figure dans la cellule hors diagonale appropriée. La variance est l'erreur type du carré du coefficient.
La matrice de variance/covariance est asymptotique ; elle est obtenue à partir de la dernière itération de la valeur inverse de la matrice d'informations.
Notation
| Terme | Description |
|---|---|
| p | nombre de prédicteurs |
| K | nombre de catégories dans la réponse |
Pearson
Statistique récapitulative fondée sur les valeurs résiduelles de Pearson, qui indique le degré d'ajustement du modèle à vos données. La méthode de Pearson n'est pas utile lorsque le nombre de valeurs distinctes de la covariable est approximativement égal au nombre d'observations, mais elle est utile lorsque vous avez des observations répétées au même niveau de covariable. Les statistiques de test χ2 élevées et les valeurs de p faibles indiquent que le modèle peut ne pas s'ajuster correctement aux données.
La formule est la suivante :
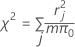
où r = valeur résiduelle de Pearson, m = nombre d'essais dans la je combinaison de facteurs/covariables et π0 = valeur supposée pour la proportion.
somme des carrés d'écart
Statistique récapitulative fondée sur les valeurs résiduelles de la somme des carrés d'écart, qui indique le degré d'ajustement du modèle à vos données. La somme des carrés d'écart n'est pas utile lorsque le nombre de valeurs distinctes de la covariable est approximativement égal au nombre d'observations, mais elle est utile lorsque vous avez des observations répétées au même niveau de covariable. Les valeurs élevées de D et les valeurs de p faibles indiquent que le modèle peut ne pas s'ajuster correctement aux données. Les degrés de liberté pour le test est (k - 1)*J − (p), où k représente le nombre de catégories de la réponse, J représente le nombre de combinaisons de facteurs/covariables et p représente le nombre de coefficients.
La formule est la suivante :
D =2 Σ yik log p ik− 2 Σ yik log π ik
où πik = probabilité de la ie observation pour la ke catégorie.
Mesures d'association
Les paires concordantes et discordantes reflètent la capacité de prévision de votre modèle. Plus les paires sont concordantes, meilleure est la capacité de prévision de votre modèle.
Le tableau de paires concordantes, discordantes et ex aequo est calculé en formant toutes les paires d'observations possibles avec différentes valeurs de réponses. Supposons que les valeurs de réponse sont 1, 2 et 3. Minitab apparie chaque observation ayant la valeur de réponse 1 avec chaque observation ayant les valeurs de réponse 2 et 3, puis apparie chaque observation ayant la valeur de réponse 2 avec chaque observation ayant les valeurs de réponse 1 et 3. Le nombre total de paires est égal au nombre d'observations ayant la réponse 1 multiplié par le nombre d'observations ayant la réponse 2, plus le nombre d'observations ayant la réponse 1 multiplié par le nombre d'observations ayant la réponse 3, plus le nombre d'observations ayant la réponse 2 multiplié par le nombre d'observations ayant la réponse 3.
Pour déterminer si les paires sont concordantes ou discordantes, Minitab calcule les probabilités cumulées prévues de chaque observation et compare ces valeurs pour chaque paire d'observations.
- Paire concordante
- Pour les paires comprenant la plus petite valeur de réponse (1 dans l'exemple ci-dessus), une paire est concordante si la probabilité cumulée jusqu'à la plus petite valeur de réponse est plus élevée pour l'observation avec la plus petite valeur de réponse que pour l'observation avec la valeur de réponse supérieure. Pour les paires avec les valeurs de réponse les plus élevées (2 et 3 dans l'exemple ci-dessus), une paire est concordante si la probabilité cumulée jusqu'à 2 est plus élevée pour l'observation avec la valeur de réponse 2 que pour l'observation avec la valeur de réponse 3.
- Paire discordante
- Pour les paires comprenant la plus petite valeur de réponse (1 dans l'exemple ci-dessus), une paire est discordante si la probabilité cumulée jusqu'à la plus petite valeur de réponse est plus élevée pour l'observation avec la plus grande valeur de réponse que pour l'observation avec la valeur de réponse inférieure. Pour les paires avec les valeurs de réponse les plus élevées (2 et 3 dans l'exemple ci-dessus), une paire est discordante si la probabilité cumulée jusqu'à 2 est plus élevée pour l'observation avec la valeur de réponse 3 que pour l'observation avec la valeur de réponse 2.
- Paires ex aequo
- Une paire est ex aequo si les observations ont des probabilités cumulées égales.
Formule
A partir du tableau des paires concordante, discordante et ex aequo, Minitab calcule les mesures récapitulatives suivantes :



Notation
| Terme | Description |
|---|---|
| nc | nombre de paires concordantes |
| nd | nombre de paires discordantes |
| nt | nombre de paires ex aequo |
| N | nombre total d'observations |
