Sélectionnez la méthode ou la formule de votre choix.
Sur ce thème
Contraintes de paramètres
Appliquez les contraintes de paramètres en transformant les paramètres1.
| Si | Alors |
|---|---|
| a < θ | θ = a + exp( φ ) |
| θ < b | θ = b - exp( φ ) |
| a < θ < b | θ = a +((b - a) / (1 + exp( -φ ))) |
| Terme | Description |
|---|---|
| a et b | constantes numériques |
| θ | paramètres |
| φ | paramètres transformés |
Minitab réalise ces transformations et affiche les résultats dans les termes des paramètres d'origine.
- Bates et Watts (1988). Nonlinear Regression Analysis and Its Applications. John Wiley & Sons, Inc.
Erreur type de l'estimation du paramètre
L'erreur standard approximative de l'estimation de θp est S, multiplié par la racine carrée de l'élément diagonal p de 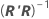 , qui s'écrit comme suit :
, qui s'écrit comme suit :

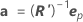

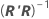 , qui s'écrit comme suit :
, qui s'écrit comme suit :

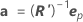

Notation
| Terme | Description |
|---|---|
| n | ne observation |
| N | nombre total d'observations |
| p | nombre de paramètres libres (non verrouillés) |
| R | matrice R (triangulaire supérieure) dans la décomposition QR de Vi pour l'itération finale |
| V0 | matrice de gradient = (∂f(xn, θ) / ∂θp), P par 1 vecteur des dérivées partielles de f(x0, θ), évaluée à θ* |
| S |
 |
Matrice de corrélation pour les estimations des paramètres
La matrice de variance/covariance approximative pour les estimations des paramètres est la suivante :
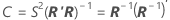
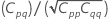

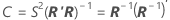
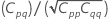

Notation
| Terme | Description |
|---|---|
| R | matrice R (triangulaire supérieure) dans la décomposition QR de Vi pour l'itération finale |
| P | nombre de paramètres libres (non verrouillés) |
| v0 | matrice de gradient = (∂f(xn, θ) / ∂θp), P par 1 vecteur des dérivées partielles de f(x0, θ), évaluée à θ* |
| θ | paramètres |
Intervalles de confiance de vraisemblance du profil pour les paramètres
Soit θ = (θ1, . . . . θp) * avec θ* comme itération finale pour θ.
Les limites de confiance (100 1 - α) % fondées sur la vraisemblance satisfont les conditions suivantes :
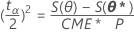
où S(θp) est la SCE obtenue en maintenant θp fixe et en minimisant les autres paramètres1. Cela équivaut à résoudre l'équation suivante :
S(θp) = S(θ*) + (tα/2)2 CME
Notation
| Terme | Description |
|---|---|
| θ | paramètres |
| n | ne observation |
| N | nombre total d'observations |
| P | nombre de paramètres libres (non verrouillés) |
| tα/2 | point supérieur α/2 de la loi de distribution t avec N – P degrés de liberté |
| S(θ) | Somme du carré de l'erreur |
| CA MOY ERR | carré moyen de l'erreur |
- Bates et Watts (1988). Nonlinear Regression Analysis and Its Applications. John Wiley & Sons, Inc.
