Méthodes dans Régression non linéaire

La fonction de prévision pour l'observation n est notée de la façon suivante :

Minitab considère la fonction de prévision pour toutes les observations N comme une fonction à valeurs vectorielles des paramètres, comme suit :

qui est un vecteur N X 1 avec les éléments .

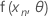
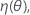
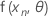La matrice jacobienne de η est une matrice N X P avec des éléments égaux aux dérivées partielles de la fonction de prévision concernant les paramètres :

Soit Vⁱ = V(θⁱ), la matrice jacobienne évaluée à θⁱ, l'estimation de paramètre après l'itération i.

Une approximation linéaire de η est donc la suivante :

qui constitue la base pour la méthode de Gauss-Newton et pour les interférences approximatives.

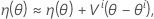
Soit θ* l'estimation des moindres carrés.

Par défaut, Minitab utilise la méthode de Gauss-Newton pour déterminer l'estimation des moindres carrés. La méthode utilise une approximation linéaire pour la fonction de prévision pour améliorer de manière itérative une supposition d'origine θ⁰ pour θ. Cela signifie que Minitab étend la fonction de prévision f(x_n,θ) dans une série de Taylor de premier ordre concernant θ⁰, comme suit :

où

avec p = 1, 2,..., p

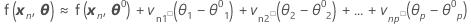
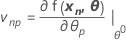
Y compris tous les cas N

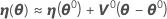
où V⁰ est la matrice dérivée NxP avec les éléments {v_np}. Cela équivaut à déterminer approximativement les valeurs résiduelles, z(θ) = y - η(θ), de la façon suivante :

où

et

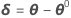
Minitab calcule l'incrément de Gauss δ⁰ pour minimiser la somme des carrés des valeurs résiduelles approximatives 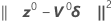, à l'aide de :

et donc : .

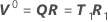
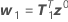
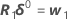Le point

doit désormais être plus proche de y que η(θ⁰), et Minitab utilise la valeur θ¹ = θ⁰ + δ⁰ pour réaliser une autre itération en calculant de nouvelles valeurs résiduelles z¹ = y - η(θ¹), une nouvelle matrice dérivée V¹ et un nouvel incrément. Minitab répète ce procédé jusqu'à atteindre une convergence, c'est-à-dire lorsque l'incrément est tellement petit qu'il n'existe aucune variation utile des éléments du vecteur de paramètre.

L'incrément de Gauss-Newton engendre parfois une augmentation de la somme des carrés. Lorsque cela se produit, l'approximation linéaire est toujours proche de la surface réelle pour une zone suffisamment petite autour de η(θ⁰). Pour réduire la somme des carrés, Minitab introduit un facteur d'étape λ et procède au calcul suivant :

Minitab commence avec λ = 1 et le divise par deux jusqu'à ce que S(θ¹) < S(θ⁰).

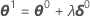
1. Bates et Watts (1988). Nonlinear Regression Analysis and Its Applications. John Wiley & Sons, Inc.

Lorsque les colonnes dans votre matrice de gradient V sont colinéaires, celle-ci peut devenir anormale, ce qui entraîne un comportement irrégulier des itérations de Gauss-Newton. Pour contourner ce problème, Minitab peut remplacer l'incrément de Gauss-Newton par l'algorithme de Levenberg, un bon compromis :

ou l'algorithme de Marquardt :

où k est un facteur de conditions et D une matrice diagonale avec des entrées égales aux éléments diagonaux de V^TV. Le sens de δ(k) est intermédiaire entre le sens de l'incrément de Gauss-Newton (k → 0) et le sens de la plus grande pente :

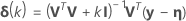
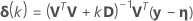
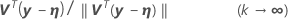.¹

1. Bates et Watts (1988). Nonlinear Regression Analysis and Its Applications. John Wiley & Sons, Inc.

Par défaut, Minitab annonce une convergence lorsque le décalage relatif est inférieur à 1,0e-5. Cela garantit que les interférences ne sont pas matériellement concernées par le fait que le vecteur de paramètre actuel est inférieur à 0,001 % du rayon du disque de zone de confiance découlant du point des moindres carrés¹.

1. Bates et Watts (1988). Nonlinear Regression Analysis and Its Applications. John Wiley & Sons, Inc.