Sur ce thème
Etape 1 : Déterminer si la droite de régression est ajustée à vos données
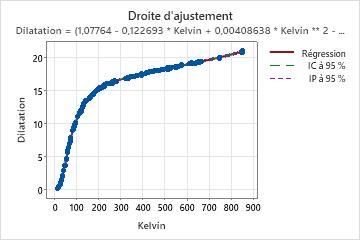
Si votre modèle non linéaire contient un seul prédicteur, Minitab affiche la droite d'ajustement indiquant la relation entre les données de réponse et de prédicteur. Le graphique comprend la droite de régression, qui représente l'équation de régression. Vous pouvez également afficher les intervalles de prévision et de confiance à 95 % sur le graphique.
- L'échantillon contient le nombre approprié d'observations sur l'étendue entière des valeurs de prédicteur.
- Le modèle s'ajuste parfaitement à la courbure des données. Pour déterminer le modèle qui convient le mieux, étudiez la droite d'ajustement, l'erreur type de la régression (S) et le test d'inadéquation de l'ajustement lorsque vos données contiennent des répliques.
- Recherchez les éventuelles valeurs aberrantes susceptibles d'influencer les résultats. Essayez de déterminer la cause de toutes les valeurs aberrantes. Corrigez les erreurs de mesure ou d’entrée des données. Pensez éventuellement à supprimer les valeurs de données associées à des événements anormaux et uniques (causes spéciales). Ensuite, répétez l'analyse. Pour plus d'informations sur la détection des valeurs aberrantes, reportez-vous à la rubrique Observations aberrantes.
Etape 2 : Examiner la relation entre les prédicteurs et la réponse
Utilisez l'équation de régression pour décrire la relation entre la réponse et les termes du modèle. L'équation de régression est une représentation algébrique de la droite de régression. Entrez la valeur de chaque prédicteur dans l'équation pour calculer la valeur de réponse moyenne. Contrairement à la régression linéaire, une équation de régression non linéaire peut prendre de nombreuses formes.
Pour les équations non linéaires, déterminer l'effet de chaque prédicteur sur la réponse peut s'avérer moins intuitif que pour les équations linéaires. Contrairement aux estimations de paramètres dans les modèles linéaires, aucune interprétation cohérente des estimations de paramètres n'est possible dans les modèles non linéaires. La bonne interprétation de chaque paramètre dépend de la fonction de prévision et de la place occupée par le paramètre. Si votre modèle non linéaire contient un seul prédicteur, évaluez la droite d'ajustement pour voir la relation entre le prédicteur et la réponse.
Pour déterminer si l'estimation d'un paramètre est statistiquement significative, utilisez les intervalles de confiance pour les paramètres. Le paramètre est statistiquement significatif si l'intervalle exclut la valeur de l'hypothèse nulle. Minitab ne peut pas calculer les valeurs de p pour les paramètres dans une régression non linéaire. Pour la régression linéaire, la valeur d'hypothèse nulle de chaque paramètre est 0, c'est-à-dire aucun effet, et la valeur de p est fondée sur cette valeur. En revanche, pour la régression non linéaire, la valeur correcte d'hypothèse nulle de chaque paramètre dépend de la fonction de prévision et de la place qu'y occupe le paramètre.
Pour certains fichiers de données, fonctions de prévision et niveaux de confiance, il est possible qu'au moins une des deux bornes de confiance n'existe pas. Minitab signale les résultats manquants à l'aide d'un astérisque. Si une borne d'un intervalle de confiance est manquante, vous pouvez essayer d'utiliser un niveau de confiance plus faible pour obtenir un intervalle bilatéral.
Le fait d'observer une convergence sur une solution ne garantit pas forcément que l'ajustement du modèle est optimal ou que la somme des carrés de l'erreur (SCE) est minimale. Il est possible d'obtenir une convergence sur des valeurs de paramètres incorrectes à cause d'un minimum de SCE local ou d'une fonction de prévision erronée, par exemple. Par conséquent, il est impératif d'examiner les valeurs des paramètres, la droite d'ajustement et les graphiques des valeurs résiduelles pour déterminer si le modèle convient et si les valeurs des paramètres sont raisonnables.
Equation
** 3) / (1 - 0,00576099 * Kelvin + 0,000240537 * Kelvin ** 2 - 1,23144E-07 * Kelvin ** 3)
Résultat principal : équation
Dans ces résultats, on observe un prédicteur et sept estimations de paramètres. La variable de réponse est Dilatation et la variable de prédiction correspond à la température sur l'échelle thermodynamique (de Kelvin). L'équation longue décrit la relation entre la réponse et les prédicteurs. L'effet d'une augmentation de 1 kelvin sur la dilatation du cuivre dépend fortement de la température initiale. L'effet des variations de températures sur la dilatation du cuivre est difficile à résumer. Etudiez la droite d'ajustement pour déterminer la relation entre le prédicteur et la réponse.
Si vous entrez une valeur de température sur l'échelle de Kelvin dans l'équation, le résultat est la valeur ajustée de la dilatation du cuivre.
Etape 3 : Déterminer l'ajustement du modèle aux données
Pour déterminer le degré d'ajustement du modèle à vos données, examinez les statistiques fournies dans le tableau récapitulatif du modèle et le tableau d'inadéquation de l'ajustement.
- S
-
Utilisez S pour évaluer la capacité du modèle à décrire la réponse.
S est mesuré en unités de la variable de réponse et représente la distance entre les valeurs de données et les valeurs ajustées. Plus S est petit, mieux le modèle décrit la réponse. Cependant, une faible valeur de S n'indique pas en soi que le modèle respecte les hypothèses du modèle. Vous devez examiner les graphiques des valeurs résiduelles pour vérifier les hypothèses.
- Inadéquation de l'ajustement
-
Minitab affiche automatiquement le tableau d'inadéquation de l'ajustement lorsque vos données contiennent des répliques. Ces dernières correspondent à plusieurs observations ayant des valeurs de prédicteurs identiques. Si vos données ne contiennent pas de répliques, il est impossible de calculer l'erreur pure nécessaire pour effectuer ce test. Des valeurs de réponse différentes pour les répliques constituent une erreur pure car seule la variation aléatoire peut entraîner des différences entre des valeurs de réponse observées.
Pour déterminer si le modèle rend correctement compte de la relation entre la réponse et les prédicteurs, comparez la valeur de p du test d'inadéquation de l'ajustement à votre seuil de signification pour évaluer l'hypothèse nulle. L'hypothèse nulle pour le test d'inadéquation de l'ajustement est que le modèle rend correctement compte de la relation entre la réponse et les prédicteurs. En général, un seuil de signification (noté alpha ou α) de 0,05 fonctionne bien. Un seuil de signification de 0,05 indique 5 % de risque de conclure à tort que le modèle ne rend pas correctement compte de la relation entre la réponse et les prédicteurs.- Valeur de p ≤ α : l'inadéquation de l'ajustement est statistiquement significative.
- Si la valeur de p est inférieure ou égale au seuil de signification, vous pouvez en conclure que le modèle ne rend pas correctement compte de la relation. Pour améliorer le modèle, vous devez peut-être ajouter des termes ou transformer vos données.
- Valeur de p > α : l'inadéquation de l'ajustement n'est pas statistiquement significative.
-
Si la valeur de p est supérieure au seuil de signification, le test ne détecte aucune inadéquation de l'ajustement.
Inadéquation de l'ajustement
| Source | DL | Somme des carrés | CM | F | P |
|---|---|---|---|---|---|
| Erreur | 229 | 1,53244 | 0,0066919 | ||
| Inadéquation de l'ajustement | 228 | 1,52583 | 0,0066922 | 1,01 | 0,679 |
| Erreur pure | 1 | 0,00661 | 0,0066125 |
Récapitulatif
| Itérations | 15 |
|---|---|
| SCE finale | 1,53244 |
| DLE | 229 |
| MSE | 0,0066919 |
| S | 0,0818039 |
Résultats principaux : S, inadéquation de l'ajustement
Dans ces résultats, S indique que l'écart type de la distance entre les valeurs de données et les valeurs ajustées est d'environ 0,08 unité. La valeur de p pour le test d'inadéquation de l'ajustement est de 0,679, ce qui ne fournit aucune preuve que le modèle s'ajuste mal aux données.
Etape 4 : Déterminer si votre modèle vérifie les hypothèses de l'analyse
Les graphiques des valeurs résiduelles permettent de déterminer si le modèle est adapté et si les hypothèses de l'analyse sont vérifiées. Si elles ne le sont pas, il se peut que le modèle ne soit pas ajusté aux données et vous devez être prudent lors de l'interprétation des résultats.
Pour plus d'informations sur la manière de traiter les schémas dans les graphiques des valeurs résiduelles, reportez-vous à la rubrique Graphiques des valeurs résiduelles pour Régression non linéaire et cliquez sur le nom du graphique des valeurs résiduelles dans la liste située en haut de la page.
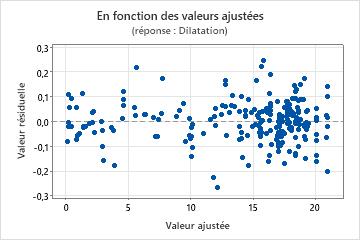
Graphique des valeurs résiduelles en fonction des valeurs ajustées
Utilisez le diagramme des valeurs résiduelles en fonction des valeurs ajustées pour vérifier l'hypothèse selon laquelle les valeurs résiduelles suivent une loi normale et ont une variance constante. Dans l'idéal, les points doivent être répartis aléatoirement des deux côtés de 0, sans schéma reconnaissable.
| Schéma | Ce que le schéma indique |
|---|---|
| Eparpillement ou répartition déséquilibrée des valeurs résiduelles en fonction des valeurs ajustées | Variance non constante |
| Curviligne | Un terme d'ordre supérieur manquant |
| Un point très éloigné de zéro | Une valeur aberrante |
| Un point éloigné des autres points dans le sens des x | Un point influent |
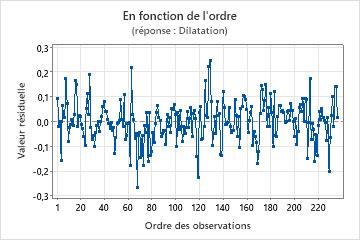
Graphique des valeurs résiduelles en fonction de l'ordre
Tendance
Equipe
Cycle
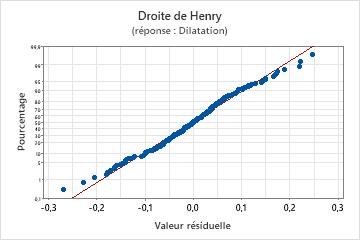
Droite de Henry des valeurs résiduelles
Utilisez la droite de Henry des valeurs résiduelles afin de vérifier l'hypothèse selon laquelle les valeurs résiduelles sont normalement distribuées. La droite de Henry des valeurs résiduelles doit suivre approximativement une ligne droite.
| Schéma | Ce que le schéma indique |
|---|---|
| Une ligne qui n'est pas droite | Non-normalité |
| Un point éloigné de la ligne | Une valeur aberrante |
| Une modification de la pente | Une variable non identifiée |