Sur ce thème
Droite d'ajustement
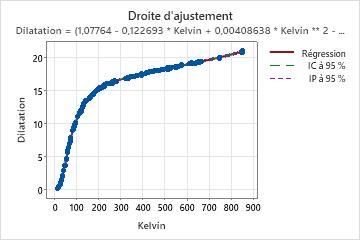
Si votre modèle non linéaire contient un seul prédicteur, Minitab affiche la droite d'ajustement indiquant la relation entre les données de réponse et de prédicteur. Le graphique comprend la droite de régression, qui représente l'équation de régression. Vous pouvez également afficher les intervalles de prévision et de confiance à 95 % sur le graphique.
Interprétation
- L'échantillon contient le nombre approprié d'observations sur l'étendue entière des valeurs de prédicteur.
- Le modèle s'ajuste parfaitement à la courbure des données. Pour déterminer le modèle qui convient le mieux, étudiez la droite d'ajustement, l'erreur type de la régression (S) et le test d'inadéquation de l'ajustement lorsque vos données contiennent des répliques.
- Recherchez les éventuelles valeurs aberrantes susceptibles d'influencer les résultats. Essayez de déterminer la cause de toutes les valeurs aberrantes. Corrigez les erreurs de mesure ou d’entrée des données. Pensez éventuellement à supprimer les valeurs de données associées à des événements anormaux et uniques (causes spéciales). Ensuite, répétez l'analyse. Pour plus d'informations sur la détection des valeurs aberrantes, reportez-vous à la rubrique Observations aberrantes.
Equation
Utilisez l'équation de régression pour décrire la relation entre la réponse et les termes du modèle. L'équation de régression est une représentation algébrique de la droite de régression. Entrez la valeur de chaque prédicteur dans l'équation pour calculer la valeur de réponse moyenne. Contrairement à la régression linéaire, une équation de régression non linéaire peut prendre de nombreuses formes.
Pour les équations non linéaires, déterminer l'effet de chaque prédicteur sur la réponse peut s'avérer moins intuitif que pour les équations linéaires. Contrairement aux modèles linéaires, les modèles non linéaires ne permettent aucune interprétation constante des estimations de paramètres. La bonne interprétation de chaque paramètre dépend de la fonction de prévision et de la place qu'y occupe le paramètre. Si votre modèle non linéaire ne contient qu'un seul prédicteur, étudiez la droite d'ajustement pour déterminer la relation entre le prédicteur et la réponse.
Le fait d'observer une convergence sur une solution ne garantit pas forcément que l'ajustement du modèle est optimal ou que la somme des carrés de l'erreur (SCE) est minimale. Il est possible d'obtenir une convergence sur des valeurs de paramètres incorrectes à cause d'un minimum de SCE local ou d'une fonction de prévision erronée, par exemple. Par conséquent, il est impératif d'examiner les valeurs des paramètres, la droite d'ajustement et les graphiques des valeurs résiduelles pour déterminer si le modèle convient et si les valeurs des paramètres sont raisonnables.
Interprétation
Dans ces résultats, on observe un prédicteur et sept estimations de paramètres. La variable de réponse est Dilatation et la variable de prédiction correspond à la température sur l'échelle thermodynamique (de Kelvin). L'équation longue décrit la relation entre la réponse et les prédicteurs. L'effet d'une augmentation de 1 kelvin sur la dilatation du cuivre dépend fortement de la température initiale. L'effet des variations de températures sur la dilatation du cuivre est difficile à résumer. Etudiez la droite d'ajustement pour déterminer la relation entre le prédicteur et la réponse.
Si vous entrez une valeur de température sur l'échelle de Kelvin dans l'équation, le résultat est la valeur ajustée de la dilatation du cuivre.
Equation
** 3) / (1 - 0,00576099 * Kelvin + 0,000240537 * Kelvin ** 2 - 1,23144E-07 * Kelvin ** 3)
IC à 95 %
L'intervalle de confiance pour la valeur ajustée fournit une étendue de valeurs possibles pour la réponse moyenne en fonction des paramètres spécifiés pour les prédicteurs.
Interprétation
Utilisez l'intervalle de confiance afin d'évaluer l'estimation de la valeur ajustée pour les valeurs observées des variables.
Par exemple, avec un niveau de confiance de 95 %, vous pouvez être sûr à 95 % que l'intervalle de confiance comprend la moyenne de la population pour les valeurs indiquées des variables du modèle. L'intervalle de confiance vous aide à évaluer la signification pratique de vos résultats. Utilisez vos connaissances spécialisées pour déterminer si l'intervalle de confiance comporte des valeurs ayant une signification pratique pour votre situation. Un grand intervalle de confiance traduit moins de certitude quant à la moyenne des futures valeurs. Si l'intervalle est trop grand pour être utile, envisagez d'augmenter l'effectif de l'échantillon.
IP de 95 %
L'intervalle de prévision est une étendue susceptible de contenir une seule réponse future pour une valeur de variable de prévision au vu des paramètres indiqués pour les prédicteurs.
Interprétation
Par exemple, un ingénieur spécialisé dans les matériaux travaillant pour une entreprise de fabrication de meubles élabore un modèle de régression simple pour prévoir la rigidité d'un panneau de particules à partir de la densité du panneau. Il vérifie que le modèle satisfait aux hypothèses de l'analyse. L'analyste utilise ensuite le modèle pour prévoir la rigidité.
L'équation de régression prévoit que la rigidité pour une nouvelle observation sera de 66,995 et que l'intervalle de prévision est de [50, 85]. Bien qu'il est improbable qu'une telle observation ait une rigidité exacte de 66,995, l'intervalle de prévision indique que l'ingénieur peut être certain à 95 % que la valeur réelle sera comprise entre 50 et 85.
L'intervalle de prévision est toujours plus large que l'intervalle de confiance correspondant, car la prévision d'une seule réponse est moins certaine que celle de la moyenne de plusieurs réponses.
