Sur ce thème
Modèles de régression polynomiale
Formule
Vous pouvez ajuster les modèles de régression linéaires, quadratiques ou cubiques suivants :
| Type de modèle | Ordre | Modèle statistique |
|---|---|---|
| linéaire | premier | Y = β0+ β1x + e |
| quadratique | deuxième | Y = β0+ β1x + β2x2+ e |
| cubique | troisième | Y = β0+ β1x + β2x2+ β3x3+ e |
Si vous souhaitez modéliser une courbure, vous pouvez également générer d'autres modèles en utilisant le logarithme décimal (log10) de x et/ou de y pour les modèles linéaires, quadratiques et cubiques. En outre, vous pouvez utiliser le log10 de y pour réduire une asymétrie à droite ou une variance non constante des valeurs résiduelles.
Lorsque Minitab ajuste les modèles quadratiques ou cubiques, il normalise les prédicteurs avant d'estimer les coefficients. La normalisation réduit la multicolinéarité entre les prédicteurs. Ainsi réduite, la multicolinéarité est suffisamment basse pour éviter que Minitab n'exclue des prédicteurs du modèle. Les résultats présentent les coefficients sous forme non normalisée, dans les unités d'origine des prédicteurs.
Coefficient (Coeff)
La formule pour le coefficient ou la pente dans une régression linéaire simple est la suivante :
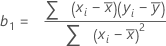
La formule de l'ordonnée à l'origine (b0) est la suivante :

Dans les termes de la matrice, la formule qui calcule le vecteur des coefficients dans la régression multiple est la suivante :
b = (X'X)-1X'y
Notation
| Terme | Description |
|---|---|
| yi | ie valeur de réponse observée |
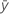 | réponse moyenne |
| xi | ie valeur de prédicteur |
 | prédicteur de la moyenne |
| X | matrice du plan |
| y | matrice de la réponse |
S

Notation
| Terme | Description |
|---|---|
| CA MOY ERR | carré moyen de l'erreur |
R carré


R2 peut également être calculé comme la corrélation au carré entre y et 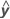 .
.
Notation
| Terme | Description |
|---|---|
| SC | Somme des carrés |
| y | variable de réponse |
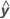 | variable de réponse ajustée |
R carré (ajust)

Notation
| Terme | Description |
|---|---|
| CM | Carré moyen |
| SC | Somme des carrés |
| DL | Degrés de liberté |
Degrés de liberté (DL)
Les degrés de liberté pour chaque composant du modèle sont les suivants :
| Sources de variation | DL |
|---|---|
| Régression | p |
| Erreur | n – p – 1 |
| Total | n – 1 |
- Les données contiennent plusieurs observations avec les mêmes valeurs de prédicteurs.
- Les données contiennent les points corrects pour estimer les termes supplémentaires absents du modèle.
Notation
| Terme | Description |
|---|---|
| n | nombre d'observations |
| p | nombre de coefficients du modèle, indépendamment de la constante |
SomCar ajust
Somme du carré des distances. La somme des carrés provenant de la régression (Régression SC) est la part de la variation expliquée par le modèle. La somme des carrés des erreurs (Erreur SC) est la part de la variation qui n'est pas expliquée par les données. La somme des carrés totale est la variation totale des données.
Formule

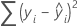
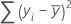
Notation
| Terme | Description |
|---|---|
| yi | ie valeur de réponse observée |
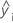 | ie réponse ajustée |
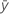 | réponse moyenne |
CM ajust - Erreur
Le carré moyen de l'erreur (également abrégé en CM Erreur ou CME et noté s2) est la variance autour de la droite de régression. La formule est la suivante :

Notation
| Terme | Description |
|---|---|
| yi | ie valeur de réponse observée |
 | ième réponse ajustée |
| n | nombre d'observations |
| p | nombre de coefficients dans le modèle, constante non incluse |
CM ajust - Régression
La formule du carré moyen (CM) de la régression est la suivante :
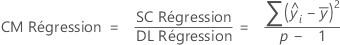
Notation
| Terme | Description |
|---|---|
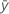 | réponse moyenne |
 | ie réponse ajustée |
| p | nombre de termes dans le modèle |
CM ajust - Total
La formule pour le carré moyen (CM) total est la suivante :

Notation
| Terme | Description |
|---|---|
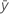 | réponse moyenne |
| yi | ie valeur de réponse observée |
| n | nombre d'observations |
Valeur F
Les formules pour les statistiques F sont les suivantes :
- F(Régression)
-

- F(Terme)
-

- F(Inadéquation de l'ajustement)
-

Notation
| Terme | Description |
|---|---|
| CM Régression | Mesure de la variation de la réponse expliquée par le modèle actuel. |
| CM Erreur | Mesure de la variation que le modèle n'explique pas. |
| CM Terme | Mesure de l'ampleur de la variation expliquée par un terme après la prise en compte des autres termes du modèle. |
| CM Inadéquation de l'ajustement | Mesure de la variation de la réponse qui peut être modélisée en ajoutant d'autres termes au modèle. |
| CM Erreur pure | Mesure de la variation dans les données de réponse répétées. |
Valeur de p - Tableau d'analyse de la variance
La valeur de p est une probabilité calculée à partir d'une loi F avec les degrés de liberté (DL) suivants :
- DL en numérateur
- somme des degrés de liberté pour le ou les termes du test
- DL en dénominateur
- degrés de liberté pour l'erreur
Formule
1 − P(F ≤ fj)
Notation
| Terme | Description |
|---|---|
| P(F ≤ f) | fonction de répartition de la loi F |
| f | statistique f pour le test |
Valeur résiduelle (Val rés)
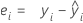
Notation
| Terme | Description |
|---|---|
| ei | ie valeur résiduelle |
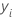 | ie valeur de réponse observée |
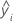 | ie réponse ajustée |
