Sur ce thème
- Etape 1 : Déterminer si l'association entre la réponse et le terme est statistiquement significative
- Etape 2 : Déterminer si la droite de régression est ajustée à vos données
- Etape 3 : Etudier la relation entre le terme et la réponse
- Etape 4 : Déterminer l'ajustement du modèle à vos données
- Etape 5 : Déterminer si votre modèle vérifie les hypothèses de l'analyse
Etape 1 : Déterminer si l'association entre la réponse et le terme est statistiquement significative
- Valeur de p ≤ α : l'association est statistiquement significative
- Si la valeur de p est inférieure ou égale au seuil de signification, vous pouvez conclure qu'il existe une association statistiquement significative entre la variable de réponse et le terme. Si vous ajustez un modèle quadratique ou cubique et que les termes quadratiques ou cubiques sont significatifs, vous pouvez en conclure que les données contiennent une courbure.
- Valeur de p > α : l'association n'est pas statistiquement significative
-
Si la valeur de p est supérieure au seuil de signification, vous ne pouvez pas conclure qu'il existe une association statistiquement significative entre la variable de réponse et le terme. Si vous ajustez un modèle quadratique ou cubique et que les termes quadratiques ou cubiques ne sont pas statistiquement significatifs, il est sans doute nécessaire de sélectionner un modèle différent.
Analyse de la variance
| Source | DL | Somme des carrés | CM | F | P |
|---|---|---|---|---|---|
| Régression | 2 | 12189,4 | 6094,70 | 106,54 | 0,000 |
| Erreur | 26 | 1487,3 | 57,21 | ||
| Total | 28 | 13676,7 |
Analyse séquentielle de la variance
| Source | DL | Somme des carrés | F | P |
|---|---|---|---|---|
| Linéaire | 1 | 11552,8 | 146,86 | 0,000 |
| Quadratique | 1 | 636,6 | 11,13 | 0,003 |
Principal résultat : Valeur de P
Dans ces résultats, la valeur de p est de 0,000 pour le terme linéaire Densité et de 0,003 pour le terme quadratique Densité2. Les deux valeurs sont inférieures au seuil de signification de 0,05. Ces résultats indiquent que l'association entre la rigidité et la densité est statistiquement significative.
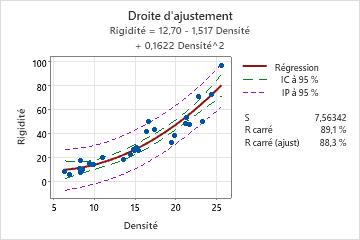
Etape 2 : Déterminer si la droite de régression est ajustée à vos données
- L'échantillon contient le nombre approprié d'observations sur l'étendue entière des valeurs de prédicteur.
- Le modèle s'ajuste parfaitement à n'importe quelle courbure des données. Si vous ajustez un modèle linéaire et constatez une courbure dans les données, répétez l'analyse et sélectionnez le modèle cubique ou quadratique. Pour déterminer le modèle qui convient le mieux, étudiez la droite d'ajustement et les statistiques d'adéquation de l'ajustement. Observez la valeur de p des termes du modèle pour vous assurer qu'ils sont significatifs d'un point de vue statistique, puis appliquez vos connaissances du procédé pour déterminer s'ils le sont également dans la pratique.
- Recherchez les éventuelles valeurs aberrantes susceptibles d'influencer les résultats. Essayez de déterminer la cause de toutes les valeurs aberrantes. Corrigez les erreurs de mesure ou d’entrée des données. Pensez éventuellement à supprimer les valeurs de données associées à des événements anormaux et uniques (causes spéciales). Ensuite, répétez l'analyse. Pour plus d'informations sur la détection des valeurs aberrantes, reportez-vous à la rubrique Observations aberrantes.
Etape 3 : Etudier la relation entre le terme et la réponse
Si la valeur de p du terme est significative, vous pouvez examiner l'équation de régression pour connaître la relation entre le terme et la réponse.
Utilisez l'équation de régression pour décrire la relation entre la réponse et les termes du modèle. L'équation de régression est une représentation algébrique de la droite de régression. L'équation de régression pour le modèle linéaire prend la forme suivante : Y = b0 + b1x1. Dans l'équation de régression, Y représente la variable de réponse, b0 est la constante ou l'ordonnée à l'origine, b1 est le coefficient estimé du terme linéaire (également appelé pente de la droite) et x1 est la valeur du terme.
Le coefficient du terme représente la variation de la réponse moyenne lorsque le terme est modifié d'une unité. Le signe du coefficient indique le sens de la relation entre le terme et la réponse. Si le coefficient est négatif, plus le terme augmente, plus la valeur moyenne de la réponse diminue. Si le coefficient est positif, plus le terme augmente, plus la valeur moyenne de la réponse augmente.
Par exemple, le responsable d'une entreprise considère que les résultats d'un employé à un test de compétences professionnelles peuvent être prévus à l'aide du modèle de régression y = 130 + 4,3x. Dans cette équation, x représente les heures de formation sur les lieux de travail (de 0 à 20) et y représente le résultat au test. Le coefficient, ou la pente, est de 4,3, ce qui signifie que pour chaque nouvelle heure de formation, le résultat moyen au test augmente de 4,3 points.
Pour plus d'informations sur les coefficients, reportez-vous à la rubrique Coefficients de régression.
Rigidité = 12,70 - 1,517 Densité + 0,1622 Densité^2
Récapitulatif du modèle
| S | R carré | R carré (ajust) |
|---|---|---|
| 7,56342 | 89,13% | 88,29% |
Principaux résultats : équation de régression, coefficient
Le coefficient est de –1,517 pour le prédicteur Densité et de 0,1622 pour Densité2. Ainsi, avec une relation quadratique, la rigidité moyenne du panneau de particules augmente plus rapidement avec des grandes valeurs de densité qu'avec des petites valeurs de densité.
Etape 4 : Déterminer l'ajustement du modèle à vos données
Pour déterminer l'ajustement du modèle aux données, étudiez les statistiques d'adéquation de l'ajustement dans le tableau Récapitulatif du modèle.
- R carré
-
Le R2 est le pourcentage de variation dans la réponse qui est expliquée par le modèle.Plus la valeur de R2 est élevée, plus l'ajustement offert par le modèle est bon. Le R2 se situe toujours entre 0 % et 100 %.
La valeur R2 augmente toujours lorsque vous ajoutez des prédicteurs à un modèle. Par exemple, le meilleur modèle à cinq prédicteurs aura toujours une valeur R2 au moins aussi élevée que celle du meilleur modèle à quatre prédicteurs. Par conséquent, R2 est surtout utile pour comparer des modèles de même taille.
- R carré (ajust)
-
Utilisez la valeur R2 ajusté pour comparer des modèles n'ayant pas le même nombre de prédicteurs. R2 augmente toujours lorsque vous ajoutez un prédicteur au modèle, même lorsque ce prédicteur n'apporte aucune amélioration réelle au modèle. La valeur de R2 ajusté intègre le nombre de prédicteurs dans le modèle pour vous aider à choisir le modèle correct.
-
Les petits échantillons ne fournissent pas d'estimation précise de la force de la relation entre la réponse et les prédicteurs. Par exemple, pour obtenir une valeur R2 plus précise, vous devez utiliser un échantillon plus grand (en général, 40 ou plus).
-
Les statistiques d'adéquation de l'ajustement ne sont qu'un des types de mesures permettant d'évaluer l'ajustement du modèle. Même si un modèle a une valeur souhaitable, vous devez consulter les graphiques des valeurs résiduelles pour vérifier que le modèle respecte les hypothèses.
Rigidité = 12,70 - 1,517 Densité + 0,1622 Densité^2
Récapitulatif du modèle
| S | R carré | R carré (ajust) |
|---|---|---|
| 7,56342 | 89,13% | 88,29% |
Principal résultat : R carré
Dans ces résultats, la densité du panneau de particules explique environ 89 % de la variation de rigidité des panneaux. La valeur de R2 indique que le modèle est bien ajusté aux données.
Etape 5 : Déterminer si votre modèle vérifie les hypothèses de l'analyse
Les graphiques des valeurs résiduelles permettent de déterminer si le modèle est adapté et si les hypothèses de l'analyse sont vérifiées. Si elles ne le sont pas, il se peut que le modèle ne soit pas ajusté aux données et vous devez être prudent lors de l'interprétation des résultats.
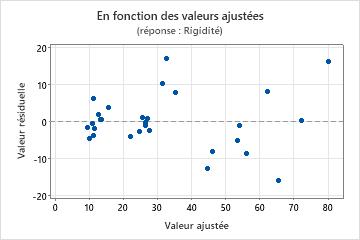
Graphique des valeurs résiduelles en fonction des valeurs ajustées
Utilisez le diagramme des valeurs résiduelles en fonction des valeurs ajustées pour vérifier l'hypothèse selon laquelle les valeurs résiduelles suivent une loi normale et ont une variance constante. Dans l'idéal, les points doivent être répartis aléatoirement des deux côtés de 0, sans schéma reconnaissable.
| Schéma | Ce que le schéma peut indiquer |
|---|---|
| Eparpillement ou répartition déséquilibrée des valeurs résiduelles en fonction des valeurs ajustées | Variance non constante |
| Curviligne | Un terme d'ordre supérieur manquant |
| Un point très éloigné de zéro | Une valeur aberrante |
| Un point éloigné des autres points dans le sens des x | Un point influent |
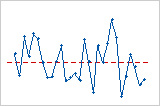
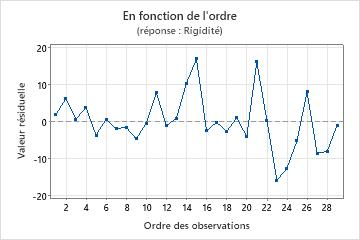
Graphique des valeurs résiduelles en fonction de l'ordre
Tendance
Décalage
Cycle
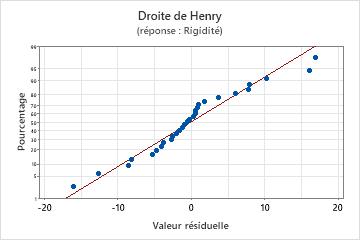
Droite de Henry
Utilisez la droite de Henry des valeurs résiduelles afin de vérifier l'hypothèse selon laquelle les valeurs résiduelles sont normalement distribuées. La droite de Henry des valeurs résiduelles doit suivre approximativement une ligne droite.
| Schéma | Ce que le schéma peut indiquer |
|---|---|
| Une ligne pas droite | Non-normalité |
| Un point éloigné de la ligne | Une valeur aberrante |
| Une modification de la pente | Une variable non identifiée |
Pour plus d'informations sur la manière de traiter les schémas dans les graphiques des valeurs résiduelles, reportez-vous à la rubrique Graphiques des valeurs résiduelles pour la fonction Droite d'ajustement.
