Un ingénieur en matériaux d'une usine fabriquant des meubles souhaite évaluer la rigidité d'un panneau de particules utilisé par l'entreprise. L'ingénieur mesure la rigidité et la densité d'un échantillon de pièces fabriquées à partir du panneau de particules.
L'ingénieur utilise une régression simple pour déterminer si la densité des particules est associée à la rigidité du panneau.
- Ouvrez les données échantillons, PanneauParticules.MWX.
- Sélectionnez .
- Dans la zone Réponse, saisissez Rigidité.
- Dans la zone Prédicteur, saisissez Densité.
- Sous Type de modèle de régression, sélectionnez Quadratique.
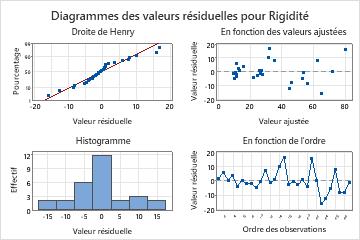
- Cliquez sur Graphiques. Sous Graphiques des valeurs résiduelles, sélectionnez Quatre en un. Cliquez sur OK.
- Cliquez sur Options. Sous Options d'affichage, sélectionnez Afficher l'intervalle de confiance et Afficher l'intervalle de prediction.
- Cliquez sur OK dans chaque boîte de dialogue.
Interpréter des résultats
Dans le tableau d'analyse de la variance, la valeur de p associée au modèle de régression est de 0,000, ce qui signifie que la véritable valeur de p est inférieure à 0,0005. La valeur de p étant inférieure au seuil de signification de 0,05, l'ingénieur peut conclure que l'association entre la rigidité et la densité est statistiquement significative. Dans le tableau d'analyse séquentielle de la variance, la valeur de p est de 0,000 pour le terme linéaire Densité et de 0,003 pour le terme quadratique Densité2. Les deux valeurs sont inférieures au seuil de signification de 0,05.
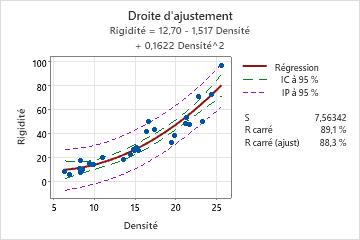
Toutefois, il semble y avoir une valeur aberrante dans le coin supérieur droit du graphique de la droite d'ajustement. Cette valeur aberrante étant susceptible d'avoir un effet important sur les résultats, l'ingénieur doit étudier ce point pour expliquer sa position.
Rigidité = 12,70 - 1,517 Densité + 0,1622 Densité^2
Récapitulatif du modèle
| S | R carré | R carré (ajust) |
|---|---|---|
| 7,56342 | 89,13% | 88,29% |
Analyse de la variance
| Source | DL | Somme des carrés | CM | F | P |
|---|---|---|---|---|---|
| Régression | 2 | 12189,4 | 6094,70 | 106,54 | 0,000 |
| Erreur | 26 | 1487,3 | 57,21 | ||
| Total | 28 | 13676,7 |
Analyse séquentielle de la variance
| Source | DL | Somme des carrés | F | P |
|---|---|---|---|---|
| Linéaire | 1 | 11552,8 | 146,86 | 0,000 |
| Quadratique | 1 | 636,6 | 11,13 | 0,003 |