Méthodes et formules pour la fonction pas à pas dans Ajuster le modèle de régression

Sélectionnez la méthode ou la formule de votre choix.

Sur ce thème

Méthode pas à pas
Procédure de sélection ascendante
Procédure d'élimination descendante
Procédure de sélection ascendante par critères d'information
Sélection ascendante avec validation

Méthode pas à pas

Permet de sélectionner les variables en supprimant des prédicteurs du modèle existant ou en en y ajoutant sur la base des résultats du test F. La méthode pas à pas combine les procédures de sélection ascendante et d'élimination descendante. La sélection pas à pas ne peut pas s'effectuer si le modèle initial utilise tous les degrés de liberté.

Variables à enlever

Minitab calcule la statistique F et la valeur de p pour chaque variable du modèle. Si le modèle contient j variables, alors pour toute variable, x_r, F est calculé comme suit :

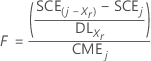
Notation

Terme	Description
SCE_{(j – X_r )}	SC Erreur pour le modèle qui ne contient pas x_r
SCE_j	SC Erreur pour le modèle qui contient x_r
CME_j	CM Erreur pour le modèle qui contient x_r

Si la valeur de p d'une variable est supérieure à la valeur indiquée dans Alpha pour exclure, Minitab supprime la variable dont la valeur de p est la plus élevée du modèle, calcule l'équation de régression, affiche les résultats et passe à l'étape suivante.

Variables à ajouter

Si Minitab ne peut pas supprimer une variable, la procédure tente d'en ajouter une. Minitab calcule la statistique F et valeur de p pour chaque variable qui n'est pas présente dans le modèle. Si le modèle contient j variables, alors, pour toute variable, x_a, F est calculé comme suit :

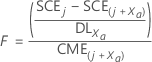
Notation

Terme	Description
SCE_j	SC Erreur avant l'ajout de x_a au modèle
SCE_(j+_{X_a )}	SC Erreur après l'ajout de x_a au modèle
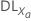	Degrés de liberté pour la variable X_a
CME_(j+_{X_a )}	CM Erreur après l'ajout de x_a au modèle

Si la valeur de p correspondant à la statistique F d'une variable est inférieure à la valeur indiquée dans Alpha pour inclure, Minitab ajoute au modèle la variable dont la valeur de p est la plus faible au modèle, calcule l'équation de régression, affiche les résultats et passe à une nouvelle étape. Lorsqu'il devient impossible d'ajouter une variable au modèle ou d'en supprimer, la procédure pas à pas se termine.

Procédure de sélection ascendante

Méthode permettant de déterminer les termes à conserver dans un modèle. La sélection ascendante ajoute des variables au modèle en utilisant la même méthode que la procédure pas à pas. Une variable n'est jamais enlevée une fois qu'elle a été ajoutée. La procédure de sélection ascendante par défaut se termine lorsqu'aucune des variables candidates n'a de valeur de p inférieure à la valeur spécifiée dans Alpha pour inclure.

Procédure d'élimination descendante

Méthode permettant de déterminer les variables à conserver dans un modèle. L'élimination descendante part d'un modèle contenant tous les termes, puis supprime des termes un par un, avec la même méthode que pour la procédure pas à pas. Aucune variable exclue ne peut être réintégrée au modèle. La procédure d'élimination descendante par défaut se termine lorsqu'aucune des variables incluses dans le modèle n'a de valeur de p supérieure à la valeur spécifiée dans Alpha pour exclure. L'élimination descendante ne peut pas s'effectuer si le modèle initial utilise tous les degrés de liberté.

Procédure de sélection ascendante par critères d'information

Méthode permettant de déterminer les variables à conserver dans un modèle. La procédure de sélection ascendante par critères d'information ajoute au modèle le terme ayant la plus faible valeur de p à chaque étape. D'autres termes peuvent être intégrés au modèle au cours d'une même étape si les paramètres de l'analyse autorisent la prise en compte des termes non hiérarchiques mais exigent que chaque modèle soit hiérarchique. Minitab calcule les critères d'information de chaque étape. Minitab affiche les résultats de l'analyse pour le modèle présentant la plus petite valeur pour le critère d'information sélectionné (AICc ou BIC). Dans la plupart des cas, la procédure continue jusqu'à ce que l'une des situations suivantes se produise :

La procédure ne trouve pas d’amélioration du critère pour 8 étapes consécutives.
La procédure ajuste le modèle complet.
La procédure ajuste un modèle qui conserve un degré de liberté pour l'erreur.

Si vous définissez des paramètres qui requièrent un modèle hiérarchique à chaque étape et qui n'autorisent l'introduction que d'un seul terme à la fois, la procédure se poursuit jusqu'à ce qu'elle ait ajusté le modèle complet ou un modèle qui conserve un degré de liberté pour l'erreur. Minitab affiche les résultats de l'analyse pour le modèle présentant la plus petite valeur pour le critère d'information sélectionné (AICc ou BIC).

Sélection ascendante avec validation

La procédure de sélection ascendante avec validation dépend de la méthode de validation.

Ensemble de données de test

Lorsque vous utilisez un ensemble de données de test, la procédure est semblable à la sélection ascendante. A chaque étape, Minitab ajoute le terme avec la plus petite valeur de p au modèle. A la fin de chaque étape, Minitab calcule la valeur de R² de test. A la fin de la procédure de sélection ascendante, le modèle ayant la valeur de R² de test la plus élevée correspond au modèle final.

La procédure ajoute des termes jusqu'à ce que l'une des conditions suivantes se produise :

La procédure ne trouve pas d'amélioration dans le critère pour 8 étapes consécutives.
La procédure correspond au modèle complet.
La procédure correspond à un modèle qui laisse un degré de liberté pour l'erreur.

Validation croisée sur K partitions

Avec la validation croisée, la procédure répète la sélection ascendante pour chaque ensemble. La sélection ascendante se poursuit sur le premier ensemble pendant 16 étapes sans amélioration de la somme des carrés pour l'erreur. Pour chaque ensemble restant, la sélection ascendante se poursuit jusqu'à ce que la procédure atteigne le minimum des nombres suivants :

Le nombre d'étapes d'une partition précédente
16 étapes sans amélioration de la somme des carrés pour l'erreur
Le nombre d'étapes pour ajuster le modèle complet
Le nombre d'étapes pour ajuster un modèle qui laisse 1 degré de liberté pour l'erreur

Une fois les procédures de sélection ascendante terminées pour chaque ensemble, Minitab calcule les valeurs globales de R² pas à pas de K ensembles pour chaque étape de la procédure de sélection pour chaque ensemble. L'étape avec la valeur de R² pas à pas de K ensembles devient l'étape pour le modèle choisi à partir d'une procédure finale de sélection ascendante.

Enfin, Minitab effectue la sélection ascendante sur l'ensemble complet de données. Minitab affiche les résultats de la régression pour le modèle à l'étape avec la valeur globale maximale de R² pas à pas de K ensembles des procédures de pas à pas de K ensembles. Le tableau des détails pour la sélection du modèle et le graphique du R² pas à pas de K ensembles par rapport à l'étape de sélection du modèle se poursuivent pendant 8 étapes après l'étape des résultats de la régression.