Sur ce thème
Régression pondérée
La régression par les moindres carrés pondérée est une méthode permettant de traiter les observations qui présentent des variances non constantes. Si les variances ne sont pas constantes, attribuez :
- des pondérations relativement faibles aux observations ayant des variances importantes
- des pondérations relativement importantes aux observations ayant des variances faibles
Les pondérations sont généralement choisies comme l'inverse de la variance de l'erreur pure dans le réponse.
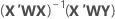
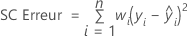
Notation
| Terme | Description |
|---|---|
| X | matrice du plan |
| X' | transposition de la matrice de plan |
| W | matrice n x n, avec les pondérations sur la diagonale |
| Y | vecteur des valeurs de réponse |
| n | nombre d'observations |
| wi | pondération pour l'ie observation |
| yi | valeur de réponse pour l'ie observation |
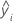 | valeur ajustée pour l'ie observation |
Transformation de Box-Cox
La transformation de Box-Cox sélectionne les valeurs lambda (comme indiqué ci-dessous) qui minimisent la somme des carrés des valeurs résiduelles. La transformation obtenue est Y λ lorsque λ ≠ 0, et ln(Y) lorsque λ = 0. Lorsque λ < 0, Minitab multiplie également la réponse transformée par −1 pour conserver l'ordre de la réponse non transformée.
Minitab recherche une valeur optimale entre −2 et 2. Les valeurs en dehors de cet intervalle sont susceptibles de ne pas fournir un meilleur ajustement.
Voici quelques transformations courantes dans lesquelles Y′ représente la transformation des données Y :
| Valeur lambda (λ) | Transformation |
|---|---|
| λ = 2 | Y′ = Y 2 |
| λ = 0,5 | Y′ = 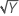 |
| λ = 0 | Y′ = ln(Y ) |
| λ = −0,5 |  |
| λ = −1 | Y′ = −1 / Y |
Équation de régression
Pour un modèle avec plusieurs prédicteurs, l’équation est la suivante :
y = β0 + β1x1 + ... + βkxk + ε
L’équation ajustée est :
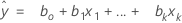
Dans la régression linéaire simple, qui n’inclut qu’un seul prédicteur, le modèle est :
y=ß0+ ß1x1+ε
En utilisant des estimations de régression b0 pour ß0, et b1 pour ß1, l’équation ajustée est la suivante :
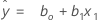
Équations avec une variable catégorielle
- Équation séparée de chaque ensemble de niveaux prédicteurs catégoriels
- Equation unique
- C1
- La variable de réponse
- C2
- Un prédicteur continu
- C3
- Une variable prédictive catégorique avec les niveaux Rouge et Bleu
- Bleu: C1 = 0,184 + 0,1964*C2
- Rouge: C1 = 0,011 + 0,1964*C2
Une seule équation utilise une variable indicatrice pour représenter la variable catégorique.
C1 = 0,184 + 0,1964*C2 + 0,0*C3_Bleu - 0,173*C3_Rouge
- Observation bleue (C3_Bleu = 1, C3_Rouge = 0) : C1 = 0,184 + 0,1964*C2 + 0,0*1 - 0,173*0 = 0,184 + 0,1964*C2
- Observation rouge (C3_Bleu = 0, C3_Rouge = 1 : C1 = 0,084 + 0,1964*C2 + 0,0*0 - 0,173*1 = 0,011 + 0,1964*C2
Notation
| Terme | Description |
|---|---|
| y | réponse |
| xk | Ktrimestre . Chaque terme peut être un prédicteur unique, un terme polynomial ou un terme d’interaction. |
| ßk | kième coefficient de régression de population |
| ε | terme d’erreur qui suit une distribution normale avec une moyenne de 0 |
| bk | Estimation du kième coefficientde régression de la population |
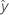 | réponse ajustée |
Matrice du plan
La matrice du plan contient les prédicteurs dans une matrice (X) de n lignes, où n correspond au nombre d'observations. Il existe une colonne pour chaque coefficient du modèle.
Les prédicteurs de catégories sont codés à l'aide du codage 1, 0 ou -1, 0, 1. X n'inclut pas de colonne pour le niveau de référence du facteur.
Pour calculer les colonnes d'un terme d'interaction, multipliez toutes les valeurs correspondantes des prédicteurs dans l'interaction. Par exemple, supposons que la première observation a une valeur de 4 pour le prédicteur A et une valeur de 2 pour le prédicteur B. Dans la matrice du plan, l'interaction entre A et B est représentée par le chiffre 8 (4 x 2).
Inverse de x'x
Procédure pour supprimer des prédicteurs fortement corrélés de l'équation de régression dans Ajuster le modèle de régression
Supposons que rij est l'élément dans la matrice de balayage associé à Xi et Xj.
Les variables sont saisies ou supprimées une à une. Xk est éligible à la saisie s'il correspond à une variable indépendante ne se trouvant pas actuellement dans le modèle avec rkk ≥ 1 (tolérance avec une valeur par défaut de 0,0001) et également pour chaque variable Xj se trouvant actuellement dans le modèle,
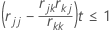
- Minitab exécute la méthode SWEEP sur la matrice de corrélation, R, traitant X1 … Xp comme s'il s'agissait de variables aléatoires.
- Pour tout prédicteur continu, Minitab compare l'élément rkk avec la tolérance ; rkk ≥ tolérance, où k = 1 par rapport à p.
- Pour chaque variable Xj se trouvant actuellement dans le modèle, Minitab vérifie que (rjj – rjk * (rkj / rkk)) * tolérance ≤ 1.
Remarque
Où rkk, rjk, rjj sont les éléments de diagonale et hors diagonale correspondant aux variables Xj et Xk après l'étape k des opérations SWEEP.
- Dans le cas contraire, le prédicteur échoue au test et est supprimé du modèle.
Remarque
La valeur de tolérance par défaut est de 8,8e-12.
Remarque
Vous pouvez utiliser la sous-commande TOLERANCE avec la session de commande REGRESS pour forcer Minitab à conserver dans le modèle un prédicteur fortement corrélé avec un autre prédicteur. Cependant, diminuer la tolérance peut s'avérer dangereux, car cela peut générer des résultats imprécis sur le plan numérique.
