Sur ce thème
Valeur ajustée
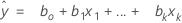
Notation
| Terme | Description |
|---|---|
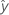 | valeur ajustée |
| xk | ke terme. Chaque terme peut être un prédicteur unique, un terme polynomial ou un terme d'interaction. |
| bk | estimation du ke coefficient de régression |
Erreur type de la valeur ajustée (ErT ajust)
L'erreur type de la valeur ajustée dans un modèle de régression avec un prédicteur est calculée comme suit :

L'erreur type de la valeur ajustée dans un modèle de régression avec plusieurs prédicteurs est calculée comme suit :

Pour la régression pondérée, inclure la matrice de poids dans l’équation:

Lorsque les données disposent d’un ensemble de données de test ou d’une validation croisée Buplé, les formules sont les mêmes. La valeur de s2 provient des données de formation. La matrice de conception et la matrice de poids proviennent également des données de formation.
Notation
| Terme | Description |
|---|---|
| s2 | mean square error |
| n | number of observations |
| x0 | new value of the predictor |
 | mean of the predictor |
| xi | ie predictor value |
| x0 | vector of values that produce the fitted values, one for each column in the design matrix, beginning with a 1 for the constant term |
| X0 | transpose of the new vector of predictor values |
| X | design matrix |
| W | weight matrix |
Intervalle de confiance pour une valeur ajustée (IC)
Formule
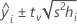
Pour la régression pondérée, la formule comprend les pondérations :
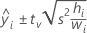
où tv est le 1–α/2 quantile de la distribution t avec v degrés de liberté pour un intervalle bilatéral. Pour une limite unilatérale, tv est le 1–α quantile de la distribution t avec v degrés de liberté.
Lorsque vous utilisez un ensemble de données de test ou une validation croisée de K ensembles, les degrés de liberté et l'erreur quadratique moyenne proviennent de l'ensemble de données d'apprentissage.
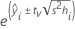
Notation
| Terme | Description |
|---|---|
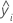 | fitted value |
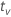 | quantile from the t distribution |
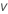 | degrees of freedom |
 | mean square error |
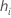 | leverage for the ie observation |
| wi | weight for the ie observation |
Valeurs résiduelles
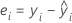
Notation
| Terme | Description |
|---|---|
| yi | ie valeur de réponse observée |
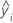 | ie valeur ajustée pour la réponse |
Valeur résiduelle normalisée (Val. résid. norm)
Les valeurs résiduelles normalisées sont également appelées "valeurs résiduelles studentisées en interne".
Formule

Notation
| Terme | Description |
|---|---|
| ei | ie valeur résiduelle |
| hi | ie élément sur la diagonale de X(X'X)–1X' |
| s2 | carré moyen de l'erreur |
| X | matrice du plan |
| X' | transposition de la matrice de plan |
Valeurs résiduelles normalisées (Val. résid. norm.) avec validation
Formule

Pour la régression pondérée, la formule comprend la pondération :
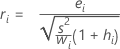
Notation
| Terme | Description |
|---|---|
| ei | ie residual in the validation data set |
| hi | leverage for the ie validation row |
| s2 | mean square error for the training data set |
| wi | weight for the ie observation in the validation data set |
Valeurs résiduelles supprimées (studentisées)
Egalement appelées valeurs résiduelles studentisées de manière externe. La formule estla suivante :
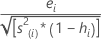
Voici une autre présentation possible de la formule :

Le modèle qui effectue l'estimation de l'ie observation omet cette dernière dans l'ensemble de données. Par conséquent, l'ie observation ne peut pas influencer l'estimation. Chaque valeur résiduelle supprimée suit une loi de Student avec 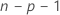 degrés de liberté.
degrés de liberté.
Notation
| Terme | Description |
|---|---|
| ei | ie valeur résiduelle |
| s(i)2 | carré moyen de l'erreur calculé sans l'ie observation |
| hi | ie élément sur la diagonale de X(X'X)–1X' |
| n | nombre d'observations |
| p | nombre de termes, constante incluse |
| SCE | somme des carrés de l'erreur |
