Sur ce thème
Effets de levier (Hi)
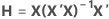
L'effet de levier de la ie observation est le ie élément diagonal, hi de H. Si la valeur de hi est élevée, la ie observation contient des prédicteurs aberrants (X1i, X2i, ..., Xpi). En d'autres termes, les valeurs de prédicteurs sont éloignées du vecteur de moyenne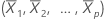
, avec distance de Mahalanobis.
Les valeurs à effet de levier sont comprises entre 0 et 1. Dans le tableau des observations aberrantes, Minitab affecte un X aux observations qui présentent soit des effets de levier supérieurs à 3 p/n soit la valeur 0,99, en considérant en priorité la plus petite de ces valeurs. Généralement, vous examinez des valeurs à fort effet de levier.
Notation
| Terme | Description |
|---|---|
| X | matrice du plan |
| hi | ie élément sur la diagonale de la matrice H |
| p | nombre de termes dans le modèle, constante incluse |
| n | nombre d'observations |
Effets de levier (Hi) avec validation
Formule
Pour la régression pondérée, la formule comprend la pondération :
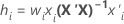
Notation
| Terme | Description |
|---|---|
| X | design matrix for the rows in the training data set or the folds that act as the training data set |
| xi | the vector of predictors in the ie validation row |
| wi | weight for the ie validation row |
Distance de Cook
Mesure globale, D, de l'impact combiné dans tous les coefficients de régression estimés sur une observation. Minitab calcule D à l'aide des valeurs à effet de levier et des valeurs résiduelles normalisées, puis détermine si une observation est aberrante à la fois au regard des valeurs de X et de Y. Les observations dont les valeurs de D sont élevées peuvent être des valeurs aberrantes.
Formule
La distance de Cook est la distance entre les coefficients calculés avec et sans l'ie observation. Minitab calcule la distance de Cook sans ajuster de nouvelle équation de régression à chaque fois qu'une observation est omise. Le calcul est le suivant :
Notation
| Terme | Description |
|---|---|
| ei | ie valeur résiduelle |
| hi | ie élément sur la diagonale de  |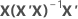
| p | nombre de paramètres de modèle, constante incluse |
| s 2 | carré moyen de l'erreur |
| b | vecteur de coefficients |
| b(i) | vecteur de coefficients calculé après la suppression de l'ie observation |
| X | matrice du plan |
DFITS
Combine l'effet de levier et les valeurs résiduelles studentisées pour fournir une mesure globale du caractère aberrant d'une observation. DFITS mesure l'influence de chaque observation sur les valeurs ajustées dans un modèle de régression et d'ANOVA. Les observations présentant des valeurs DFITS élevées peuvent être des valeurs aberrantes.
DFITS exprime approximativement le changement, en nombre d'écarts types, de la valeur ajustée lorsque chaque observation est supprimée de l'ensemble de données et que le modèle est réajusté. Minitab peut également calculer la valeur DFITS sans ajuster de nouvelle équation de régression à chaque fois qu'une observation est omise.
Formule
Notation
| Terme | Description |
|---|---|
| ei | ie valeur résiduelle |
| hi | ie élément sur la diagonale de  |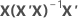
| X | matrice du plan |
 | ie réponse ajustée |
 | valeur ajustée calculée sans l'ie observation |
| CME (i) | carré moyen de l'erreur calculé sans l'ie observation |
| n | nombre d'observations |
| p | nombre de paramètres de modèle |
Facteurs d'inflation de la variance (FIV)
Le FIV peut être obtenu en faisant régresser chaque prédicteur sur les prédicteurs restants et en notant la valeur R2.
Formule
Pour le prédicteur xj, le FIV est le suivant :
Notation
| Terme | Description |
|---|---|
| R2( xj) | coefficient de détermination avec xj comme variable de réponse et autres termes du modèle comme prédicteurs |
Statistique de Durbin-Watson
Teste la présence d'une autocorrélation dans les valeurs résiduelles en déterminant si la corrélation entre deux termes d'erreur adjacents est égale à zéro. Le test repose sur l'hypothèse que les erreurs sont générées par un processus d'autorégression de premier ordre. Minitab suppose que les observations présentent un ordre significatif, tel qu'un ordre temporel.
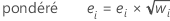
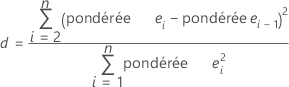
Notation
| Terme | Description |
|---|---|
| ei | Ie valeur résiduelle |
| ei -1 | valeur résiduelle pour l'observation précédente |
| n | nombre d'observations |
