Sur ce thème
Somme des carrés (SomCar)
Pour les matrices, voici les formules pour les différentes sommes des carrés :

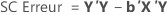
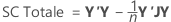
Minitab décompose la composante de la somme des carrés de la régression ou des traitements en indiquant la proportion de variation expliquée par chaque terme, en utilisant à la fois la somme des carrés séquentielle et la somme des carrés ajustée.
Notation
| Terme | Description |
|---|---|
| b | vecteur des coefficients |
| X | matrice du plan |
| Y | vecteur des valeurs de réponse |
| n | nombre d'observations |
| J | matrice n sur n de 1s |
Somme des carrés séquentielle
Minitab répartit la composante de variance de la somme des carrés de la régression ou des traitements en sommes des carrés séquentielles pour chaque facteur. La somme des carrés séquentielle dépend de l'ordre dans lequel les facteurs ou les prédicteurs sont entrés dans le modèle. La somme des carrés séquentielle est la part de la somme des carrés de la régression expliquée par un facteur unique, en tenant compte de tous les autres facteurs déjà entrés.
Par exemple, dans le cas d'un modèle possédant trois facteurs ou prédicteurs X1, X2 et X3, la somme des carrés séquentielle pour X2 indique la proportion de la variation restante expliquée par X2, sachant que X1 figure déjà dans le modèle. Pour obtenir une séquence de facteurs différente, répétez l'analyse et entrez les facteurs dans un autre ordre.
Degrés de liberté (DL)
Les degrés de liberté pour chaque composant du modèle sont les suivants :
| Sources de variation | DL |
|---|---|
| Régression | p |
| Erreur | n – p – 1 |
| Total | n – 1 |
- Les données contiennent plusieurs observations avec les mêmes valeurs de prédicteurs.
- Les données contiennent les points corrects pour estimer les termes supplémentaires absents du modèle.
Notation
| Terme | Description |
|---|---|
| n | nombre d'observations |
| p | nombre de coefficients du modèle, indépendamment de la constante |
CM ajust - Régression
La formule du carré moyen (CM) de la régression est la suivante :
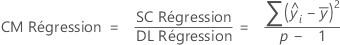
Notation
| Terme | Description |
|---|---|
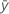 | réponse moyenne |
 | ie réponse ajustée |
| p | nombre de termes dans le modèle |
CM ajust - Erreur
Le carré moyen de l'erreur (également abrégé en CM Erreur ou CME et noté s2) est la variance autour de la droite de régression. La formule est la suivante :

Notation
| Terme | Description |
|---|---|
| yi | ie valeur de réponse observée |
 | ième réponse ajustée |
| n | nombre d'observations |
| p | nombre de coefficients dans le modèle, constante non incluse |
CM ajust - Total
La formule pour le carré moyen (CM) total est la suivante :

Notation
| Terme | Description |
|---|---|
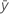 | réponse moyenne |
| yi | ie valeur de réponse observée |
| n | nombre d'observations |
Valeur F
Les formules pour les statistiques F sont les suivantes :
- F(Régression)
-

- F(Terme)
-

- F(Inadéquation de l'ajustement)
-

Notation
| Terme | Description |
|---|---|
| CM Régression | Mesure de la variation de la réponse expliquée par le modèle actuel. |
| CM Erreur | Mesure de la variation que le modèle n'explique pas. |
| CM Terme | Mesure de l'ampleur de la variation expliquée par un terme après la prise en compte des autres termes du modèle. |
| CM Inadéquation de l'ajustement | Mesure de la variation de la réponse qui peut être modélisée en ajoutant d'autres termes au modèle. |
| CM Erreur pure | Mesure de la variation dans les données de réponse répétées. |
Valeur de p - Tableau d'analyse de la variance
La valeur de p est une probabilité calculée à partir d'une loi F avec les degrés de liberté (DL) suivants :
- DL en numérateur
- somme des degrés de liberté pour le ou les termes du test
- DL en dénominateur
- degrés de liberté pour l'erreur
Formule
1 − P(F ≤ fj)
Notation
| Terme | Description |
|---|---|
| P(F ≤ f) | fonction de répartition de la loi F |
| f | statistique f pour le test |
Test d'inadéquation de l'ajustement pour l'erreur pure
- La somme des écarts quadratiques de la réponse par rapport à la moyenne dans chaque ensemble de répliques, puis les additionne afin d'obtenir la somme des carrés pour l'erreur pure (SC EP).
- Le carré moyen de l'erreur pure


où n est le nombre d'observations et m le nombre de combinaisons de niveaux x distinctes
- La somme des carrés pour l'inadéquation de l'ajustement

- Le carré moyen pour l'inadéquation de l'ajustement

- Les statistiques de test

Des valeurs de F élevées et de faibles valeurs de p suggèrent que le modèle est inadapté.
Valeur de p - Test d'inadéquation de l'ajustement
- DL en numérateur
- degrés de liberté pour l'inéquation de l'ajustement
- DL en dénominateur
- degrés de liberté pour l'erreur pure
Formule
1 − P(F ≤ fj)
Notation
| Terme | Description |
|---|---|
| P(F ≤ fj) | fonction de répartition de la loi F |
| fj | statistique f pour le test |
