Méthodes dans Ajuster le modèle de Poisson

L'extension des modèles linéaires classiques aux modèles linaires généralisés se compose de deux parties : une loi issue de la famille exponentielle et une fonction de liaison.

Famille exponentielle

La première partie étend le modèle linéaire aux variables de réponse membres d'une grande famille de lois appelée famille exponentielle. Le format général des fonctions de répartition de probabilités pour les membres de la famille exponentielle de lois est le suivant :

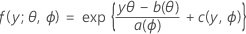
où a(∙), b(∙) et c(∙) dépendent de la loi de la variable de réponse. Le paramètre θ est un paramètre d'emplacement souvent appelé paramètre canonique et ϕ est un paramètre de dispersion. La fonction a(ϕ) a habituellement la forme a(ϕ) = ϕ/ω, où ω représente une constante ou une pondération connue susceptible de varier d'une observation à l'autre. (Dans Minitab, lorsque les pondérations sont indiquées, la fonction a(ϕ) est ajustée en conséquence.)

Les membres de la famille exponentielle peuvent être des lois de probabilité discrète ou des lois de distribution continue. Les lois de distribution continue membres de la famille exponentielle comprennent entre autres la loi normale et la distribution gamma. Les lois de probabilité discrète membres de la famille exponentielle incluent la loi binomiale et la loi de Poisson. Le tableau suivant présente les caractéristiques de certaines de ces lois.

Loi de distribution	ϕ	b(θ)	a(φ)	c(y, ϕ)
Normale	σ2	θ2/2	φω
Binomiale	1		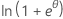φ/ω	-ln(y!)
Poisson	1	exp(θ)	φ/ω

Fonction de liaison

La seconde partie est la fonction de liaison. Elle associe la moyenne de la réponse dans la i^e observation à un prédicteur linéaire de cette manière :

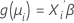
Le modèle linéaire classique est un cas particulier de cette formulation générale dans laquelle la fonction de liaison est la fonction d'identité.

Le choix de la fonction de liaison dans la seconde partie dépend de la loi de la famille exponentielle dans la première partie. Chaque loi de la famille exponentielle dispose d'une fonction de liaison particulière appelée fonction de liaison canonique. Cette dernière vérifie l'équation g (μ_i) = X_i'β = θ, où θ est le paramètre canonique. La fonction de liaison canonique engendre des propriétés statistiques voulues du modèle. Les statistiques d'adéquation de l'ajustement peuvent servir à comparer les ajustements obtenus par différentes fonctions de liaison. Le choix de certaines fonctions de liaison peut dépendre de raisons historiques ou de leur signification particulière dans une discipline. Par exemple, la fonction logit a pour avantage de fournir une estimation des rapports de probabilités de succès. Nous pouvons également prendre comme exemple la fonction de liaison normit, qui suppose qu'il existe une variable sous-jacente suivant une loi de distribution normale et classée en catégories binaires.

Minitab offre trois fonctions de liaison pour chaque classe de modèles. Les différentes fonctions de liaison permettent de trouver des modèles bien ajustés à une grande variété de données.

Pour les modèles binomiaux, les fonctions de liaison sont logit, normit (également appelée probit) et gompit (appelée également log-log complémentaire). Ces fonctions sont l'inverse de la loi de distribution logistique standard cumulée (logit), l'inverse de la loi de distribution normale standard cumulée (normit) et l'inverse de la loi de distribution de Gompertz (gompit). Logit représente la fonction de liaison canonique pour les modèles binoniaux, ce qui en fait la fonction de liaison par défaut.

Pour les modèles de Poisson, les fonctions de liaison sont le logarithme népérien, la racine carrée et l'identité. Le logarithme népérien représente la fonction de liaison canonique pour les modèles de Poisson, ce qui en fait la fonction de liaison par défaut.

Les fonctions de liaison sont récapitulées ci-après :

Modèle	Nom	Fonction de liaison, g(μi)
Binomiale	logit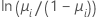
Binomiale	normit (probit)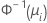
Binomiale	gompit (log-log complémentaire)
Poisson	logarithme népérien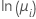
Poisson	racine carrée
Poisson	identité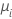

Notation

Terme	Description
μi	réponse moyenne de la ie ligne
g(μi)	fonction de liaison
X	vecteur de variables de prédiction
β	vecteur des coefficients associés aux prédicteurs
	inverse de la fonction de répartition cumulée pour la loi normale

Décrit un ensemble unique de valeurs de facteurs/covariables dans un fichier de données. Minitab calcule les probabilités d'événements, les valeurs résiduelles et d'autres mesures de diagnostic pour chaque combinaison de facteurs/covariables.

Par exemple, si un fichier de données inclut des facteurs relatifs au sexe et à l'origine ethnique et la covariable relative à l'âge, la combinaison de ces prédicteurs peut contenir autant de combinaisons de covariables que de sujets. Si un fichier de données inclut uniquement les facteurs relatifs au sexe et à l'origine ethnique, les deux étant codés à deux niveaux, il existe seulement quatre combinaisons de facteurs/covariables possibles. Si vous saisissez les données comme des effectifs (ou des réussites, des essais ou des échecs), chaque ligne contient une combinaison de facteurs/covariables.