Sur ce thème
R carré de la somme des carrés d'écart
Le R2 de la somme des carrés d'écart est généralement considéré comme la proportion de la somme totale des carrés des écarts de la variable de réponse que le modèle explique.
Interprétation
Plus le R2 de la somme des carrés d'écart est élevé, plus le modèle est ajusté à vos données. Le R2 de la somme des carrés d'écart est toujours compris entre 0 et 100 %.
Le R2 de la somme des carrés d'écart augmente toujours lorsque vous ajoutez des termes à un modèle. Par exemple, le meilleur modèle à 5 termes aura toujours une valeur R2 au moins aussi élevée que celle du meilleur modèle à 4 termes. Par conséquent, le R2 de la somme des carrés d'écart est surtout utile pour comparer des modèles de même taille.
Les statistiques d'adéquation de l'ajustement ne sont qu'un des types de mesures permettant d'évaluer l'ajustement du modèle. Même si un modèle présente une valeur souhaitée, vous devez consulter les graphiques des valeurs résiduelles et les tests d'adéquation de l'ajustement pour évaluer l'ajustement du modèle aux données.
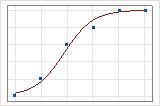
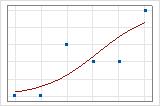
Vous pouvez utiliser une droite d'ajustement pour illustrer graphiquement différentes valeurs de R2 de la somme des carrés d'écart. Le premier diagramme illustre un modèle qui explique environ 96 % de la somme des carrés d'écart de la réponse. Le second diagramme illustre un modèle qui explique environ 60 % de la somme des carrés d'écart de la réponse. Plus un modèle explique la somme des carrés d'écart, plus les points de données sont proches de la courbe. En théorie, si un modèle pouvait expliquer 100 % de la somme des carrés d'écart, les valeurs ajustées seraient toujours égales aux valeurs observées et tous les points de données se situeraient sur la courbe.
La disposition des données a un impact sur le R2 de la somme des carrés d'écart. Le R2 de la somme des carrés d'écart est généralement plus élevé pour des données avec plusieurs essais par ligne que pour des données avec un seul essai par ligne. Les R2 de la somme des carrés d'écart sont comparables uniquement entre des modèles qui utilisent le même format de données. Pour plus d'informations, reportez-vous à la rubrique Influence du format des données sur l'ajustement dans la régression logistique binaire.
R carré (ajust) de la somme des carrés d'écart
Le R2 ajusté de la somme des carrés d'écart est la proportion de la somme des carrés d'écart de la réponse qui est expliquée par le modèle, ajustée au nombre de prédicteurs du modèle par rapport au nombre d'observations.
Interprétation
Pour comparer des modèles n'ayant pas le même nombre de termes, utilisez le R2 ajusté de la somme des carrés d'écart. Celui-ci augmente toujours lorsque vous ajoutez un terme au modèle. Le R2 ajusté de la somme des carrés d'écart intègre le nombre de termes dans le modèle pour vous aider à choisir le modèle correct.
| Etape | % de pomme de terre | Vitesse de refroidissement | Température de cuisson | R2 de la somme des carrés d'écart | R2 ajusté de la somme des carrés d'écart | Valeur de p |
|---|---|---|---|---|---|---|
| 1 | X | 52% | 51% | 0,000 | ||
| 2 | X | X | 63% | 62% | 0,000 | |
| 3 | X | X | X | 65% | 62% | 0,000 |
La première étape génère un modèle de régression statistiquement significatif. La deuxième étape, qui ajoute la vitesse de refroidissement au modèle, augmente le R2 ajusté de la somme des carrés d'écart, ce qui indique que la vitesse de refroidissement améliore le modèle. La troisième étape, qui ajoute la température de cuisson au modèle, augmente le R2 de la somme des carrés d'écart, mais pas le R2 ajusté de la somme des carrés d'écart. Ces résultats indiquent que la température de cuisson n'améliore pas le modèle. Selon ces résultats, vous devriez supprimer la température de cuisson du modèle.
La disposition des données a une incidence sur le R2 ajusté de la somme des carrés d'écart. Pour les mêmes données, le R2 ajusté de la somme des carrés d'écart est généralement plus élevé pour des données avec plusieurs essais par ligne que pour des données avec un seul essai par ligne. Utilisez le R2 ajusté de la somme des carrés d'écart uniquement pour comparer l'ajustement des modèles ayant le même format de données. Pour plus d'informations, accédez à Influence du format des données sur l'ajustement dans la régression logistique binaire.
R carré de la somme des carrés des écarts de test
Interprétation
Utilisez le R2 de la somme des carrés des écarts de test pour déterminer dans quelle mesure votre modèle correspond aux nouvelles données. Les modèles dont les valeurs de R2 de la somme des carrés des écarts de test sont plus grandes ont tendance à être plus performants avec de nouvelles données. Vous pouvez utiliser le R2 de la somme des carrés des écarts de test pour comparer les performances de différents modèles.
Un R2 de la somme des carrés des écarts de test sensiblement inférieur au R2 de la somme des carrés des écarts peut indiquer que le modèle est sur-ajusté. Un modèle est sur-ajusté si vous ajoutez des termes correspondant à des effets qui ne sont pas importants dans la population. Le modèle devient adapté aux données d’apprentissage et, par conséquent, peut ne pas être utile pour faire des prédictions sur la population.
Par exemple, un analyste d’une société de conseil financier élabore un modèle pour prédire les conditions futures du marché. Le modèle semble prometteur car son R2 est de 87 %. Cependant, le R2 de la somme des carrés des écarts de test est de 52 %, ce qui indique que le modèle peut être sur-ajusté.
Une valeur de R2 de la somme des carrés des écarts de test élevée n’indique pas en soi que le modèle répond à ses hypothèses. Vous devez vérifier les diagrammes des valeurs résiduelles pour vérifier les hypothèses.
R carré de la somme des carrés des écarts sur K partitions
Le R2 de la somme des carrés des écarts sur K partitions est généralement considéré comme la proportion de la somme totale des carrés des écarts dans la variable de réponse des données de validation que le modèle explique.
Interprétation
Utilisez le R2 de la somme des carrés des écarts sur K partitions pour déterminer dans quelle mesure votre modèle correspond aux nouvelles données. Les modèles dont les valeurs de R2 de la somme des carrés des écarts sur K partitions sont plus grandes ont tendance à être plus performants avec de nouvelles données. Vous pouvez utiliser les valeurs du R2 de la somme des carrés des écarts sur K partitions pour comparer les performances de différents modèles.
Un R2 de la somme des carrés des écarts sur K partitions sensiblement inférieur au R2 de la somme des carrés des écarts peut indiquer que le modèle est sur-ajusté. Un modèle est sur-ajusté si vous ajoutez des termes correspondant à des effets qui ne sont pas importants dans la population. Le modèle devient adapté à l'ensemble des données d'apprentissage et, par conséquent, peut ne pas être utile pour faire des prédictions sur la population.
Par exemple, un analyste d'une société de conseil financier élabore un modèle pour prédire les conditions futures du marché. Le modèle semble prometteur car son R2 de la somme des carrés des écarts est de 87 %. Cependant, le R2 de la somme des carrés des écarts sur K partitions est de 52 %, ce qui indique que le modèle peut être sur-ajusté.
Une valeur de R2 de la somme des carrés des écarts sur K partitions élevée n'indique pas en soi que le modèle répond à ses hypothèses. Vous devez vérifier les diagrammes des valeurs résiduelles pour vérifier les hypothèses.
AIC, AICc et BIC
Le critère d'information d'Akaike (AIC), le critère d'information d'Akaike corrigé (AICc) et le critère d'information bayésien (BIC) sont des mesures de la qualité relative d'un modèle qui rend compte de l'ajustement du modèle et du nombre de termes qu'il contient.
Interprétation
- AICc et AIC
- Lorsque l'effectif d'échantillon est relativement faible par rapport au nombre de paramètres dans le modèle, l'AICc offre de meilleurs résultats que l'AIC. L'AICc est une meilleure option car, avec des échantillons relativement petits, l'AIC tend à être faible pour les modèles qui incluent trop de paramètres. Généralement, ces deux statistiques donnent des résultats similaires quand l'effectif d'échantillon est suffisamment élevé par rapport au nombre de paramètres dans le modèle.
- AICc et BIC
- Les valeurs AICc et BIC évaluent toutes deux la probabilité du modèle, puis ajoutent une pénalité pour l'ajout de termes. Cette pénalité réduit la tendance du système à surajuster le modèle aux données échantillons. Cette réduction permet généralement de produire un modèle qui fonctionne mieux.
