Un ingénieur qualité souhaite étudier deux types de défauts dans des pièces moulées en résine : la décoloration et les agrégats. La présence d'agents contaminants dans les tuyaux flexibles et l'abrasion des pastilles de résine peuvent causer des stries d'aspect décoloré sur le produit fini. Des agrégats peuvent apparaître lorsque le procédé est réalisé avec des températures plus élevés et des vitesses de transfert plus rapides. L'ingénieur identifie trois variables de prédicteurs possibles pour les réponses (défauts). L'ingénieur note le nombre de défauts de chaque type rencontré au cours de sessions d'une heure, tout en faisant varier les niveaux des prédicteurs.
L'ingénieur souhaite étudier l'effet de plusieurs prédicteurs sur les défauts de décoloration des pièces en résine. La variable de réponse indiquant le nombre d'occurrences d'un événement dans un espace d'observation fini, il ajuste un modèle de Poisson.
- Entrez les données échantillons, DéfautsRésine.MTW.
- Sélectionnez .
- Dans la zone Réponse, saisissez "Défauts décoloration".
- Dans la zone Prédicteurs continus, saisissez ''Heures depuis nettoyage" Température.
- Dans la zone Prédicteurs de catégorie, saisissez "Taille de vis".
- Cliquez sur Graphiques.
- Dans Valeurs résiduelles des graphiques, sélectionnez Normalisé.
- Sous Graphiques des valeurs résiduelles, sélectionnez Quatre en un.
- Cliquez sur OK dans chaque boîte de dialogue
Interpréter des résultats
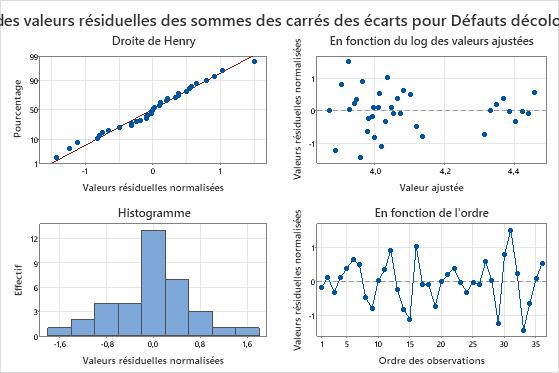
Le diagramme des valeurs résiduelles de la somme des carrés d'écart normalisée en fonction des valeurs ajustées présente une courbe distincte. Dans le diagramme des valeurs résiduelles en fonction de l'ordre, les valeurs résiduelles situées au centre sont globalement plus élevées que les valeurs résiduelles situées au début et à la fin du fichier de données. Pour ces données, les deux schémas sont dus à un terme d'interaction manquant entre la taille de la vis et la température. Le schéma est visible sur le diagramme des valeurs résiduelles en fonction de l'ordre, car l'ingénieur n'a pas collecté les données dans un ordre aléatoire. L'ingénieur réajuste le modèle avec l'interaction entre la température et la taille de la vis pour modéliser les défauts de manière plus précise.
Méthode
| Fonction de liaison | Logarithme népérien |
|---|---|
| Codage des prédicteurs de catégorie | (1; 0) |
| Lignes utilisées | 36 |
Equation de régression
| Défauts décoloration | = | exp(Y') |
|---|
| Taille de vis | |||
|---|---|---|---|
| grande | Y' | = | 4,398 + 0,01798 Heures depuis nettoyage - 0,001974 Température |
| petite | Y' | = | 4,244 + 0,01798 Heures depuis nettoyage - 0,001974 Température |
Coefficients
| Terme | Coeff | Coef ErT | Valeur de Z | Valeur de p | FIV |
|---|---|---|---|---|---|
| Constante | 4,3982 | 0,0628 | 70,02 | 0,000 | |
| Heures depuis nettoyage | 0,01798 | 0,00826 | 2,18 | 0,029 | 1,00 |
| Température | -0,001974 | 0,000318 | -6,20 | 0,000 | 1,00 |
| Taille de vis | |||||
| petite | -0,1546 | 0,0427 | -3,62 | 0,000 | 1,00 |
Récapitulatif du modèle
| R carré de la somme des carrés des écarts | R carré (ajust) de la somme des carrés des écarts | AIC | AICc | BIC |
|---|---|---|---|---|
| 64,20% | 60,80% | 253,29 | 254,58 | 259,62 |
Tests d'adéquation de l'ajustement
| Test | DL | Estimation | Moyenne | Khi deux | Valeur de p |
|---|---|---|---|---|---|
| Somme des carrés des écarts | 32 | 31,60722 | 0,98773 | 31,61 | 0,486 |
| Pearson | 32 | 31,26713 | 0,97710 | 31,27 | 0,503 |
Analyse de la variance
| Test de Wald | |||
|---|---|---|---|
| Source | DL | Khi deux | Valeur de P |
| Régression | 3 | 56,29 | 0,000 |
| Heures depuis nettoyage | 1 | 4,74 | 0,029 |
| Température | 1 | 38,46 | 0,000 |
| Taille de vis | 1 | 13,09 | 0,000 |
Ajustements et diagnostics pour les observations aberrantes
| Observation | Défauts décoloration | Valeur ajustée | Résiduelle | Val. résid. norm. | |
|---|---|---|---|---|---|
| 33 | 43,00 | 58,18 | -2,09 | -2,18 | R |
- Appuyez sur Ctrl+E ou cliquez sur le bouton Modifier la dernière boîte de dialogue
de la barre d'outils Standard. - Cliquez sur Modèle.
- Dans la zone Prédicteurs, sélectionnez Température et Taille de vis.
- En regard de Interactions jusqu’à l’ordre, choisissez 2, puis cliquez sur Ajouter.
- Cliquez sur OK dans chaque boîte de dialogue
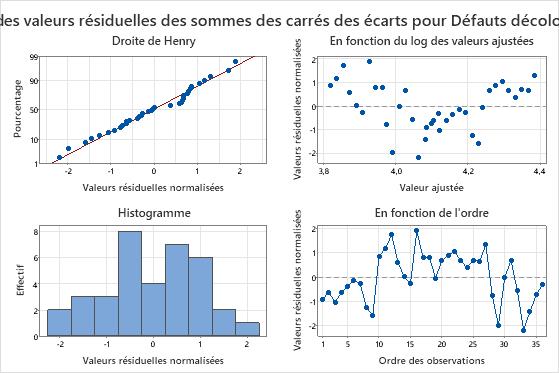
Pour le modèle avec l'interaction, l'AIC est d'environ 236, ce qui est inférieur au modèle sans interaction. L'AIC indique que le modèle avec interaction fonctionne mieux que le modèle sans interaction. La courbure du diagramme des valeurs résiduelles en fonction des valeurs ajustées a disparu. L’ingénieur remarque que certains coefficients ont des valeurs VIF > 5. Dans ce cas, une analyse avec des prédicteurs continus standardisés pour réduire l’effet de la colinéarité donne les mêmes conclusions sur la signification statistique des termes du modèle. (Pour plus d'informations, reportez-vous à la rubrique Multicolinéarité dans la régression.) L'ingénieur décide d'interpréter ce modèle plutôt que celui sans interaction.
Méthode
| Fonction de liaison | Logarithme népérien |
|---|---|
| Codage des prédicteurs de catégorie | (1; 0) |
| Lignes utilisées | 36 |
Equation de régression
| Défauts décoloration | = | exp(Y') |
|---|
| Taille de vis | |||
|---|---|---|---|
| grande | Y' | = | 4,576 + 0,01798 Heures depuis nettoyage - 0,003285 Température |
| petite | Y' | = | 4,032 + 0,01798 Heures depuis nettoyage - 0,000481 Température |
Coefficients
| Terme | Coeff | Coef ErT | Valeur de Z | Valeur de p | FIV |
|---|---|---|---|---|---|
| Constante | 4,5760 | 0,0736 | 62,15 | 0,000 | |
| Heures depuis nettoyage | 0,01798 | 0,00826 | 2,18 | 0,029 | 1,00 |
| Température | -0,003285 | 0,000441 | -7,46 | 0,000 | 1,92 |
| Taille de vis | |||||
| petite | -0,5444 | 0,0990 | -5,50 | 0,000 | 5,37 |
| Température*Taille de vis | |||||
| petite | 0,002804 | 0,000640 | 4,38 | 0,000 | 6,64 |
Récapitulatif du modèle
| R carré de la somme des carrés des écarts | R carré (ajust) de la somme des carrés des écarts | AIC | AICc | BIC |
|---|---|---|---|---|
| 85,99% | 81,46% | 236,05 | 238,05 | 243,97 |
Tests d'adéquation de l'ajustement
| Test | DL | Estimation | Moyenne | Khi deux | Valeur de p |
|---|---|---|---|---|---|
| Somme des carrés des écarts | 31 | 12,36598 | 0,39890 | 12,37 | 0,999 |
| Pearson | 31 | 12,31611 | 0,39729 | 12,32 | 0,999 |
Analyse de la variance
| Test de Wald | |||
|---|---|---|---|
| Source | DL | Khi deux | Valeur de P |
| Régression | 4 | 78,77 | 0,000 |
| Heures depuis nettoyage | 1 | 4,74 | 0,029 |
| Température | 1 | 55,60 | 0,000 |
| Taille de vis | 1 | 30,21 | 0,000 |
| Température*Taille de vis | 1 | 19,17 | 0,000 |
