Sur ce thème
Coefficients
Il existe deux méthodes pour trouver les estimations du maximum de vraisemblance des coefficients. La première consiste à maximiser directement la fonction de vraisemblance relative aux coefficients. Les expressions ne sont pas linéaires dans les coefficients. La méthode alternative consiste à utiliser une approche itérative repé pondérée des moindres carrés (IRWLS), qui est la méthode utilisée par Minitab pour obtenir les estimations des coefficients. McCullagh et Nelder1 montrent que les deux méthodes sont équivalentes. Cependant, la méthode itérative des moindres carrés repondérés est plus facile à appliquer. Pour plus de détails, voir 1.
Méthode d’approximation en une étape pour certains cas de validation croisée k-fold
Pour certains modèles à gros échantillons avec de nombreux plis de validation croisée, Minitab utilise une méthode d’approximation en une étape dans l’algorithme de validation croisée pour diminuer le temps de calcul (voir Pregibon2 et Williams3). Pour ces conceptions, plutôt que d’adapter le modèle de formation pour un pli avec l’algorithme IRWLS à la convergence complète, les statistiques de validation croisée pour le pli proviennent des paramètres de régression de la première étape itérative de l’algorithme.
Le tableau suivant montre quelles conceptions obtiennent des statistiques de validation croisée à partir de l’approximation en 1 étape.
| Effectif d'échantillon (n) | Nombre de colonnes dans la matrice de conception (p) | Nombre de plis (k) |
|---|---|---|
| 200 < n ≤ 500 | 150 < p ≤ 300 | k > 200 |
| p - 300 | k > 100 | |
| 500 < n ≤ 1000 | 100 < p ≤ 300 | k > 300 |
| p - 300 | k > 150 | |
| 1000 < n ≤ 10,000 | p ≤ 50 | k > 1 000 |
| 50 < p ≤ 200 | k > 200 | |
| 200 < p ≤ 400 | k > 50 | |
| p - 400 | k > 10 | |
| 10,000 < n ≤ 50,000 | p ≤ 50 | k > 200 |
| 50 < p ≤ 200 | k > 100 | |
| p - 200 | k > 20 | |
| 50,000 < n ≤ 100,000 | p ≤ 50 | k > 100 |
| 50 < p ≤ 150 | k > 50 | |
| p - 150 | k > 20 | |
| n - 100 000 | Toute valeur de p | k > 100 |
Algorithme d’approximation en une étape
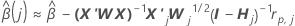
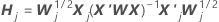
Notation
| Terme | Description |
|---|---|
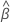 | les coefficients estimés correspondent à l’ensemble complet de données |
| X | la matrice de conception de l’ensemble de données complet |
| X' | la transversale de la matrice de conception pour l’ensemble complet de données |
| W | la matrice de poids pour l’ensemble complet de données |
| X'j | la matrice de conception des données dans le pli jth |
| Wj | la matrice de poids pour les données dans le pli jth |
| Je | matrice d'identité |
| rp, j | le vecteur des résidus Pearson du modèle pour l’ensemble complet de données pour les données dans le pli jth |
[1] P. McCullagh et J. A. Nelder (1989). Modèles linéaires généralisés, 2nd Ed., Chapman & Hall/CRC, Londres.
[2] D. Pregibon (1981). Diagnostics de régression logistique. The Annals of Statistics, 9(4), 705-724.
[3] D. A. Williams (1987). Diagnostics de modèle linéaire généralisés utilisant la déviance et les suppressions de cas uniques, Statistiques appliquées, 36(2), 181-191.
Erreur type des coefficients
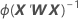
W est une matrice diagonale dans laquelle les éléments diagonaux sont fournis par la formule suivante :
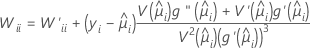
où

La matrice de variance/covariance est fondée sur la matrice hessienne observée au lieu de la matrice d'informations de Fisher. Minitab utilise la matrice hessienne observée, car le modèle obtenu est plus fiable en cas d'erreur de spécification de la moyenne conditionnelle.
Si la liaison canonique est utilisée, la matrice hessienne observée et la matrice d'informations de Fisher sont identiques.
Notation
| Terme | Description |
|---|---|
| yi | valeur de la réponse pour la ie ligne |
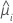 | réponse moyenne estimée pour la ie ligne |
| V(·) | fonction de variance fournie dans le tableau ci-dessous |
| g(·) | fonction de liaison |
| V '(·) | première dérivée de la fonction de variance |
| g'(·) | première dérivée de la fonction de liaison |
| g''(·) | seconde dérivée de la fonction de liaison |
La fonction de variance dépend du modèle :
| Modèle | Fonction de variance |
| Binomiale | 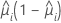 |
| Poisson | 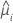 |
Pour plus d'informations, reportez-vous à [1] et à [2].
[1] A. Agresti (1990). Categorical Data Analysis. John Wiley & Sons, Inc.
[2] P. McCullagh et J.A. Nelder (1992). Generalized Linear Model. Chapman & Hall.
Z
La statistique Z sert à déterminer si le prédicteur est associé à la réponse de manière significative. De grandes valeurs absolues de Z indiquent une relation significative. La formule est la suivante :
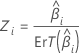
Notation
| Terme | Description |
|---|---|
| Zi | Statistique de test pour une loi normale standard |
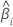 | Coefficient estimé |
 | Erreur type du coefficient estimé |
Pour les petits échantillons, le test du rapport de vraisemblance peut être un test de signification plus fiable. Les valeurs de p du rapport de vraisemblance figurent dans le tableau des sommes des carrés d'écart. Lorsque l'effectif d'échantillon est assez important, les valeurs de p des statistiques Z sont proches des valeurs de p des statistiques du rapport de vraisemblance.
valeur de p (P)
Utilisée dans les tests d'hypothèse pour vous aider à décider de rejeter ou non une hypothèse nulle. La valeur de p est la probabilité d'obtenir une statistique de test au moins aussi extrême que la valeur réelle que vous avez calculée, si l'hypothèse nulle est vérifiée. Une valeur limite couramment utilisée pour la valeur de p est 0,05. Par exemple, si la valeur de p d'une statistique de test est inférieure à 0,05, rejetez l'hypothèse nulle.
Rapports des probabilités de succès pour la régression logistique binaire
Le rapport des probabilités de succès n'est fourni que si vous sélectionnez la fonction de liaison logit pour un modèle avec une réponse binaire. Dans ce cas, le rapport des probabilités de succès sert à interpréter la relation entre un prédicteur et une réponse.
Le rapport des probabilités de succès (τ) peut être tout nombre non négatif. Le rapport des probabilités de succès de 1 sert comme référence de comparaison. Si τ = 1, il n'existe aucune association entre la réponse et le prédicteur. Si τ < 1, les probabilités de succès de l'événement sont supérieures pour le niveau de référence du facteur (ou pour les niveaux inférieurs d'un prédicteur continu). Si τ > 1, les probabilités de succès de l'événement sont inférieures pour le seuil de référence du facteur (ou pour les niveaux inférieurs d'un prédicteur continu). Plus le rapport est éloigné de 1, plus le degré d'association est fort.
Remarque
Pour le modèle de régression logistique binaire avec une covariable ou un facteur, les probabilités de succès estimées sont calculées comme suit :
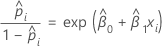
La relation exponentielle fournit une interprétation pour β : les probabilités de succès sont multipliées par eβ1 pour chaque augmentation d'une unité de x. Le rapport des probabilités de succès est équivalent à exp(β1).
Par exemple, si β est égal à 0,75, le rapport des probabilités de succès est de exp(0,75), soit 2,11. Cela indique une augmentation de 111 % des probabilités de succès pour chaque augmentation d'une unité dans x.
Notation
| Terme | Description |
|---|---|
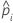 | probabilité estimée de succès pour la ie ligne des données |
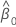 | coefficient estimé de l'ordonnée à l'origine |
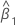 | coefficient estimé pour le prédicteur x |
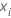 | point de donnée pour la ie ligne |
Intervalle de confiance
L'intervalle de confiance du grand échantillon pour un coefficient estimé est le suivant :
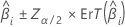
Concernant la régression logistique binaire, Minitab fournit des intervalles de confiance pour les rapports des probabilités de succès. Pour obtenir l'intervalle de confiance des rapports des probabilités de succès, utilisez un exposant pour les limites supérieure et inférieure de l'intervalle de confiance. L'intervalle indique l'étendue des probabilités de succès pour chaque variation d'unité du prédicteur.
Notation
| Terme | Description |
|---|---|
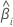 | ie coefficient |
 | probabilité cumulée inverse de la loi normale standard à 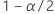 |
 | seuil de signification |
 | erreur type du coefficient estimé |
Matrice de variance/covariance
Matrice d x d, où d représente le nombre de prédicteurs plus un. La variance de chaque coefficient figure dans la cellule en diagonale et la covariance de chaque paire de coefficients figure dans la cellule hors diagonale appropriée. La variance est l'erreur type du carré du coefficient.
La matrice de variance/covariance provient de la dernière itération de la valeur inverse de la matrice d'informations. La matrice de variance/covariance a la forme suivante :
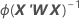
W est une matrice diagonale dans laquelle les éléments diagonaux sont fournis par la formule suivante :

où

La matrice de variance/covariance est fondée sur la matrice hessienne observée au lieu de la matrice d'informations de Fisher. Minitab utilise la matrice hessienne observée, car le modèle obtenu est plus fiable en cas d'erreur de spécification de la moyenne conditionnelle.
Si la liaison canonique est utilisée, la matrice hessienne observée et la matrice d'informations de Fisher sont identiques.
Notation
| Terme | Description |
|---|---|
| yi | valeur de la réponse pour la ie ligne |
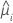 | réponse moyenne estimée pour la ie ligne |
| V(·) | fonction de variance fournie dans le tableau ci-dessous |
| g(·) | fonction de liaison |
| V '(·) | première dérivée de la fonction de variance |
| g'(·) | première dérivée de la fonction de liaison |
| g''(·) | seconde dérivée de la fonction de liaison |
La fonction de variance dépend du modèle :
| Modèle | Fonction de variance |
| Binomiale | 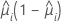 |
| Poisson | 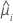 |
Pour plus d'informations, reportez-vous à [1] et à [2].
[1] A. Agresti (1990). Categorical Data Analysis. John Wiley & Sons, Inc.
[2] P. McCullagh et J.A. Nelder (1992). Generalized Linear Model. Chapman & Hall.
