Interprétation des résultats principaux pour la fonction Droite d'ajustement binaire

Suivez les étapes suivantes pour interpréter une droite d'ajustement binaire. Les résultats principaux incluent la valeur de p, la droite d'ajustement, R² de la somme des carrés d'écart et les graphiques des valeurs résiduelles.

Sur ce thème

Etape 1 : Déterminer si l'association entre la réponse et la variable de prédiction est statistiquement significative
Etape 2 : Déterminer les effets des prédicteurs
Etape 3 : Déterminer l'ajustement du modèle à vos données
Etape 4 : Déterminer si votre modèle vérifie les hypothèses de l'analyse

Etape 1 : Déterminer si l'association entre la réponse et la variable de prédiction est statistiquement significative

Pour déterminer si l'association entre la variable de réponse et la variable de prédiction est statistiquement significative, comparez la valeur de p du terme à votre seuil de signification pour évaluer l'hypothèse nulle. L'hypothèse nulle est que le coefficient pour la variable de prédiction est égal à zéro, ce qui indique qu'il n'existe aucune association entre la variable de prédiction et la variable de réponse. En général, un seuil de signification (noté alpha ou α) de 0,05 fonctionne bien. Un seuil de signification de 0,05 indique un risque de 5 % de conclure à tort qu'il existe une association.

Valeur de p ≤ α : l'association est statistiquement significative: Si la valeur de p est inférieure ou égale au seuil de signification, vous pouvez conclure qu'il existe une association statistiquement significative entre la variable de réponse et la variable de prédiction.
Valeur de p > α : l'association n'est pas statistiquement significative: Si la valeur de p est supérieure au seuil de signification, vous ne pouvez pas conclure qu'il existe une association statistiquement significative entre la variable de réponse et la variable de prédiction.

Analyse de la variance

Source	DL	Somme des carrés des écarts ajustée	Moyenne ajustée	Khi deux	Valeur de p
Régression	1	22,7052	22,7052	22,71	0,000
Dose (mg)	1	22,7052	22,7052	22,71	0,000
Erreur	4	0,9373	0,2343
Total	5	23,6425

Résultat principal : valeur de p

Dans ces résultats, la valeur de p de la dose est 0,000, ce qui est inférieur au seuil de signification de 0,05. Ces résultats indiquent que l'association entre la dose et la présence de la bactérie à la fin du traitement est statistiquement significative.

Etape 2 : Déterminer les effets des prédicteurs

Le rapport des probabilités de succès permet de déterminer l'effet d'un prédicteur. Minitab calcule les rapports des probabilités de succès lorsque le modèle utilise la fonction de liaison logit.

Les rapports de probabilités de succès supérieurs à 1 indiquent que l'événement est plus susceptible de se produire à mesure que le prédicteur augmente. Les rapports de probabilités de succès inférieurs à 1 indiquent que l'événement est moins susceptible de se produire à mesure que le prédicteur augmente.

Rapports des probabilités de succès pour les prédicteurs continus

	Incrément	Rapport des probabilités de succès	IC à 95 %
Dose (mg)	0,5	6,1279	(1,7218; 21,8087)

Résultat principal : rapport des probabilités de succès

Dans ces résultats, le modèle utilise le dosage d'un médicament pour prévoir la présence ou l'absence de bactérie chez des sujets adultes. Chaque comprimé contenant une dose de 0,5 mg, les chercheurs utilisent une variation d'unité de 0,5 mg. Le rapport des probabilités de succès est environ de 6. Pour chaque comprimé supplémentaire pris par un adulte, les probabilités de succès concernant le fait qu'un patient n'ait pas la bactérie sont multipliées par 6.

Utilisez la droite d'ajustement pour examiner la relation entre la variable de réponse et la variable de prédiction.

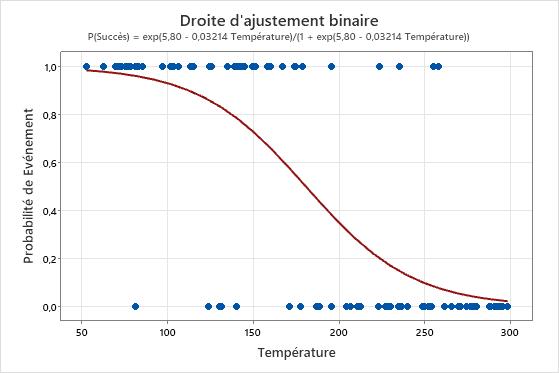
Résultat principal : droite d'ajustement binaire

Dans ces résultats, l'équation est écrite en tant que probabilité de succès. La valeur de réponse 1 sur l'axe des y représente un succès. La droite indique que plus la température augmente, plus la probabilité de succès diminue. Lorsque les températures approchent de 50, la pente de la droite n'est pas très prononcée, ce qui indique que lorsque la température augmente, la probabilité diminue lentement. La droite est plus proche de la verticale au niveau du milieu des données de température, ce qui indique qu'un changement d'un degré dans la température a un effet plus important au niveau de cette étendue. Lorsque la probabilité de succès s'approche de zéro sur l'extrémité supérieure de la plage de températures, la droite s'aplanit à nouveau.

Etape 3 : Déterminer l'ajustement du modèle à vos données

Pour déterminer l'ajustement du modèle aux données, étudiez les statistiques dans le tableau Récapitulatif du modèle. Pour la régression logistique binaire, le format des données affecte les statistiques R² de la somme des carrés d'écart, mais pas l'AIC. Pour plus d'informations, reportez-vous à la rubrique Influence du format des données sur l'ajustement dans la régression logistique binaire.

R carré de la somme des carrés d'écart

Plus le R² de la somme des carrés d'écart est élevé, plus le modèle est ajusté à vos données. Le R² de la somme des carrés d'écart est toujours compris entre 0 et 100 %.

Le R² de la somme des carrés d'écart augmente toujours lorsque vous ajoutez des prédicteurs à un modèle. Par exemple, le meilleur modèle à 5 prédicteurs aura toujours une valeur R² au moins aussi élevée que celle du meilleur modèle à 4 prédicteurs. Par conséquent, le R² de la somme des carrés d'écart est surtout utile pour comparer des modèles de même taille.

Pour la régression logistique binaire, le format des données a un impact sur le R² de la somme des carrés d'écart. Celui-ci est généralement plus élevé pour les données qui sont au format événement/essai. Les R² de la somme des carrés d'écart sont comparables uniquement entre des modèles qui utilisent le même format de données.

La valeur R² de la somme des carrés d'écart n'est qu'une des mesures de l'ajustement du modèle aux données. Même si un modèle a une valeur R² élevée, vous devez consulter les graphiques des valeurs résiduelles pour évaluer l'ajustement du modèle aux données.

R carré (ajust) de la somme des carrés d'écart

Pour comparer des modèles n'ayant pas le même nombre de prédicteurs, utilisez le R² ajusté de la somme des carrés d'écart. Celui-ci augmente toujours lorsque vous ajoutez un prédicteur au modèle. Le R² ajusté de la somme des carrés d'écart intègre le nombre de prédicteurs dans le modèle pour vous aider à choisir le modèle correct.

AIC, AICc et BIC

Pour la fonction Droite d'ajustement binaire, vous pouvez utiliser les critères d'information pour comparer l'ajustement de plusieurs fonctions de liaison ou de différents prédicteurs. Les valeurs faibles sont les valeurs souhaitables. Cela dit, le modèle qui présente les valeurs les plus faibles n'est pas forcément bien ajusté aux données. Vous devez aussi utiliser les diagrammes de test et les graphiques des valeurs résiduelles pour évaluer l'ajustement du modèle aux données.

Récapitulatif du modèle

R carré de la somme des carrés des écarts	R carré (ajust) de la somme des carrés des écarts	AIC	AICc	BIC	Zone située sous la courbe ROC
96,04%	91,81%	10,63	14,63	10,22	0,9398

Résultats principaux : R carré de la somme des carrés d'écart, R carré (ajust) de la somme des carrés d'écart, AIC

Dans ces résultats, le modèle explique 96,04 % de la somme des carrés des écarts dans la variable de réponse. Pour ces données, la valeur R² de la somme des carrés des écarts indique que le modèle fournit un bon ajustement aux données. Si des modèles supplémentaires sont ajustés avec d'autres prédicteurs, utilisez les valeurs de R2 pour comparer l'ajustement des modèles aux données.

Etape 4 : Déterminer si votre modèle vérifie les hypothèses de l'analyse

Les graphiques des valeurs résiduelles permettent de déterminer si le modèle est adapté et si les hypothèses de l'analyse sont vérifiées. Si elles ne le sont pas, il se peut que le modèle ne soit pas ajusté aux données et vous devez être prudent lors de l'interprétation des résultats.

Pour plus d'informations sur la manière de traiter les schémas dans les graphiques des valeurs résiduelles, reportez-vous à la rubrique Graphiques pour la fonction Droite d'ajustement binaire et cliquez sur le nom du graphique des valeurs résiduelles dans la liste située en haut de la page.

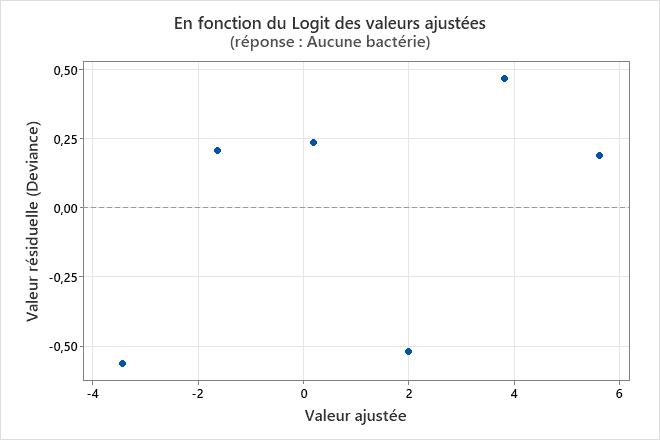
Graphique des valeurs résiduelles en fonction des valeurs ajustées

Utilisez le diagramme des valeurs résiduelles en fonction des valeurs ajustées pour vérifier l'hypothèse selon laquelle les valeurs résiduelles sont normalement distribuées. Dans l'idéal, les points doivent être répartis aléatoirement des deux côtés de 0, sans schéma reconnaissable.

Le graphique des valeurs résiduelles en fonction des valeurs ajustées est uniquement disponible lorsque les données sont au format Evénement/Essai.

Les schémas du tableau suivant peuvent indiquer que le modèle n'est pas adapté.

Schéma	Ce que le schéma indique
Eparpillement ou répartition déséquilibrée des valeurs résiduelles en fonction des valeurs ajustées	Une fonction de liaison inadaptée
Curviligne	Un terme d'ordre supérieur manquant ou une fonction de liaison inadaptée
Un point très éloigné de zéro	Une valeur aberrante
Un point éloigné des autres points dans le sens des x	Un point influent

Dans ce graphique des valeurs résiduelles en fonction des valeurs ajustées, les données semblent être distribuées aléatoirement autour de zéro. Rien ne permet de penser que les valeurs résiduelles dépendent des valeurs ajustées.

Graphique des valeurs résiduelles en fonction de l'ordre

Utilisez le diagramme des valeurs résiduelles en fonction de l'ordre pour vérifier l'hypothèse selon laquelle les valeurs résiduelles sont indépendantes les unes par rapport aux autres. Les valeurs résiduelles indépendantes ne présentent aucune tendance ou schéma lorsqu'elles sont affichées dans un ordre chronologique. La présence de schémas dans les points peut indiquer que les valeurs résiduelles qui sont proches les unes des autres peuvent être corrélées, et ne sont donc pas indépendantes. Idéalement, les valeurs résiduelles du graphique doivent être réparties de façon aléatoire autour de la ligne centrale.

Si vous observez un schéma, étudiez-en la cause. Les types de schémas suivants peuvent indiquer que les valeurs résiduelles sont corrélées.

Dans ce graphique des valeurs résiduelles en fonction de l'ordre, les valeurs résiduelles semblent être réparties de façon aléatoire autour de la ligne centrale. Rien ne permet de penser que les valeurs résiduelles ne sont pas indépendantes.