Sur ce thème
Droite d'ajustement binaire
La droite d'ajustement affiche les données de prévision et de réponse. Le graphique comprend la droite de régression, qui représente l'équation de régression. Vous pouvez également afficher l'intervalle de confiance pour les valeurs ajustées.
Interprétation
Utilisez la droite d'ajustement pour examiner la relation entre la variable de réponse et la variable de prédiction.
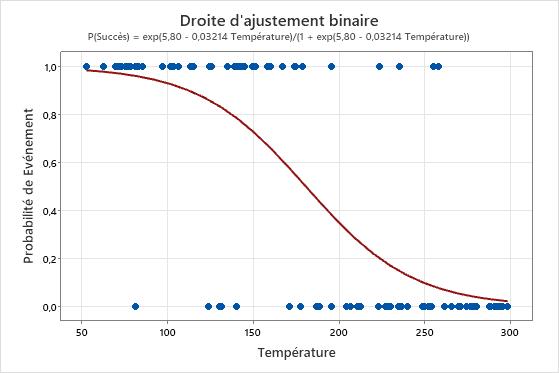
Dans ces résultats, l'équation est écrite en tant que probabilité de succès. La valeur de réponse 1 sur l'axe des y représente un succès. La droite indique que plus la température augmente, plus la probabilité de succès diminue. Lorsque les températures approchent de 50, la pente de la droite n'est pas très prononcée, ce qui indique que lorsque la température augmente, la probabilité diminue lentement. La droite est plus proche de la verticale au niveau du milieu des données de température, ce qui indique qu'un changement d'un degré dans la température a un effet plus important au niveau de cette étendue. Lorsque la probabilité de succès s'approche de zéro sur l'extrémité supérieure de la plage de températures, la droite s'aplanit à nouveau.
Si le modèle est correctement ajusté aux données, les probabilités prévues élevées indiquent les valeurs pour lesquelles l'événement est courant. Lorsque les températures approchent de 50, la valeur de réponse 1 est la plus courante. Plus la température augmente, plus la valeur de réponse zéro est courante.
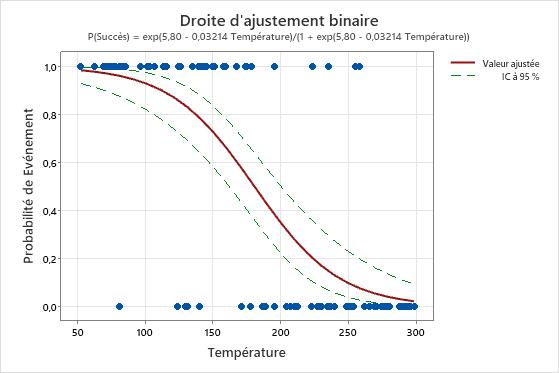
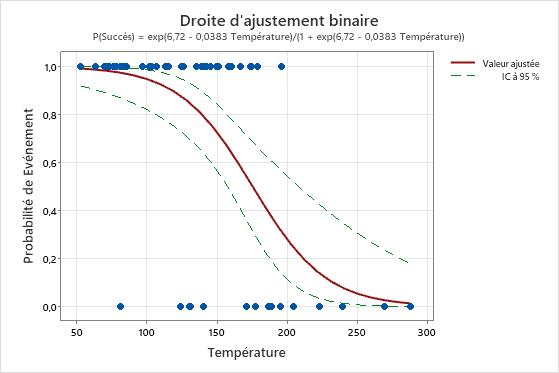
Si vous ajoutez des intervalles de confiance au graphique, vous pouvez les utiliser pour évaluer la précision des estimations des valeurs ajustées. Dans le premier graphique ci-dessous, les segments représentant l'intervalle de confiance restent à peu près de la même longueur à mesure que le prédicteur augmente. Dans le deuxième graphique, l'intervalle de confiance s'élargit à mesure que la valeur du prédicteur augmente. La largeur du plus grand intervalle est partiellement due à la petite quantité de données lorsque la température est élevée.
Histogramme des valeurs résiduelles
L'histogramme des valeurs résiduelles des sommes des carrés d'écart montre la distribution des valeurs résiduelles pour toutes les observations.
Interprétation
| Schéma | Ce que le schéma indique |
|---|---|
| Longue extrémité dans une direction | Asymétrie |
| Barre éloignée des autres | Une valeur aberrante |
Comme l'apparence de l'histogramme dépend du nombre d'intervalles utilisés pour regrouper les données, n'évaluez pas la normalité des valeurs résiduelles à l'aide d'un histogramme. Utilisez plutôt une droite de Henry.
Droite de Henry des valeurs résiduelles
La droite de Henry des valeurs résiduelles affiche les valeurs résiduelles en fonction de leurs valeurs attendues lorsque la loi de distribution est normale.
Interprétation
Utilisez la droite de Henry des valeurs résiduelles afin de vérifier l'hypothèse selon laquelle les valeurs résiduelles sont normalement distribuées. La droite de Henry des valeurs résiduelles doit suivre approximativement une ligne droite.
Une courbe S implique une distribution aux extrémités allongées.
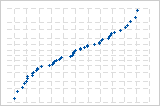
Une courbe S inversée implique une distribution aux extrémités écourtées.

Une courbe descendante implique une loi asymétrique à droite.

Quelques points situés loin de la ligne impliquent une distribution comportant des valeurs aberrantes.
Si vous observez une tendance non normale, utilisez les autres graphiques des valeurs résiduelles pour rechercher tout autre problème éventuel avec le modèle, tel que des termes manquants ou l'effet d'un ordre temporel. Si les valeurs résiduelles ne suivent pas une loi normale, les intervalles de confiance pour l'approximation selon la loi normale et les valeurs de p du test Wald peuvent être inexacts.
Valeurs résiduelles en fonction des valeurs ajustées
Le diagramme des valeurs résiduelles en fonction des valeurs ajustées affiche les valeurs résiduelles sur l'axe des y et les valeurs ajustées sur l'axe des x. Le graphique est utile lorsque les données sont au format événement/essai. Lorsque les données sont au format réponse binaire/effectif, Minitab ne le fournit pas.
Interprétation
Utilisez le diagramme des valeurs résiduelles en fonction des valeurs ajustées pour vérifier l'hypothèse selon laquelle les valeurs résiduelles sont normalement distribuées. Dans l'idéal, les points doivent être répartis aléatoirement des deux côtés de 0, sans schéma reconnaissable.
| Schéma | Ce que le schéma indique |
|---|---|
| Eparpillement ou répartition déséquilibrée des valeurs résiduelles en fonction des valeurs ajustées | Une fonction de liaison inadaptée |
| Curviligne | Un terme d'ordre supérieur manquant ou une fonction de liaison inadaptée |
| Un point très éloigné de zéro | Une valeur aberrante |
| Un point éloigné des autres points dans le sens des x | Un point influent |

Graphique avec valeur aberrante
Un des points a une valeur beaucoup élevée que tous les autres. Il s'agit donc d'une valeur aberrante. S'il existe un trop grand nombre de valeurs aberrantes, le modèle n'est peut-être pas acceptable. Vous devez essayer de déterminer la cause de toutes les valeurs aberrantes. Corrigez les erreurs de mesure ou d’entrée des données. Pensez éventuellement à supprimer les valeurs de données associées à des événements anormaux et uniques (causes spéciales). Ensuite, répétez l'analyse.
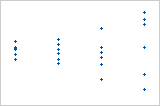
Graphique avec variance non constante
La variance des valeurs résiduelles augmente avec les valeurs ajustées. Plus les valeurs ajustées augmentent, plus les valeurs résiduelles sont dispersées. Ce schéma indique que les variances des valeurs résiduelles sont inégales (non constantes).
| Problème | Solution possible |
|---|---|
| Variance non constante | Envisagez d'utiliser d'autres termes dans le modèle, une autre fonction de liaison ou des pondérations |
| Une valeur aberrante ou un point influant |
|
Valeurs résiduelles en fonction de l'ordre
Le diagramme des valeurs résiduelles en fonction de l'ordre affiche les valeurs résiduelles dans l'ordre dans lequel les données ont été collectées.
Interprétation
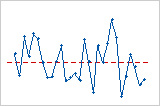
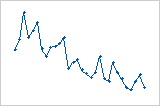
Tendance
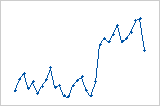
Equipe
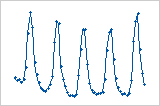
Cycle
Valeurs résiduelles en fonction des variables
Le diagramme des valeurs résiduelles en fonction des variables affiche les valeurs résiduelles en fonction d'une autre variable. La variable peut déjà être présente dans votre modèle. Il se peut aussi que la variable ne soit pas dans le modèle, mais que vous la soupçonniez d'avoir un effet sur la réponse.
Interprétation
Si vous observez un schéma non aléatoire dans les valeurs résiduelles, cela signifie que la variable influe sur la réponse de manière systématique. Vous devez sans doute inclure cette variable dans une analyse.
