Un chercheur médical souhaite déterminer dans quelle mesure la posologie d'un nouveau médicament agit sur la présence de bactéries chez l'adulte. Le chercheur conduit une expérience avec 30 patients et 6 niveaux posologiques. Pendant deux semaines, il administre une dose donnée à 5 patients, une autre à 5 autres patients, et ainsi de suite. A la fin de la période de deux semaines, chaque patient est testé pour déterminer la présence éventuelle de bactéries.
Les données incluant une réponse binaire et un prédicteur continu, le chercheur utilise une droite d'ajustement binaire pour déterminer s'il existe une relation entre la posologie du médicament et la présence de bactéries.
- Ouvrez le fichier de données échantillons, MédicamentBactéries.MTW.
- Sélectionnez .
- Dans la liste déroulante, sélectionnez Réponse au format : événement/essai.
- Dans la zone Nom d'événement, tapez Aucune bactérie.
- Dans la zone Nombre d'événements, saisissez "Aucune bactérie".
- Dans la zone Nombre d'essais, saisissez Essais.
- Dans la zone Prédicteur, saisissez "Dose (mg)".
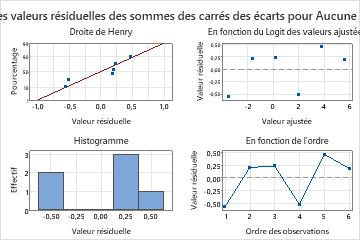
- Cliquez sur Graphiques. Sous Graphiques des valeurs résiduelles, sélectionnez Quatre en un.
- Cliquez sur OK dans chaque boîte de dialogue.
Interprétation des résultats
La valeur de p pour le dosage médical est inférieure au seuil de signification de 0,05. Ces résultats indiquent que la relation entre le dosage du médicament et la présence de la bactérie est statistiquement significative. La droite d'ajustement binaire montre que lorsque le dosage augmente, la probabilité de n'avoir aucune bactérie augmente. De plus, le rapport des probabilités de succès indique que pour chaque augmentation du dosage de 1 mg, la probabilité qu'aucune bactérie ne soit présente augmente d'environ 38 fois. La droite d'ajustement indique que le modèle est bien ajusté aux données et les graphiques des valeurs résiduelles n'indiquent aucun problème pour ce modèle.
Méthode
| Fonction de liaison | Logit |
|---|---|
| Lignes utilisées | 6 |
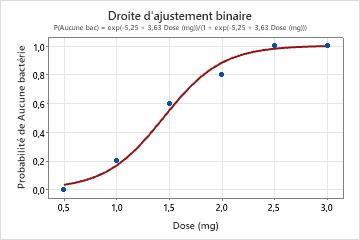
Informations de réponse
| Variable | Valeur | Dénombrement | Nom d'événement |
|---|---|---|---|
| Aucune bactérie | Evénement | 18 | Aucune bactérie |
| Non-événement | 12 | ||
| Essais | Total | 30 |
Equation de régression
| P(Aucune bactérie) = exp(-5,25 + 3,63 Dose (mg))/(1 + exp(-5,25 + 3,63 Dose (mg))) |
|---|
Coefficients
| Terme | Coeff | Coef ErT | FIV |
|---|---|---|---|
| Constante | -5,25 | 1,99 | |
| Dose (mg) | 3,63 | 1,30 | 1,00 |
Rapports des probabilités de succès pour les prédicteurs continus
| Rapport des probabilités de succès | IC à 95 % | |
|---|---|---|
| Dose (mg) | 37,5511 | (2,9647; 475,6190) |
Récapitulatif du modèle
| R carré de la somme des carrés des écarts | R carré (ajust) de la somme des carrés des écarts | AIC | AICc | BIC |
|---|---|---|---|---|
| 96,04% | 91,81% | 10,63 | 14,63 | 10,22 |
Analyse de la variance
| Source | DL | Somme des carrés des écarts ajustée | Moyenne ajustée | Khi deux | Valeur de p |
|---|---|---|---|---|---|
| Régression | 1 | 22,7052 | 22,7052 | 22,71 | 0,000 |
| Dose (mg) | 1 | 22,7052 | 22,7052 | 22,71 | 0,000 |
| Erreur | 4 | 0,9373 | 0,2343 | ||
| Total | 5 | 23,6425 |
