Sur ce thème
Méthode de calcul
Pour la régression sur les meilleurs sous-ensembles, Minitab utilise une procédure appelée chemin hamiltonien, qui est une méthode permettant de calculer tous les sous-ensembles de prédicteurs possibles, à raison d'un sous-ensemble par étape. Plus précisément, Minitab calcule l'intégralité des 2**m - 1 sous-ensembles en 2**m - 1 étapes, où m est le nombre de prédicteurs dans le modèle. A chaque étape, Minitab évalue la régression sur un sous-ensemble.
Chaque sous-ensemble du chemin hamiltonien diffère du précédent par l'ajout ou la suppression d'une seule variable. A chaque étape du chemin hamiltonien, l'opérateur de balayage ajoute une variable à la régression ou en retire une, puis calcule le R2 de chaque sous-ensemble.
Equation de régression
Pour un modèle avec plusieurs prédicteurs, l'équation est la suivante :
y = β0 + β1x1 + … + βkxk + ε
L'équation ajustée est la suivante :
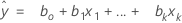
Dans la régression linéaire simple, qui comprend un seul prédicteur, le modèle est le suivant :
y=ß0+ ß1x1+ε
A l'aide des estimations de régression b0 pour ß0 et b1 pour ß1, l'équation ajustée est la suivante :
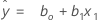
Notation
| Terme | Description |
|---|---|
| y | variable |
| xk | ke terme. Chaque terme peut être un prédicteur unique, un terme polynomial ou un terme d'interaction. |
| ßk | ke coefficient de régression de la population |
| ε | terme d'erreur qui suit une loi normale avec une moyenne de 0 |
| bk | estimation du ke coefficient de régression de la population |
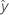 | réponse ajustée |
R carré
Le R2 est également appelé coefficient de détermination.
Formule

Notation
| Terme | Description |
|---|---|
| yi | ie valeur de réponse observée |
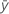 | réponse moyenne |
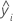 | ie réponse ajustée |
R carré (ajust)

Notation
| Terme | Description |
|---|---|
| CM | Carré moyen |
| SC | Somme des carrés |
| DL | Degrés de liberté |
PRESS
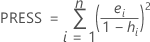
Notation
| Terme | Description |
|---|---|
| n | nombre d'observations |
| ei | ie valeur résiduelle |
| hi | ie élément diagonal de X (X' X)-1X' |
R carré (prév)

Minitab affiche zéro lorsque les calculs de R2 (prév) génèrent des valeurs négatives.
Notation
| Terme | Description |
|---|---|
| yi | ie valeur de réponse observée |
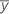 | réponse moyenne |
| n | nombre d'observations |
| ei | ie valeur résiduelle |
| hi | ie élément sur la diagonale de X(X'X)–1X' |
| X | matrice du plan |
Cp de Mallows
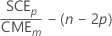
Notation
| Terme | Description |
|---|---|
| SCEp | somme des carrés de l'erreur pour le modèle examiné |
| CMEm | carré moyen de l'erreur pour le modèle incluant tous les termes candidats |
| n | nombre d'observations |
| p | nombre de termes dans le modèle, constante incluse |
S

Notation
| Terme | Description |
|---|---|
| CA MOY ERR | carré moyen de l'erreur |
Log de vraisemblance


Les observations dont la pondération est de 0 ne sont pas dans l'analyse.
Notation
| Terme | Description |
|---|---|
| n | nombre d'observations |
| R | somme des carrés de l'erreur pour le modèle |
| wi | pondération pour l'ie observation |
AICc (critère d'information d'Akaike corrigé)
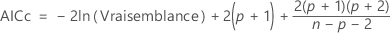
La valeur AICc n'est pas calculée quand  .
.
Notation
| Terme | Description |
|---|---|
| n | nombre d'observations |
| p | nombre de coefficients dans le modèle, constante incluse |
BIC (critère d'information bayésien)

Notation
| Terme | Description |
|---|---|
| p | nombre de coefficients dans le modèle, constante incluse |
| n | nombre d'observations |
Conditionnement

Notation
| Terme | Description |
|---|---|
| C | conditionnement |
| λmaximum | valeur propre maximale issue de la matrice de corrélation des termes du modèle, sans inclure la valeur à l'origine |
| λminimum | valeur propre minimale issue de la matrice de corrélation des termes du modèle, sans inclure la valeur à l'origine |
