Remarque
Cette commande est disponible avec le Module d'analyse prédictive. Cliquez ici pour plus d'informations sur l'activation du module.
Les modèles TreeNet® sont une approche de la résolution de problèmes de classification et de régression à la fois plus exacts et plus résistants au surajustement qu'un seul arbre de classification ou de régression. De manière générale, ce procédé consiste à commencer par un modèle initial composé d'un petit arbre de régression. Cet arbre donne des valeurs résiduelles pour chaque ligne des données qui deviennent la variable de réponse pour l’arbre de régression suivant. Nous construisons un autre petit arbre de régression pour prédire les valeurs résiduelles à partir du premier arbre et calculons à nouveau les valeurs résiduelles résultantes. Nous répétons cette séquence jusqu'à ce qu'un nombre optimal d'arbres présentant une erreur de prédiction minimale soit identifié à l'aide d'une méthode de validation. La séquence d'arbres qui en résulte constitue le modèle de régression TreeNet®.
Pour le cas de régression, nous pouvons ajouter une description générale de l’analyse, mais certains détails dépendent de la fonction de perte choisie parmi les suivantes :
| Statistique | Valeur |
|---|---|
Ajustement initial,  |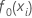
moyenne de la variable de réponse |
Valeur résiduelle généralisée, 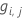 comme valeur de réponse pour la ligne i |
 |
Dans les mises à jour des nœuds,  |
moyenne de  |
| Statistique | Valeur |
|---|---|
Ajustement initial,  |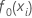
médiane de la variable de réponse |
Valeur résiduelle généralisée, 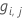 comme valeur de réponse pour la ligne i |
 |
Dans les mises à jour des nœuds,  |
médiane de  |
Fonction perte Huber
Pour la fonction de perte Huber, les statistiques sont les suivantes :
L’ajustement initial,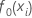 
, est égal à la médiane de toutes les valeurs de réponse.
Pour le développement du je arbre, 
La valeur résiduelle généralisée pour la ie ligne est alors la suivante :
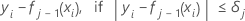
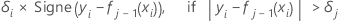
Les valeurs résiduelles généralisées sont utilisés comme valeurs de réponse pour développer le je arbre.
La valeur mise à jour pour les lignes dans le me nœud terminal du le arbre est la suivante :
comme valeur résiduelle standard pour la ie ligne après le développement de j-1 arbres. Soit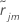 
Comme la médiane des 
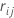valeurs pour les lignes à l’intérieur du nœud terminal m du je arbre. Ensuite, la valeur mise à jour pour chaque ligne à l’intérieur du me nœud terminal du je arbre est :
La moyenne dans l’expression précédente est calculée sur toutes les lignes à l’intérieur du nœud terminal m du le arbre.
Notation pour les fonctions de perte
Dans les détails précédents,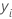 
est la valeur de la variable de réponse pour la ligne i,
est la valeur ajustée des j – 1 arbres précédents, et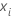 
est un vecteur qui représente la ie ligne des valeurs du prédicteur dans les données d'apprentissage.
Paramètres d’entrée
| Entrée | Symbole |
|---|---|
| taux d'apprentissage |  |
| taux d'échantillonnage |  |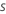
| nombre maximal de nœuds terminaux par arbre |  |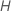
| nombre d'arbres |  |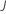
| valeur de conversion |  |
Processus général
- Tirez un échantillon aléatoire de taille s * N à partir des données d'apprentissage, où N est le nombre de lignes dans ces données.
- Calculez les valeurs résiduelles généralisées,
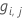, pour 
. - Ajustez un arbre de régression avec au maximum M nœuds terminaux aux valeurs résiduelles généralisées. L'arbre divise les observations en groupes M maximaux qui s'excluent mutuellement.
- Pour le me nœud terminal dans l'arbre de régression, calculez les mises à jour internes au nœud pour l'arbre qui dépendent de la fonction de perte,
. - Réduisez les mise à jour à l'intérieur du nœud du taux d'apprentissage et appliquez les valeurs pour les valeurs ajustées mises à jour,
:
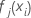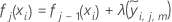
- Répétez les étapes 1 à 5 pour les J arbres de l'analyse.
