Remarque
Cette commande est disponible avec la commande Module d'analyse prédictive. Cliquez ici pour plus d’informations sur la façon d’activer le module.
Une équipe de chercheurs souhaite utiliser les données d’un processus de moulage par injection pour étudier les paramètres des machines qui maximisent un type de résistance d’une pièce en plastique. Les variables comprennent les commandes sur les machines, les différentes formules de plastique et les machines de moulage par injection.
Dans le cadre de l’exploration initiale des données, l’équipe décide Découvrir les prédicteurs principaux de comparer les modèles en supprimant séquentiellement les prédicteurs sans importance afin d’identifier les prédicteurs clés. Les chercheurs espèrent identifier les principaux prédicteurs qui ont le plus d’effet sur la réponse et mieux comprendre les relations entre la réponse et les principaux prédicteurs.
- Ouvrez l’exemple de jeu de données processus_d’injection.MWX.
- Choisissez .
- Dans Réponse, entrez force.
- Dans Prédicteurs continus, entrez 'pression d’injection' – 'température à mesure'.
- Dans Prédicteurs de catégorie, entrez machine et formule.
- Cliquez sur OK.
Interpréter les résultats
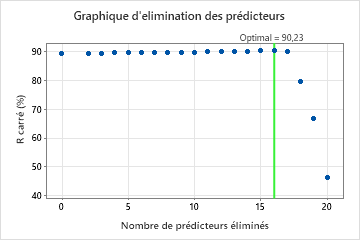
Pour cette analyse, Minitab Statistical Software compare 20 modèles. L’astérisque dans la colonne Modèle de la table d’évaluation du modèle indique que le modèle avec la valeur la plus élevée de la statistique R2 à validation croisée est le modèle 16. Le modèle 16 contient 5 prédicteurs importants. Les résultats qui suivent le tableau d’évaluation du modèle concernent le modèle 16.
Bien que le modèle 16 ait la plus grande valeur de la statistique R2 à validation croisée, d’autres modèles ont des valeurs similaires. L’équipe peut cliquer Sélectionner un autre modèle pour produire des résultats pour d’autres modèles à partir du tableau d’évaluation du modèle.
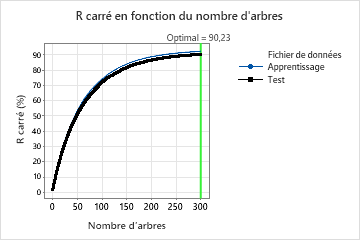
Dans les résultats du modèle 16, le graphique R au carré en fonction du nombre d’arbres montre que le nombre optimal d’arbres est égal au nombre d’arbres dans l’analyse, 300. L’équipe peut cliquer Régler les hyperparamètres pour augmenter le nombre d’arbres et voir si les modifications apportées à d’autres hyperparamètres améliorent les performances du modèle.
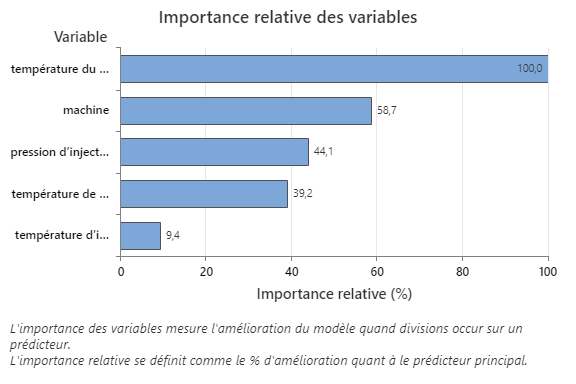
Le graphique Importance relative des variables trace les prédicteurs dans l’ordre de leur effet sur l’amélioration du modèle lorsque des divisions sont effectuées sur un prédicteur au cours de la séquence d’arbres. La variable prédictive la plus importante est la température du moule. Si l’importance de la variable prédictive principale, la température du moule, est de 100 %, la variable importante suivante, Machine, a une contribution de 58,7 %. Cela signifie que la machine qui injecte est 58,7% aussi importante que la température à l’intérieur du moule.
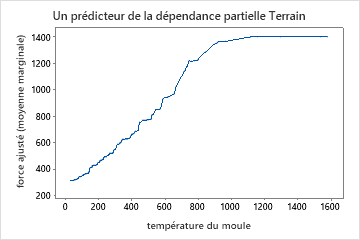
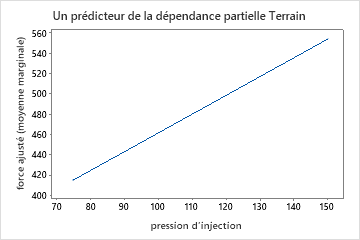
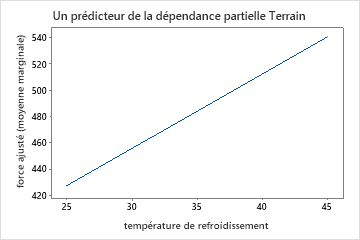
Utilisez les diagrammes de dépendance partielle pour obtenir des informations sur la façon dont les variables importantes ou les paires de variables affectent la réponse prédite. Les graphiques de dépendance partielle montrent si la relation entre la réponse et une variable est linéaire, monotone ou plus complexe.
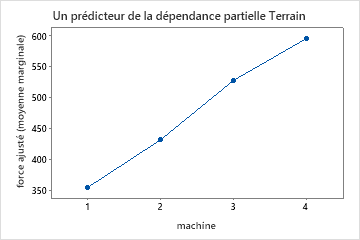
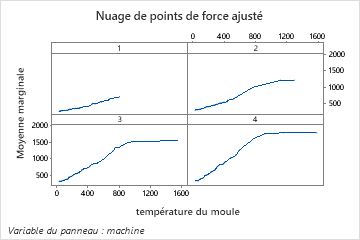
Les graphiques de dépendance partielle à un prédicteur montrent que la température du moule, la pression d’injection et la température de refroidissement ont toutes une relation positive avec la résistance. Le graphique des machines montre les différences entre les machines, la machine 1 fabriquant les pièces les plus faibles en moyenne et la machine 4 fabriquant les pièces les plus solides en moyenne. L’équipe remarque que la température du moule et la machine ont l’interaction la plus forte dans les données, ils examinent donc le graphique de dépendance partielle à deux prédicteurs pour mieux comprendre comment ces variables affectent la résistance. L’équipe peut sélectionner dans les résultats de produire des graphiques pour d’autres variables, telles que la température d’injection.
Le graphique de dépendance partielle à deux prédicteurs de la température du moule et de la machine donne un aperçu de la différence de résistance moyenne des machines. L’une des raisons est que les données de la machine 1 ne comprennent pas autant d’observations aux températures de moule les plus élevées que les autres machines. L’équipe pourrait toujours décider de chercher d’autres raisons pour lesquelles les machines produisent des forces différentes lorsque d’autres paramètres sont les mêmes. L’équipe peut cliquer sur les résultats pour produire des graphiques pour d’autres paires de variables.
Méthode
| Fonction de perte | Erreur quadratique |
|---|---|
| Critères de sélection du nombre d'arbres optimal | R carré maximum |
| Validation de modèle | Validation croisée pour 3 ensemble(s) |
| Taux d'apprentissage | 0,01408 |
| Fraction de sous-échantillon | 0,5 |
| Nombre maximal de nœuds terminaux par arbre | 6 |
| Taille minimale du nœud terminal | 3 |
| Nombre de prédicteurs sélectionnés pour la partition des nœuds | Nombre total de prédicteurs = 21 |
| Lignes utilisées | 1408 |
Informations de réponse
| Moyenne | EcTyp | Minimum | Q1 | Médiane | Q3 | Maximum |
|---|---|---|---|---|---|---|
| 485,247 | 318,611 | 41,2082 | 301,099 | 398,924 | 562,449 | 2569,04 |
Sélection du modèle en éliminant les prédicteurs non importants
| Modèle | Nombre optimal d'arbres | R carré (%) | Nombre de prédicteurs | Prédicteurs éliminés |
|---|---|---|---|---|
| 1 | 300 | 89,32 | 21 | Aucun |
| 2 | 300 | 89,34 | 19 | débit en plastique; changer de position |
| 3 | 300 | 89,39 | 18 | température de séchage |
| 4 | 300 | 89,46 | 17 | zone de température de fonte 2 |
| 5 | 300 | 89,51 | 16 | température plastique |
| 6 | 300 | 89,50 | 15 | formule |
| 7 | 300 | 89,59 | 14 | maintenir la pression |
| 8 | 300 | 89,57 | 13 | coussin à vis |
| 9 | 300 | 89,69 | 12 | zone de température de fonte 4 |
| 10 | 300 | 89,70 | 11 | pression arrière |
| 11 | 300 | 89,86 | 10 | zone de température de fonte 1 |
| 12 | 300 | 89,90 | 9 | temps de séchage |
| 13 | 300 | 89,92 | 8 | température à mesure |
| 14 | 300 | 90,06 | 7 | zone de température de fonte 5 |
| 15 | 300 | 90,16 | 6 | zone de température de fonte 3 |
| 16* | 300 | 90,23 | 5 | vitesse de rotation de vis |
| 17 | 300 | 89,96 | 4 | température d’injection |
| 18 | 297 | 79,37 | 3 | température de refroidissement |
| 19 | 244 | 66,64 | 2 | pression d’injection |
| 20 | 164 | 46,19 | 1 | machine |
Récapitulatif du modèle
| Nombre total de prédicteurs | 5 |
|---|---|
| Prédicteurs importants | 5 |
| Nombre d'arbres développés | 300 |
| Nombre optimal d'arbres | 300 |
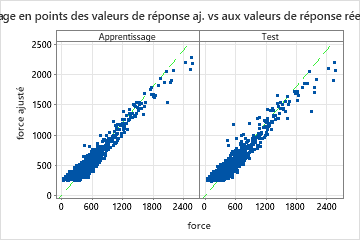
| Statistiques | Apprentissage | Test |
|---|---|---|
| R carré | 92,23% | 90,23% |
| Racine de l'erreur quadratique moyenne (RMSE) | 88,8049 | 99,5673 |
| Erreur quadratique moyenne (MSE) | 7886,3152 | 9913,6420 |
| Ecart absolu moyen (MAD) | 68,9231 | 74,4113 |
| Pourcentage d'erreur absolue moyen (MAPE) | 0,2083 | 0,2175 |