Remarque
Cette commande est disponible avec la commande Module d'analyse prédictive. Cliquez ici pour plus d’informations sur la façon d’activer le module.
Une équipe de chercheurs veut utiliser des données sur un emprunteur et l’emplacement d’une propriété pour prédire le montant d’un prêt hypothécaire. Les variables comprennent le revenu, la race et le sexe de l’emprunteur ainsi que l’emplacement de la propriété dans le secteur de recensement et d’autres informations sur l’emprunteur et le type de propriété.
Après une première exploration pour Régression CART® identifier les prédicteurs importants, l’équipe considère Régression TreeNet® maintenant comme une étape de suivi nécessaire. Les chercheurs espèrent mieux comprendre les relations entre la réponse et les prédicteurs importants et prédire de nouvelles observations avec une plus grande précision.
Ces données ont été adaptées sur la base d’un ensemble de données publiques contenant des informations sur les prêts hypothécaires des banques fédérales de prêts immobiliers. Les données originales proviennent de fhfa.gov.
- Ouvrez l’exemple de jeu de données EmpruntsContractés.MTW.
- Choisissez .
- Dans Réponse, entrez Montant du prêt.
- Dans Prédicteurs continus, entrez Revenu annuel – Revenu du secteur.
- Dans Prédicteurs de catégorie, entrez Primo-accédant à la propriété – Zone statistique de base.
- Cliquez sur Validation.
- Dans Méthode de validation, sélectionnez Validation croisée sur K ensembles.
- Dans Nombre de partitions (K), entrez 3.
- Cliquez dans OK chaque boîte de dialogue.
Interpréter les résultats
Pour cette analyse, Minitab cultive 300 arbres et le nombre optimal d’arbres est de 300. Étant donné que le nombre optimal d’arbres est proche du nombre maximal d’arbres que le modèle cultive, les chercheurs répètent l’analyse avec plus d’arbres.
Récapitulatif du modèle
| Nombre total de prédicteurs | 34 |
|---|---|
| Prédicteurs importants | 19 |
| Nombre d'arbres développés | 300 |
| Nombre optimal d'arbres | 300 |
| Statistiques | Apprentissage | Test |
|---|---|---|
| R carré | 94,02% | 84,97% |
| Racine de l'erreur quadratique moyenne (RMSE) | 32334,5587 | 51227,9431 |
| Erreur quadratique moyenne (MSE) | 1,04552E+09 | 2,62430E+09 |
| Ecart absolu moyen (MAD) | 22740,1020 | 35974,9695 |
| Pourcentage d'erreur absolue moyen (MAPE) | 0,1238 | 0,1969 |
Exemple avec 500 arbres
- Sélectionnez Régler les hyperparamètres dans les résultats.
- Dans Nombre d'arbres, entrez 500.
- Cliquez sur Afficher les résultats.
Interpréter les résultats
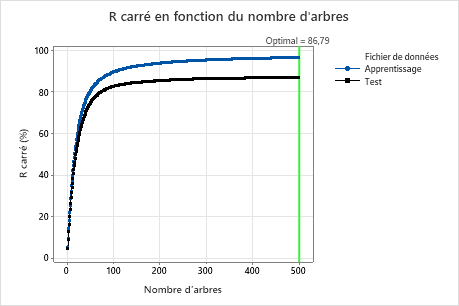
Pour cette analyse, il y avait 500 arbres cultivés et le nombre optimal d’arbres pour la combinaison des hyperparamètres avec la meilleure valeur du critère de précision est de 500. La fraction du sous-échantillon passe à 0,7 au lieu de 0,5 dans l’analyse initiale. Le taux d’apprentissage passe à 0,0437 au lieu de 0,04372 dans l’analyse initiale.
Examinez à la fois le tableau récapitulatif du modèle et le graphique R au carré en fonction du nombre d’arbres. La valeur R2 lorsque le nombre d’arbres est de 500 est de 86,79 % pour les données de test et de 96,41 % pour les données d’entraînement. Ces résultats montrent une amélioration par rapport à une analyse de régression traditionnelle et à un Régression CART®.
Méthode
| Fonction de perte | Erreur quadratique |
|---|---|
| Critères de sélection du nombre d'arbres optimal | R carré maximum |
| Validation de modèle | Validation croisée pour 3 ensemble(s) |
| Taux d'apprentissage | 0,04372 |
| Fraction de sous-échantillon | 0,5 |
| Nombre maximal de nœuds terminaux par arbre | 6 |
| Taille minimale du nœud terminal | 3 |
| Nombre de prédicteurs sélectionnés pour la partition des nœuds | Nombre total de prédicteurs = 34 |
| Lignes utilisées | 4372 |
Informations de réponse
| Moyenne | EcTyp | Minimum | Q1 | Médiane | Q3 | Maximum |
|---|---|---|---|---|---|---|
| 235217 | 132193 | 23800 | 136000 | 208293 | 300716 | 1190000 |
Méthode
| Fonction de perte | Erreur quadratique |
|---|---|
| Critères de sélection du nombre d'arbres optimal | R carré maximum |
| Validation de modèle | Validation croisée pour 3 ensemble(s) |
| Taux d'apprentissage | 0,001; 0,0437; 0,1 |
| Fraction de sous-échantillon | 0,5; 0,7 |
| Nombre maximal de nœuds terminaux par arbre | 6 |
| Taille minimale du nœud terminal | 3 |
| Nombre de prédicteurs sélectionnés pour la partition des nœuds | Nombre total de prédicteurs = 34 |
| Lignes utilisées | 4372 |
Informations de réponse
| Moyenne | EcTyp | Minimum | Q1 | Médiane | Q3 | Maximum |
|---|---|---|---|---|---|---|
| 235217 | 132193 | 23800 | 136000 | 208293 | 300716 | 1190000 |
Optimisation des hyperparamètres
| Modèle | Nombre optimal d'arbres | R carré (%) | Écart absolu moyen | Taux d'apprentissage | Fraction de sous-échantillon | Nombre maximal de nœuds terminaux |
|---|---|---|---|---|---|---|
| 1 | 500 | 36,43 | 82617,1 | 0,0010 | 0,5 | 6 |
| 2 | 495 | 85,87 | 34560,5 | 0,0437 | 0,5 | 6 |
| 3 | 495 | 85,63 | 34889,3 | 0,1000 | 0,5 | 6 |
| 4 | 500 | 36,86 | 82145,0 | 0,0010 | 0,7 | 6 |
| 5* | 500 | 86,79 | 33052,6 | 0,0437 | 0,7 | 6 |
| 6 | 451 | 86,67 | 33262,3 | 0,1000 | 0,7 | 6 |
Récapitulatif du modèle
| Nombre total de prédicteurs | 34 |
|---|---|
| Prédicteurs importants | 24 |
| Nombre d'arbres développés | 500 |
| Nombre optimal d'arbres | 500 |
| Statistiques | Apprentissage | Test |
|---|---|---|
| R carré | 96,41% | 86,79% |
| Racine de l'erreur quadratique moyenne (RMSE) | 25035,7243 | 48029,9503 |
| Erreur quadratique moyenne (MSE) | 6,26787E+08 | 2,30688E+09 |
| Ecart absolu moyen (MAD) | 17309,3936 | 33052,6087 |
| Pourcentage d'erreur absolue moyen (MAPE) | 0,0930 | 0,1790 |
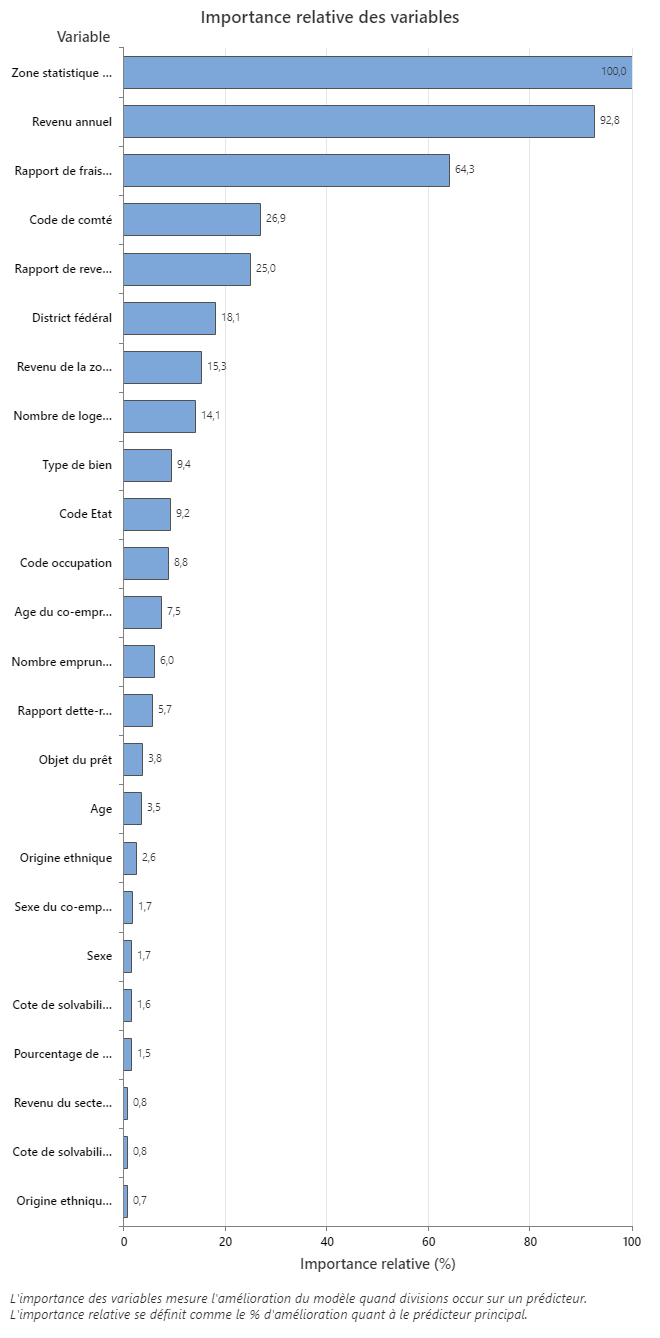
Le graphique Importance relative des variables trace les prédicteurs dans l’ordre de leur effet sur l’amélioration du modèle lorsque des divisions sont effectuées sur un prédicteur au cours de la séquence d’arbres. La variable prédictive la plus importante est la zone statistique basée sur la base. Si l’importance de la variable prédictive principale, la zone statistique de base, est de 100 %, la variable importante suivante, le revenu annuel, a une contribution de 92,8 %. Cela signifie que le revenu annuel de l’emprunteur est à 92,8% aussi important que la situation géographique du bien.
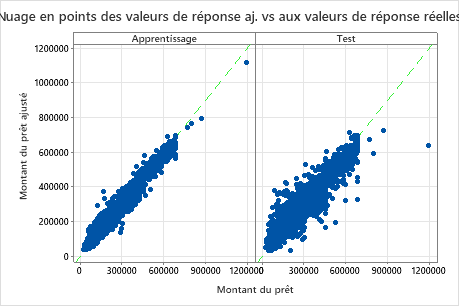
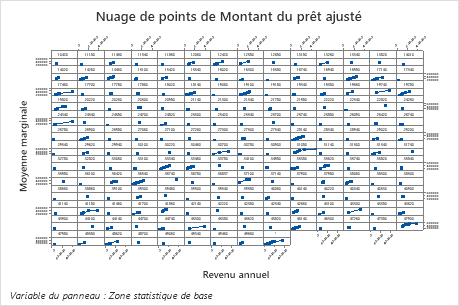
Le nuage de points entre les montants des prêts ajustés et les montants réels des prêts montre la relation entre les valeurs ajustées et réelles pour les données d’entraînement et les données de test. Vous pouvez survoler les points du graphique pour voir plus facilement les valeurs tracées. Dans cet exemple, tous les points se trouvent approximativement près de la droite de référence y=x.
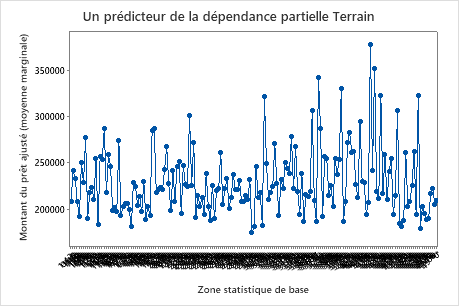
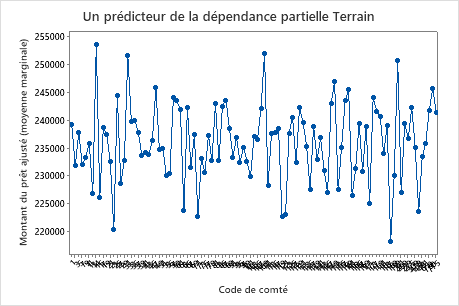
Utilisez les tracés de dépendances partielles pour obtenir des informations sur la façon dont les variables importantes ou les paires de variables affectent les valeurs de réponse ajustées. Les graphiques de dépendance partielle montrent si la relation entre la réponse et une variable est linéaire, monotone ou plus complexe.
Le premier graphique illustre le montant ajusté du prêt pour chaque domaine statistique de base. Étant donné qu’il y a beaucoup de points de données, vous pouvez survoler des points de données individuels pour voir les valeurs x et y spécifiques. Par exemple, le point le plus élevé sur le côté droit du graphique est pour la zone centrale numéro 41860 et le montant du prêt ajusté est d’environ 378069 $.
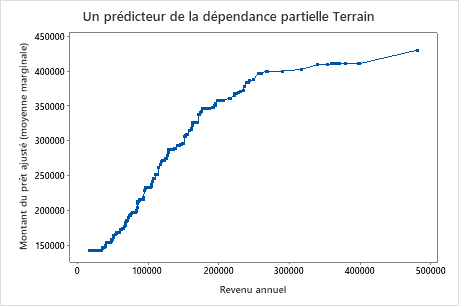
Le deuxième graphique montre que le montant du prêt ajusté augmente à mesure que le revenu annuel augmente. Une fois que le revenu annuel atteint 300000 $, les niveaux de montant du prêt ajusté augmentent à un rythme plus lent.
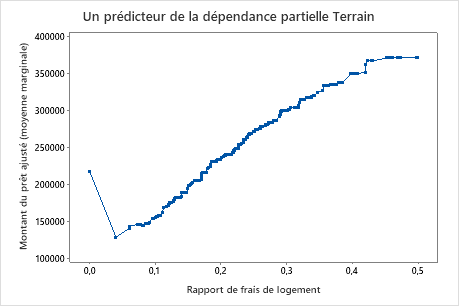
Le troisième graphique illustre que le montant du prêt ajusté augmente à mesure que le ratio à court terme augmente.
Le quatrième graphique illustre le montant du prêt ajusté pour chaque code de comté de recensement. Comme pour le premier graphique, vous pouvez survoler certains points de données pour obtenir plus d’informations. Sélectionnez ou pour produire des tracés pour d’autres variables.
