Remarque
Cette commande est disponible avec la commande Module d'analyse prédictive. Cliquez ici pour plus d’informations sur la façon d’activer le module.
Une équipe de chercheurs recueille des données sur les facteurs qui affectent une caractéristique de qualité des bretzels cuits au four. Les variables incluent les paramètres de processus, comme outil de mélange, et les propriétés de grain, comme protéine de farine.
Dans le cadre de l’exploration initiale des données, les chercheurs décident Découvrir les prédicteurs principaux de comparer les modèles en supprimant séquentiellement les prédicteurs sans importance pour identifier les prédicteurs clés. Les chercheurs espèrent identifier les prédicteurs clés qui ont des effets importants sur la caractéristique de qualité et obtenir plus de connaissances sur les relations entre la caractéristique de qualité et les prédicteurs clés.
- Ouvrez les données d’échantillonnage, acceptabilité_bretzel.MWX.
- Choisissez .
- Dans la liste déroulante, sélectionnez Réponse binaire.
- Dans Réponse, entrez 'bretzel acceptable'.
- Dans Evénement de réponse, sélectionnez 1 pour indiquer que le bretzel est acceptable.
- Dans Prédicteurs continus, entrez 'protéine de farine'-'densité en vrac'.
- Dans Prédicteurs de catégorie, entrez 'outil de mélange'-'méthode de four'.
- Cliquer Elimination des prédicteurs.
- Dans la Nombre maximal d’étapes d’élimination section 29.
- Cliquez dans OK chaque boîte de dialogue.
Interpréter les résultats
Pour cette analyse, Minitab Statistical Software compare 28 modèles. Le nombre d’étapes est inférieur au nombre maximal d’étapes, car le stabilité de mousse prédicteur a un score d’importance de 0 dans le premier modèle, de sorte que l’algorithme élimine 2 variables dans la première étape. L’astérisque dans la colonne Modèle de la table d’évaluation du modèle indique que le modèle avec la plus petite valeur de la statistique de log-vraisemblance moyenne est le modèle 23. Les résultats qui suivent le tableau d’évaluation du modèle concernent le modèle 23.
Bien que le modèle 23 ait la plus petite valeur de la statistique de log-vraisemblance moyenne, d’autres modèles ont des valeurs similaires. L’équipe peut cliquer Sélectionner un autre modèle pour produire des résultats pour d’autres modèles à partir du tableau d’évaluation du modèle.
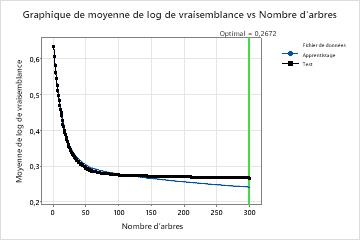
Dans les résultats du modèle 23, le graphique Log-vraisemblance moyenne en fonction du nombre d’arbres montre que le nombre optimal d’arbres est presque le nombre d’arbres dans l’analyse. L’équipe peut cliquer Régler les hyperparamètres pour augmenter le nombre d’arbres et voir si les modifications apportées à d’autres hyperparamètres améliorent les performances du modèle.
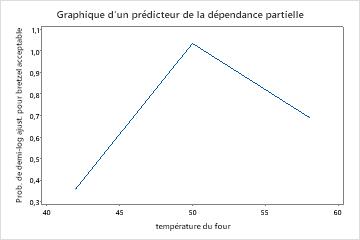
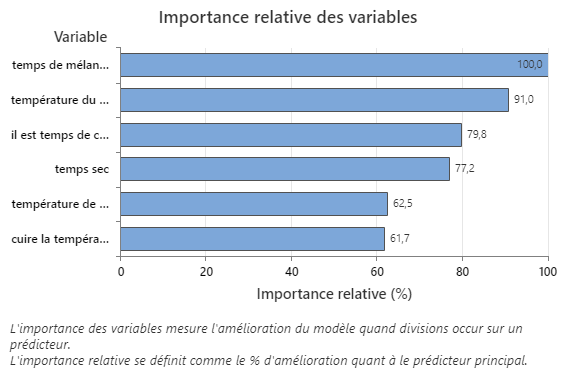
Le graphique Importance relative des variables trace les prédicteurs dans l’ordre de leur effet sur l’amélioration du modèle lorsque des divisions sont effectuées sur un prédicteur au cours de la séquence d’arbres. La variable prédictive la plus importante est temps de mélange. Si l’importance de la variable prédictive principale, temps de mélange, est de 100 %, la variable importante suivante, température du four, a une contribution de 91,0 %. Cela signifie que température du four est 91,0 % aussi important que temps de mélange.
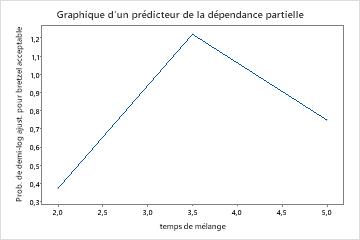
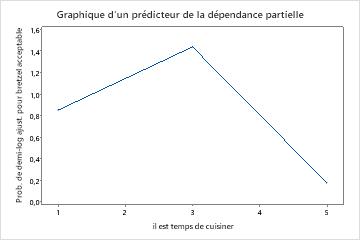
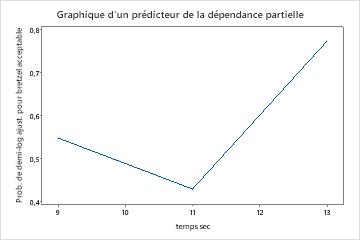
Utilisez les tracés de dépendances partielles pour obtenir des informations sur la façon dont les variables importantes ou les paires de variables affectent les valeurs de réponse ajustées. Les valeurs de réponse ajustées sont sur l’échelle 1/2 log. Les graphiques de dépendance partielle montrent si la relation entre la réponse et une variable est linéaire, monotone ou plus complexe.
Les graphiques de dépendance partielle d’un prédicteur montrent que des valeurs moyennes pour temps de mélange, température du four et il est temps de cuisiner augmentent les chances d’un bretzel acceptable. Une valeur moyenne de temps sec diminue les chances d’obtenir un bretzel acceptable. Les chercheurs peuvent choisir de produire des graphiques pour d’autres variables.
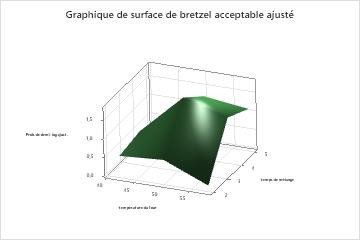
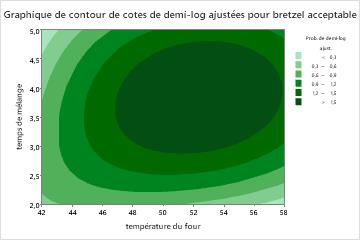
Le graphique de dépendance partielle à deux prédicteurs de temps de mélange et température du four montre une relation plus complexe entre les deux variables et la réponse. Alors que des valeurs moyennes de temps de mélange et température du four augmentent les chances d’un bretzel acceptable, le graphique montre que les meilleures chances se produisent lorsque les deux variables sont à des valeurs moyennes. Les chercheurs peuvent choisir de produire des graphiques pour d’autres paires de variables.
Méthode
| Critères de sélection du nombre d'arbres optimal | Log de vraisemblance maximale |
|---|---|
| Validation de modèle | Ensembles d'apprentissage/test 70/30% |
| Taux d'apprentissage | 0,05 |
| Méthode de sélection de sous-échantillon | Complètement aléatoire |
| Fraction de sous-échantillon | 0,5 |
| Nombre maximal de nœuds terminaux par arbre | 6 |
| Taille minimale du nœud terminal | 3 |
| Nombre de prédicteurs sélectionnés pour la partition des nœuds | Nombre total de prédicteurs = 29 |
| Lignes utilisées | 5000 |
Informations de réponse binaire
| Apprentissage | Test | ||||
|---|---|---|---|---|---|
| Variable | Classe | Dénombrement | % | Dénombrement | % |
| bretzel acceptable | 1 (Événement) | 2160 | 61,82 | 943 | 62,62 |
| 0 | 1334 | 38,18 | 563 | 37,38 | |
| Tous | 3494 | 100,00 | 1506 | 100,00 | |
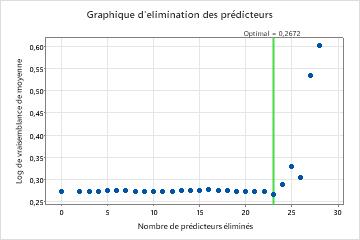
Sélection du modèle en éliminant les prédicteurs non importants
| Modèle | Nombre optimal d'arbres | Log de vraisemblance de moyenne | Nombre de prédicteurs | Prédicteurs éliminés |
|---|---|---|---|---|
| 1 | 268 | 0,273936 | 29 | Aucun |
| 2 | 268 | 0,274186 | 27 | stabilité de mousse; densité en vrac |
| 3 | 234 | 0,273843 | 26 | Min. concentration gélification |
| 4 | 233 | 0,274350 | 25 | mode four 2 |
| 5 | 232 | 0,274943 | 24 | méthode de four |
| 6 | 273 | 0,275553 | 23 | mode four 1 |
| 7 | 244 | 0,274811 | 22 | vitesse de mélange |
| 8 | 268 | 0,274258 | 21 | mode four 3 |
| 9 | 272 | 0,274185 | 20 | surface de repos |
| 10 | 232 | 0,274077 | 19 | cuire la température 3 |
| 11 | 287 | 0,273598 | 18 | outil de mélange |
| 12 | 227 | 0,274358 | 17 | cuire la température 1 |
| 13 | 276 | 0,275374 | 16 | temps de repos |
| 14 | 272 | 0,276082 | 15 | eau |
| 15 | 268 | 0,275595 | 14 | concentration caustique |
| 16 | 268 | 0,277810 | 13 | capacité d’enflure |
| 17 | 253 | 0,276436 | 12 | stabilité de l’émulsion |
| 18 | 231 | 0,276159 | 11 | activité d’émulsion |
| 19 | 268 | 0,273537 | 10 | capacité d’absorption de l’eau |
| 20 | 260 | 0,273455 | 9 | capacité d’absorption d’huile |
| 21 | 299 | 0,272848 | 8 | protéine de farine |
| 22 | 278 | 0,272629 | 7 | capacité de mousse |
| 23* | 299 | 0,267184 | 6 | taille de farine |
| 24 | 297 | 0,288621 | 5 | cuire la température 2 |
| 25 | 234 | 0,330342 | 4 | temps sec |
| 26 | 290 | 0,305993 | 3 | température de gélatinisation |
| 27 | 245 | 0,534345 | 2 | il est temps de cuisiner |
| 28 | 146 | 0,599837 | 1 | température du four |
Récapitulatif du modèle
| Nombre total de prédicteurs | 6 |
|---|---|
| Prédicteurs importants | 6 |
| Nombre d'arbres développés | 300 |
| Nombre optimal d'arbres | 299 |
| Statistiques | Apprentissage | Test |
|---|---|---|
| Log de vraisemblance de moyenne | 0,2418 | 0,2672 |
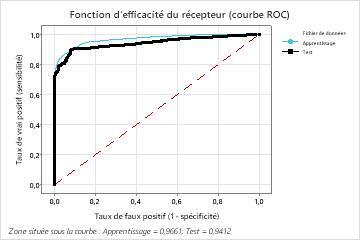
| Zone située sous la courbe ROC | 0,9661 | 0,9412 |
| IC à 95 % | (0,9608; 0,9713) | (0,9295; 0,9529) |
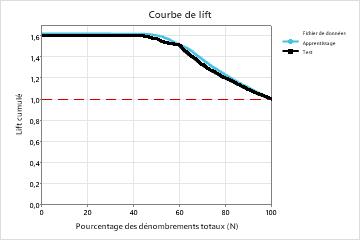
| Lift | 1,6176 | 1,5970 |
| Taux de mauvaise classification | 0,0970 | 0,0963 |
Matrice de confusion
| Classe prévue (apprentissage) | Classe prévue (test) | |||||||
|---|---|---|---|---|---|---|---|---|
| Classe réelle | Dénombrement | 1 | 0 | % correct | Dénombrement | 1 | 0 | % correct |
| 1 (Événement) | 2160 | 1942 | 218 | 89,91 | 943 | 846 | 97 | 89,71 |
| 0 | 1334 | 121 | 1213 | 90,93 | 563 | 48 | 515 | 91,47 |
| Tous | 3494 | 2063 | 1431 | 90,30 | 1506 | 894 | 612 | 90,37 |
| Statistiques | Apprentissage (%) | Test (%) |
|---|---|---|
| Taux de vrai positif (sensibilité ou puissance) | 89,91 | 89,71 |
| Taux de faux positif (erreur de type I) | 9,07 | 8,53 |
| Taux de faux négatif (erreur de type II) | 10,09 | 10,29 |
| Taux de vrai négatif (spécificité) | 90,93 | 91,47 |
Mauvais classement
| Apprentissage | Test | |||||
|---|---|---|---|---|---|---|
| Classe réelle | Dénombrement | Mal classé | % erreur | Dénombrement | Mal classé | % erreur |
| 1 (Événement) | 2160 | 218 | 10,09 | 943 | 97 | 10,29 |
| 0 | 1334 | 121 | 9,07 | 563 | 48 | 8,53 |
| Tous | 3494 | 339 | 9,70 | 1506 | 145 | 9,63 |