Remarque
Cette commande est disponible avec le Module d'analyse prédictive. Cliquez ici pour plus d'informations sur l'activation du module.
Une équipe de chercheurs recueille des données sur la vente de propriétés résidentielles individuelles à Ames, iowa. Les chercheurs veulent identifier les variables qui influent sur le prix de vente. Les variables incluent la surface du terrain et diverses caractéristiques de la propriété résidentielle.
Après une première exploration à l'aide de Régression CART® pour identifier les prédicteurs importants, l'équipe utilise Régression Random Forests® pour créer un modèle plus avancés à partir du même ensemble de données. L'équipe compare le tableau récapitulatif du modèle et la courbe R2 dans les résultats pour évaluer quel modèle fournit un meilleur résultat de prédiction.
Ces données ont été adaptées à partir d'un ensemble de données public contenant des informations sur les données sur le logement d'Ames. Données originales de DeCock, Truman State University.
- Ouvrez l’exemple de données Ames_logement.MWX.
- Sélectionnez .
- Dans la zone Réponse, saisissez ‘prix de vente’.
- Dans Prédicteurs continus, entrez ‘façade de lot' – ‘année vendue’.
- Dans Prédicteurs de catégorie, entrez ‘type' – ‘condition de vente’.
- Cliquez sur Options.
- Sous Nombre de prédicteurs pour la partition des nœuds, sélectionnez K pour cent du nombre total de prédicteurs ; K = et saisissez 30. Les chercheurs veulent utiliser plus que le nombre par défaut de prédicteurs pour cette analyse.
- Cliquez sur OK dans chaque boîte de dialogue
Interpréter des résultats
Méthode
| Validation de modèle | Validation avec données out-of-bag |
|---|---|
| Nombre d'échantillons bootstrap | 300 |
| Effectif d'échantillon | Identique à la taille des données d'apprentissage de 2930 |
| Nombre de prédicteurs sélectionnés pour la partition des nœuds | 30% du nombre total de prédicteurs = 23 |
| Taille minimale du nœud interne | 5 |
| Lignes utilisées | 2930 |
Informations de réponse
| Moyenne | EcTyp | Minimum | Q1 | Médiane | Q3 | Maximum |
|---|---|---|---|---|---|---|
| 180796 | 79886,7 | 12789 | 129500 | 160000 | 213500 | 755000 |
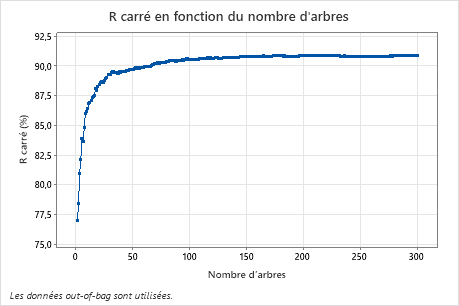
Le diagramme du R carré par rapport au nombre d'arbres montre toute la courbe sur le nombre d'arbres développés. La valeur de R2 augmente rapidement à mesure que le nombre d’arbres augmente, puis s’aplatit à environ 91%.
Récapitulatif du modèle
| Nombre total de prédicteurs | 77 |
|---|---|
| Prédicteurs importants | 68 |
| Statistiques | Out-of-Bag |
|---|---|
| R carré | 90,90% |
| Racine de l'erreur quadratique moyenne (RMSE) | 24097,3281 |
| Erreur quadratique moyenne (MSE) | 5,80681E+08 |
| Ecart absolu moyen (MAD) | 14746,8323 |
| Pourcentage d'erreur absolue moyen (MAPE) | 0,0895 |
Le tableau récapitulatif du modèle montre que les valeurs R2 sont légèrement améliorées par rapport aux valeurs R2 de l'analyse CART® correspondante.

La courbe d'importance relative des variables trace les prédicteurs dans l'ordre de leur effet sur l'amélioration du modèle lorsqu'un prédicteur est divisé sur la séquence des arbres. La variable de prédiction la plus importante pour prédire le prix de vente est la qualité. Si l’importance de la variable prédictive supérieure, la qualité, est de 100%, alors la variable importante suivante, zone de vie, a une contribution de 88,8%. Cela signifie que la superficie en pieds carrés de la vie est 88,8% aussi importante que la qualité globale de la propriété. La deuxième variable la plus importante est le voisinage, qui a une contribution de 52,6%.
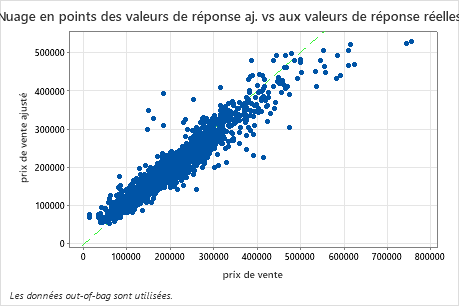
Le nuage de points du prix de vente ajusté en fonction du prix de vente réel montre la relation entre les valeurs ajustées et réelles pour les données out-of-bag. Pour identifier plus facilement les valeurs représentées, survolez les points du graphique. Dans cet exemple, de nombreux points se situent approximativement près de la ligne de référence de y=x, mais plusieurs points peuvent nécessiter une enquête pour voir des écarts entre les valeurs ajustées et réelles.
