Remarque
Cette commande est disponible avec le Module d'analyse prédictive. Cliquez ici pour plus d'informations sur l'activation du module.
Variables importantes
Minitab Statistical Software offre deux méthodes pour classer l’importance des variables.
Permutation
- A = 87
- B = 9
- C = 4
La marge pour cette ligne est alors de 0,87 - 0,09 = 0,78.
La marge out-of-bag moyenne est la marge moyenne pour toutes les lignes de données.
Pour connaître l'importance de la variable, permutez aléatoirement les valeurs d'une variable, xm dans les données out-of-bag. Laissez identiques les valeurs de réponse et les valeurs des autres prédicteurs. Procédez ensuite de même pour calculer la marge moyenne des données permutées, 
.
L’importance de la variable xm vient de la différence des deux moyennes :
où 
est la marge moyenne avant la permutation. Minitab arrondit les valeurs inférieures à 10-7 à 0.
Gini
Tout arbre de classification est une collection de divisions. Chaque division apporte une amélioration à l'arbre.
La formule suivante donne l'amélioration à un seul nœud :
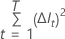
où 
est le nombre de nœuds qui se divisent et 
pour n’importe quel nœud 
où la variable d’intérêt n’est pas le séparateur.
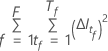
Où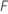 
est le nombre d'arbres dans la forêt et 
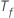est le nombre de nœuds qui se divisent dans l'arbre 
.
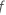Le calcul de l’impureté des nœuds est comparable à celui de la méthode Gini. Pour plus de détails sur la méthode Gini, reportez-vous à Méthodes de partition des nœud dans Classification CART®.
Moyenne du log négatif de vraisemblance
Données out-of-bag
Le calcul utilise les échantillons out-of-bag de chaque arbre de la forêt. En raison de la nature des échantillons out-of-bag, attendez-vous à utiliser différentes combinaisons d’arbres pour trouver la contribution au log de vraisemblance de chaque ligne dans les données.
Pour un arbre donné dans la forêt, un vote de classe pour une ligne dans les données out-of-bag est la classe prévue pour la ligne d'après l'arbre unique. La classe prévue pour une ligne dans les données out-of-bag est la classe de vote le plus élevé sur tous les arbres de la forêt. La probabilité de classe prévue pour une ligne dans les données out-of-bag est le rapport entre le nombre de votes pour la classe et le total des votes pour la ligne. Les calculs de vraisemblance suivent ces probabilités :
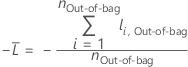
où
et 
est la probabilité d’événement calculée pour la ligne i dans les données out-of-bag.
Notation pour données out-of-bag
| Terme | Description |
|---|---|
| nOut-of-bag | nombre de lignes qui sont out-of-bag au moins une fois |
| yi, Out-of-bag | valeur de réponse binaire du cas i dans les données out-of-bag. yi, Out-of-bag = 1 pour la classe de l'événement, et 0 autrement. |
Ensemble de test
Pour un arbre donné dans la forêt, un vote de classe pour une ligne dans le fichier de test est la classe prévue pour la ligne de l’arbre unique. La classe prévue pour une ligne dans l’ensemble de test est la classe avec le vote le plus élevé sur tous les arbres dans la forêt. La probabilité de classe prévue pour une ligne dans l'ensemble de test est le rapport entre le nombre de votes pour la classe et le total des votes pour la ligne. Les calculs de vraisemblance suivent ces probabilités :
où
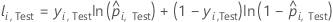
Notation pour l’ensemble de test
| Terme | Description |
|---|---|
| nTest | effectif de l’échantillon de l’ensemble de test |
| yi, Test | valeur de réponse binaire du cas i dans l'ensemble de test. yi, k = 1 pour la classe d'événement, et 0 autrement. |
 | probabilité d’événement prévue pour le cas i dans l’ensemble de test |
Aire sous la courbe ROC
Formule
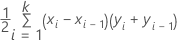
où k est le nombre de probabilités d'événements distinctes et (x0, y0) est le point (0, 0).
Pour calculer l'aire d'une courbe à partir données out-of-bag d'un ensemble de test, utilisez les points de la courbe correspondante.
Notation
| Terme | Description |
|---|---|
| TPR | taux de vrais positifs |
| FPR | taux de faux positifs |
| TP | vrais positifs, événements qui ont été correctement évalués |
| FN | faux négatifs, événements qui ont été mal évalués |
| P | nombre d’événements positifs réels |
| FP | faux positifs, non-événements qui ont été mal évalués |
| N | nombre d’événements négatifs réels |
| FNR | taux de faux négatifs |
| TNR | taux de vrais négatifs |
Exemple
| X (taux de faux positifs) | Y (taux de vrais positifs) |
|---|---|
| 0,0923 | 0,3051 |
| 0,4154 | 0,7288 |
| 0,7538 | 0,9322 |
| 1 | 1 |
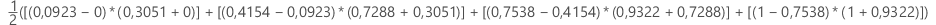
IC à 95 % pour l'aire sous la courbe ROC
L’intervalle suivant donne les limites supérieure et inférieure de l’intervalle de confiance :
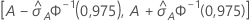
Le calcul de l'erreur type de l'aire sous la courbe ROC (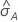
) provient de Salford Predictive Modeler®. Pour obtenir des informations générales sur l’estimation de la variance de l'aire située sous la courbe ROC, consultez les références suivantes :
Engelmann, B. (2011). Measures of a ratings discriminative power: Applications and limitations, Dans B. Engelmann et R. Rauhmeier (Eds.), The Basel II Risk Parameters:Estimation, Validation, Stress Testing - With Applications to Loan Risk Management (2e éd.) Heidelberg ; New York : Springer. doi :10.1007/978-3-642-16114-8
Cortes, C. et Mohri, M. (2005). Confidence intervals for the area under the ROC curve. Advances in neural information processing systems, 305-312.
Feng, D., Cortese, G. et Baumgartner, R. (2017). A comparison of confidence/credible interval methods for the area under the ROC curve for continuous diagnostic tests with small sample size. Statistical Methods in Medical Research, 26(6), 2603-2621. doi :10.1177/0962280215602040
Notation
| Terme | Description |
|---|---|
| A | aire située sous la courbe ROC |
 | 0,975 percentile de la loi normale standard |
Lift
Pour consulter les calculs généraux du lift cumulé, accédez à Méthodes et formules pour la courbe de lift cumulé dans Classification Random Forests®.
Taux de mauvais classement
L’équation suivante donne le taux de mauvais classement :
Le nombre de cas mal classés est le nombre de lignes dans les données out-of-bag dont les classes prévues sont différentes de leurs classes réelles. Le dénombrement total est le nombre total de lignes dans les données out-of-bag.
Pour validation avec un ensemble de données de test, le nombre de cas mal classés est la somme des erreurs de classement dans l’ensemble de test. Le dénombrement total est le nombre de lignes dans l'ensemble de données de test.
