Remarque
Cette commande est disponible avec le Module d'analyse prédictive. Cliquez ici pour plus d'informations sur l'activation du module.
Régression MARS® construit essentiellement des modèles flexibles en ajustant des régressions linéaires par morceaux. Le modèle a la restriction que les extrémités des lignes par morceaux se rejoignent uniformément. Les approximations de la non-linéarité des modèles utilisent des pentes de régression distinctes à des intervalles distincts des données. Une approximation du processus est facile à visualiser dans le cas simple en 2 dimensions.
Dans le cas à 2 dimensions, une seule ligne droite s’adapte aux données. Ce modèle fournit une base de référence pour tester l’amélioration de l’ajout de complexité supplémentaire.
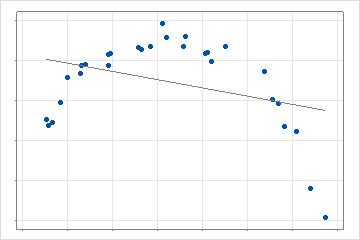
Dans l’étape suivante, l’analyse recherche la valeur d’un prédicteur qui crée une fonction de base qui conduit à la plus grande amélioration du critère de recherche. Le calcul du critère dépend de la sélection pour l’analyse et de la méthode de validation. Dans le cas à 2 dimensions, ce modèle est une régression linéaire par morceaux avec 2 lignes au lieu de 1 ligne. Avec plusieurs prédicteurs, la recherche du meilleur point de données évalue chaque prédicteur autorisé par l’analyse.
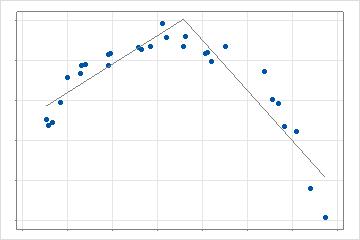
Une fois que l’analyse a trouvé la première valeur qui fournit la meilleure amélioration, l’analyse recherche les valeurs de prédicteur restantes pour trouver la meilleure amélioration par rapport au modèle actuel. Dans le cas à 2 dimensions, ce modèle comporte 3 lignes qui décrivent différentes parties des données. La recherche se répète jusqu’au nombre maximal de fonctions de base pour l’analyse. Lorsque les interactions sont autorisées, l’analyse effectue des séries supplémentaires de recherches en multipliant les fonctions de base candidates par d’autres fonctions de base déjà présentes dans le modèle.
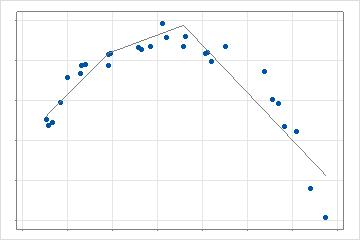
Une fois que l’analyse a rapidement ajusté le nombre maximal de fonctions de base et estimé les paramètres de ces fonctions, l’analyse identifie le nombre optimal de fonctions de base. Le nombre optimal de fonctions de base utilise une approche d’élimination progressive et rétrospective pour trouver le nombre de fonctions de base avec la meilleure valeur du critère d’optimalité.
Valeurs manquantes pour l’ajustement du modèle
Dans la recherche des fonctions de base, Régression MARS® crée des variables d’indicateur pour tous les prédicteurs avec des valeurs manquantes. La variable indicateur indique si une valeur du prédicteur est manquante. Si l’analyse inclut une fonction de base pour un prédicteur avec des valeurs manquantes dans le modèle, le modèle inclut également une fonction de base pour la variable indicateur. Les autres fonctions de base du prédicteur interagissent toutes avec la fonction de base de la variable indicateur.
Lorsqu’un prédicteur a une valeur manquante, la fonction de base de la variable indicateur annule les autres fonctions de base de ce prédicteur par multiplication par 0. Ces fonctions de base pour les valeurs manquantes se trouvent dans tous les modèles où des prédicteurs importants ont des valeurs manquantes, même les modèles additifs et les modèles qui désactivent d’autres types de transformations.
Valeurs manquantes pour la prédiction
Régression MARS® Calcule les prédictions lorsque les prédicteurs du modèle ont des valeurs manquantes. L’analyse utilise différentes stratégies selon que des valeurs manquantes pour le prédicteur étaient présentes ou non lorsque l’analyse correspondait au modèle. Si des valeurs manquantes pour le prédicteur étaient présentes lorsque l’analyse ajustait le modèle, les fonctions de base du modèle incluent une variable indicateur qui supprime le prédicteur du modèle lorsque le prédicteur a une valeur manquante.
Le deuxième cas est lorsque les valeurs de prédiction incluent des valeurs manquantes pour un prédicteur, mais que le prédicteur n’avait pas de valeurs manquantes lorsque l’analyse correspondait au modèle. Pour calculer les prédictions dans ce cas, l’analyse impute la valeur manquante. Pour un prédicteur continu, la moyenne du prédicteur remplace la valeur manquante. Pour un prédicteur catégoriel, la valeur finale non manquante dans l’ensemble de données remplace la valeur manquante.
