Sur ce thème
Etape 1 : Déterminer l'ajustement du modèle à vos données
- R carré
- Plus la valeur de R2 est élevée, plus l'ajustement offert par le modèle est bon. R2 est toujours compris entre 0% et 100%. Les valeurs aberrantes ont un effet plus important sur R2 que sur le MAD.
- Erreur quadratique moyenne de la racine de test (RMSE)
- Des valeurs plus petites indiquent un meilleur ajustement. Les valeurs aberrantes ont un effet plus important sur le RMSE que sur le MAD.
- Erreur quadratique moyenne du test (MSE)
- Des valeurs plus petites indiquent un meilleur ajustement. Les valeurs aberrantes ont un effet plus important sur le MSE que sur le MAD.
- Écart absolu moyen d’essai (MAD)
- Des valeurs plus petites indiquent un meilleur ajustement. L'écart absolu moyen (MAD) exprime l'exactitude dans les mêmes unités que les données, ce qui permet de conceptualiser la quantité d'erreurs. Les valeurs aberrantes ont moins d'effet sur le MAD que sur le R2, la RMSE et la MSE.
Récapitulatif du modèle
| Nombre total de prédicteurs | 77 |
|---|---|
| Prédicteurs importants | 10 |
| Nombre maximal de fonctions de base | 30 |
| Nombre optimal de fonctions de base | 13 |
| Statistiques | Apprentissage | Test |
|---|---|---|
| R carré | 89,61% | 87,61% |
| Racine de l'erreur quadratique moyenne (RMSE) | 25836,5197 | 27855,6550 |
| Erreur quadratique moyenne (MSE) | 667525749,7185 | 775937512,8264 |
| Ecart absolu moyen (MAD) | 17506,0038 | 17783,5549 |
Principaux résultats : Test R-carré, Erreur quadratique moyenne du test (RMSE), Erreur quadratique moyenne du test (MSE), Écart absolu moyen du test (MAD)
Dans ces résultats, le test R-carré est d’environ 88%. L’erreur quadratique moyenne de la racine de test est d’environ 27 856. L’erreur quadratique moyenne du test est d’environ 775 937 513. L’écart absolu moyen du test est d’environ 17 784.
Etape 2 : Déterminer quelles variables sont les plus importantes pour le modèle
Utilisez le graphique d’importance relative des variables pour voir quels prédicteurs sont les variables les plus importantes pour le modèle.
Les variables importantes sont dans au moins 1 fonction de base dans le modèle. La variable avec le score d'amélioration le plus élevé est la variable la plus importante et les autres variables sont classées en conséquence. L'importance relative des variables normalise les valeurs d'importance pour faciliter l'interprétation. L'importance relative se définit comme l'amélioration en pourcentage par rapport au prédicteur le plus important.
Les valeurs d’importance relative des variables varient de 0 % à 100 %. La variable la plus importante a toujours une importance relative de 100%. Si une variable n’est pas dans une fonction de base, cette variable n’est pas importante.
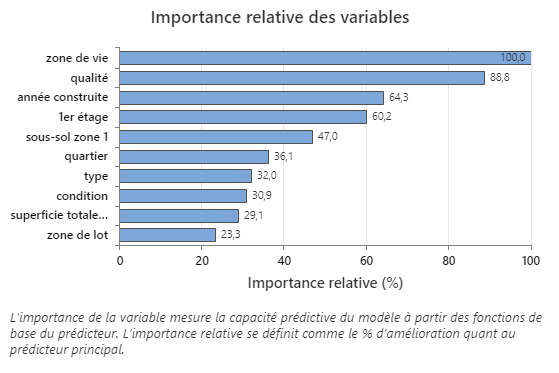
Principal résultat : Importance relative des variables
- qualité est environ 89% aussi important que zone de vie.
- année construite est environ 64% aussi important que zone de vie.
- 1er étage est environ 60% aussi important que zone de vie.
Bien que ces résultats comprennent 10 variables d'importance positive, les classements relatifs fournissent des informations sur le nombre de variables à contrôler ou à surveiller pour une certaine application. Les baisses abruptes des valeurs d'importance relative d'une variable à la suivante peuvent guider les décisions sur les variables à contrôler ou à surveiller. Par exemple, dans ces données, les 2 variables les plus importantes ont des valeurs d’importance relativement proches les unes des autres avant une baisse de plus de 20% de l’importance relative par rapport à la variable suivante. De même, 2 variables ont des valeurs d’importance similaires supérieures à 60%. Vous pouvez supprimer les variables de différents groupes et refaire l'analyse pour évaluer l'impact des variables de différents groupes sur les valeurs d'exactitude de prévision dans le tableau récapitulatif du modèle.
Etape 3 : Explorer les effets des prédicteurs
Utilisez les diagrammes de dépendance partielle, les fonctions de base et les coefficients de l’équation de régression pour déterminer l’effet des prédicteurs. Les effets des prédicteurs expliquent la relation entre les prédicteurs et la réponse. Considérez toutes les fonctions de base d’un prédicteur pour comprendre l’effet du prédicteur sur la variable de réponse.
En outre, tenez compte de l’utilisation des prédicteurs importants et des formes de leurs relations lorsque vous construisez d’autres modèles. Par exemple, si le modèle de régression MARS® inclut des interactions, déterminez s’il faut inclure ces interactions dans un modèle de régression des moindres carrés pour comparer les performances des deux types de modèles. Dans les applications où vous contrôlez les prédicteurs, les effets fournissent un moyen naturel d’optimiser les paramètres pour atteindre un objectif pour la variable de réponse.
Dans un modèle additif, des diagrammes de dépendance partielle à un prédicteur montrent comment les prédicteurs continus importants affectent la réponse prédite. Le diagramme de dépendance partielle à un prédicteur indique comment la réponse est censée changer avec les modifications apportées aux niveaux des prédicteurs. Pour Régression MARS®, les valeurs du tracé proviennent des fonctions de base du prédicteur sur l’axe des abscisses. La contribution sur l’axe des y est normalisée de sorte que la valeur minimale sur la parcelle soit 0.
Principal résultat : Diagramme de dépendance partielle
Ce graphique illustre cette augmentation à mesure que prix de vente la zone de vie superficie minimale en pieds carrés dans l’ensemble de données passe d’environ 3 000 pieds carrés. Après zone de vie avoir atteint 3 000 pieds carrés, la contribution à prix de vente devient stable à environ 152 000 $.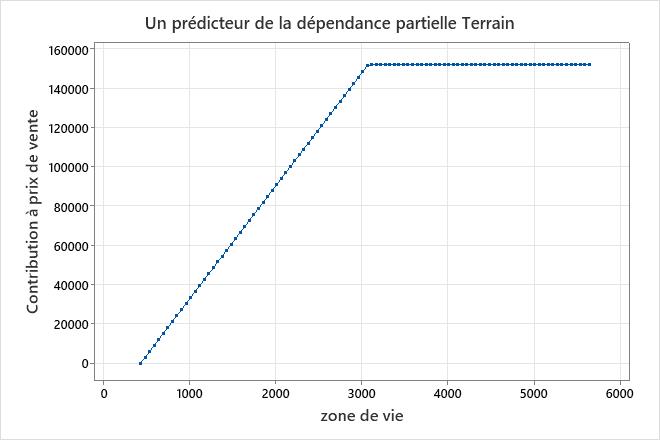
Equation de régression
BF3 = lorsque qualité est 8; 9; 10
BF6 = max(0, 2002 - année construite)
BF7 = lorsque sous-sol zone 1 n'est pas manquant
BF10 = max(0, 1696 - sous-sol zone 1) * BF7
BF11 = lorsque qualité est 1; 8
BF13 = lorsque type est 90; 150; 160; 180; 190
BF15 = lorsque quartier est Bluestem; Clear Creek; Collines vertes; Crawford; Northridge;
Northridge Heights; Point de repère; Pont de pierre; Timberland; Veenker; Villages Somerset
BF17 = lorsque superficie totale du sous-sol n'est pas manquant
BF19 = max(0, superficie totale du sous-sol - 1392) * BF17
BF21 = max(0, 1er étage - 2402)
BF23 = lorsque condition est 1; 2; 3; 4; 5; 6
BF25 = lorsque qualité est 1; 7; 10
BF27 = max(0, 1er étage - 2207)
BF30 = max(0, 15138 - zone de lot)
prix de vente = 325577 - 57,6167 * BF2 + 115438 * BF3 - 605,079 * BF6 - 25,3989 * BF10 -
66735,2 * BF11 - 23688,9 * BF13 + 22374,5 * BF15 + 50,3801 * BF19 - 576,789 * BF21 - 18099,2
* BF23 + 22414,2 * BF25 + 361,254 * BF27 - 1,82 * BF30
Résultat clé : Equation de régression
Dans ces résultats, BF2 a un coefficient négatif dans l’équation de régression. Le coefficient de la fonction de base est −57,6167. La disposition de la fonction de base est max(0, c - X). Dans cet arrangement, la valeur de la fonction de base diminue lorsque le prédicteur augmente. La combinaison de cet arrangement et du coefficient négatif crée une relation positive entre la variable prédictive et la variable de réponse. La pente de est de 57,6167 de zone de vie 438 à 3 078.
Pour plus d’exemples de fonctions de base courantes, reportez-vous à Équation de régression pour Régression MARS®la section .
