Remarque
Cette commande est disponible avec le Module d'analyse prédictive. Cliquez ici pour plus d'informations sur l'activation du module.
y = b0 + b1BF1+ b2BF2+ ... + bkBFk
- y est la variable de réponse
- b0 est le terme constant
- b1 + b2 + ... + bk sont des coefficients pour les fonctions de base
- BF1 + BF2 + ... + BFk sont les fonctions de base
Résolvez les fonctions de base des valeurs du prédicteur pour calculer la valeur prédite de la réponse.
Fonctions de base
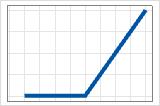
- max(0, X − c)
- Coefficient positif
- La contribution est de 0 jusqu’à c, puis augmente.
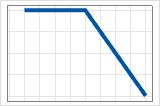
- max(0, X − c)
- Coefficient négatif
- La contribution est la contribution maximale jusqu’à c, puis diminue.
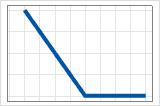
- max(0, c − X)
- Coefficient positif
- La cotisation commence au maximum et diminue jusqu’à c. Après c, la contribution est égale à 0.
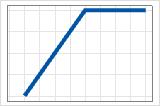
- max(0, c − X)
- Coefficient négatif
- La cotisation commence à 0 et augmente jusqu’à c. Après c, les cotisations sont à la valeur maximale.
Si c est égal à la valeur minimale ou maximale du prédicteur, alors le prédicteur a le même effet pour toutes les valeurs de la fonction de base. Le diagramme de dépendance partielle pour ces 2 cas montre une ligne droite. Régression MARS® fait de C l’un des points d’extrémité d’une analyse qui interdit les transformations pour le prédicteur.
Pour les prédicteurs catégoriels, les fonctions de base sont des fonctions d’indicateur. La fonction a une valeur de 0 pour certaines catégories et une valeur de 1 pour les autres catégories. Les fonctions de base ont la forme suivante :
Lorsque X est x1, ... xk où k est le nombre de niveaux dans la fonction de base ,k ≥ 1.
La valeur de la fonction est 1 pour les catégories de la fonction de base. La multiplication de la fonction de base par le coefficient dans l’équation de régression détermine l’effet lorsque la fonction passe de 0 à 1.
Exemple de prédicteur continu dans 1 fonction de base
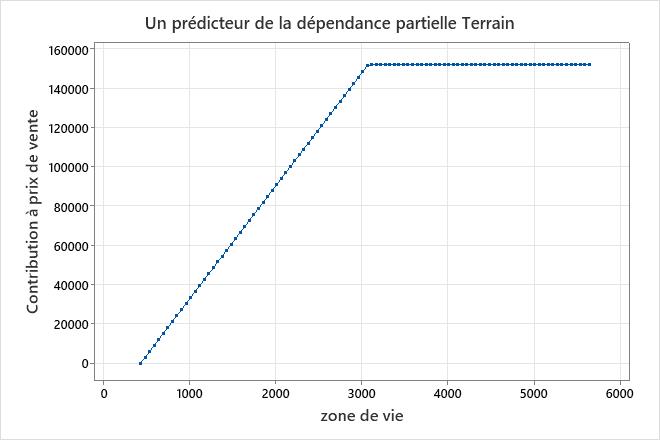
Dans ces résultats, BF2 a un coefficient négatif dans l’équation de régression. Le coefficient de la fonction de base est −57,6167. La disposition de la fonction de base est max(0, c − X). Dans cet arrangement, la valeur de la fonction de base diminue lorsque le prédicteur augmente. La combinaison de cet arrangement et du coefficient négatif crée une relation positive entre la variable prédictive et la variable de réponse. L’effet de est d’augmenter zone de vie dans la région de prix de vente 438 à 3 078. La pente de est de 57,6167 de zone de vie 438 à 3 078.
Equation de régression
BF3 = lorsque qualité est 8; 9; 10
BF6 = max(0, 2002 - année construite)
BF7 = lorsque sous-sol zone 1 n'est pas manquant
BF10 = max(0, 1696 - sous-sol zone 1) * BF7
BF11 = lorsque qualité est 1; 8
BF13 = lorsque type est 90; 150; 160; 180; 190
BF15 = lorsque quartier est Bluestem; Clear Creek; Collines vertes; Crawford; Northridge;
Northridge Heights; Point de repère; Pont de pierre; Timberland; Veenker; Villages Somerset
BF17 = lorsque superficie totale du sous-sol n'est pas manquant
BF19 = max(0, superficie totale du sous-sol - 1392) * BF17
BF21 = max(0, 1er étage - 2402)
BF23 = lorsque condition est 1; 2; 3; 4; 5; 6
BF25 = lorsque qualité est 1; 7; 10
BF27 = max(0, 1er étage - 2207)
BF30 = max(0, 15138 - zone de lot)
prix de vente = 325577 - 57,6167 * BF2 + 115438 * BF3 - 605,079 * BF6 - 25,3989 * BF10 -
66735,2 * BF11 - 23688,9 * BF13 + 22374,5 * BF15 + 50,3801 * BF19 - 576,789 * BF21 - 18099,2
* BF23 + 22414,2 * BF25 + 361,254 * BF27 - 1,82 * BF30
Un diagramme de dépendance partielle du prédicteur
Dans un modèle additif, utilisez les diagrammes de dépendance partielle à un prédicteur pour mieux comprendre comment les prédicteurs continus importants affectent la réponse prédite. Le diagramme de dépendance partielle à un prédicteur indique comment la réponse est censée changer avec les modifications apportées aux niveaux des prédicteurs. Pour Régression MARS®, les valeurs du tracé proviennent des fonctions de base du prédicteur sur l’axe des abscisses. La contribution sur l’axe des y est normalisée de sorte que la valeur minimale sur la parcelle soit 0.
Ce graphique illustre cette augmentation à mesure que prix de vente la zone de vie superficie minimale en pieds carrés dans l’ensemble de données passe d’environ 3 000 pieds carrés. Après zone de vie avoir atteint 3 000 pieds carrés, la contribution à prix de vente devient stable à environ 152 000 $.
Exemple de prédicteur catégorique dans 1 fonction de base
Dans ces résultats, BF3 est pour le prédicteur qualité. La fonction de base est pour lorsque la valeur de qualité est 8, 9 ou 10. Le coefficient BF3 dans l’équation est 115 438. Cette fonction de base indique que lorsque la valeur de la qualité passe d’une valeur de 1 à 7 à une valeur de 8, 9 ou 10, le prix de vente augmente de 115 438 $ dans le modèle. qualité est également dans BF11 et BF25. Pour comprendre l’effet du prédicteur sur la variable de réponse, considérez toutes les fonctions de base.
Equation de régression
BF3 = lorsque qualité est 8; 9; 10
BF6 = max(0, 2002 - année construite)
BF7 = lorsque sous-sol zone 1 n'est pas manquant
BF10 = max(0, 1696 - sous-sol zone 1) * BF7
BF11 = lorsque qualité est 1; 8
BF13 = lorsque type est 90; 150; 160; 180; 190
BF15 = lorsque quartier est Bluestem; Clear Creek; Collines vertes; Crawford; Northridge;
Northridge Heights; Point de repère; Pont de pierre; Timberland; Veenker; Villages Somerset
BF17 = lorsque superficie totale du sous-sol n'est pas manquant
BF19 = max(0, superficie totale du sous-sol - 1392) * BF17
BF21 = max(0, 1er étage - 2402)
BF23 = lorsque condition est 1; 2; 3; 4; 5; 6
BF25 = lorsque qualité est 1; 7; 10
BF27 = max(0, 1er étage - 2207)
BF30 = max(0, 15138 - zone de lot)
prix de vente = 325577 - 57,6167 * BF2 + 115438 * BF3 - 605,079 * BF6 - 25,3989 * BF10 -
66735,2 * BF11 - 23688,9 * BF13 + 22374,5 * BF15 + 50,3801 * BF19 - 576,789 * BF21 - 18099,2
* BF23 + 22414,2 * BF25 + 361,254 * BF27 - 1,82 * BF30
Remarque
Dans une équation de régression traditionnelle, le coefficient de l’équation de régression représente toujours le changement de 0 à 1. Dans Régression MARS®, le coefficient peut représenter le passage de 1 à 0. Considérons une variable catégorique binaire qui est 0 lorsqu’un patient déclare qu’il n’a pas mal à la tête et 1 lorsqu’un patient signale qu’il a mal à la tête. Supposons que le prédicteur ait la fonction de base suivante :
- BF1 = lorsque le mal de tête est égal à 0
Fonctions de base multiples pour 1 prédicteur
Régression MARS® utilise plusieurs fonctions de base pour un seul prédicteur afin de modéliser des relations non linéaires plus complexes entre un prédicteur et la réponse. Des fonctions de base supplémentaires créent des changements supplémentaires dans la pente de la relation entre le prédicteur et la variable de réponse. Régression MARS® Permet des prédicteurs dans plusieurs fonctions de base dans des modèles additifs.
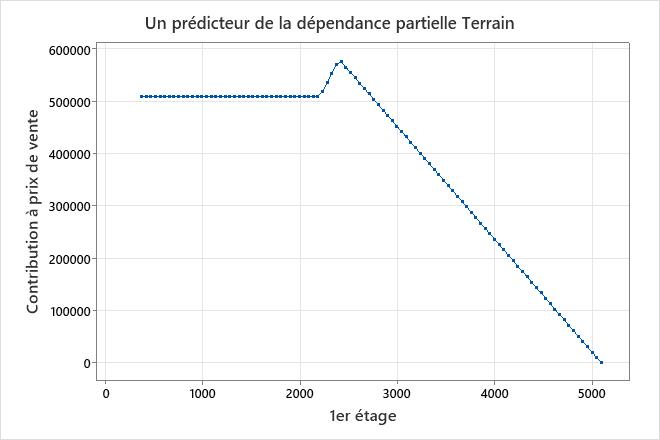
Dans ces résultats, BF21 est pour le prédicteur 1er étage. La fonction de base BF27 est également pour 1er étage. BF21 et BF27 ont tous deux le même arrangement, max(0, X − c). Les fonctions de base de cet arrangement affectent la variable de réponse lorsque le prédicteur a une valeur supérieure à c. Pour 2 fonctions de base avec cet arrangement, aucune des deux fonctions de base n’affecte la réponse jusqu’à ce que le prédicteur atteigne la valeur minimale dans 1 des fonctions de base. Dans ces résultats, cette valeur est de 2 207 dans BF27. 1er étage a une pente de 0 à partir de la valeur minimale jusqu’à 2 207. Après 2 207, la pente de BF27 s’applique, ce qui donne une pente de 361,254. Cette pente persiste jusqu’à ce que le prédicteur atteigne la constante dans BF21, auquel cas les coefficients de BF27 et BF21 affectent prix de vente. La somme des deux coefficients donne la nouvelle pente, 361,254 + (−576,789) = −215,535. Dans un modèle additif, Régression MARS® affiche un diagramme de dépendance partielle à un prédicteur pour montrer l’effet du prédicteur.
Equation de régression
BF3 = lorsque qualité est 8; 9; 10
BF6 = max(0, 2002 - année construite)
BF7 = lorsque sous-sol zone 1 n'est pas manquant
BF10 = max(0, 1696 - sous-sol zone 1) * BF7
BF11 = lorsque qualité est 1; 8
BF13 = lorsque type est 90; 150; 160; 180; 190
BF15 = lorsque quartier est Bluestem; Clear Creek; Collines vertes; Crawford; Northridge;
Northridge Heights; Point de repère; Pont de pierre; Timberland; Veenker; Villages Somerset
BF17 = lorsque superficie totale du sous-sol n'est pas manquant
BF19 = max(0, superficie totale du sous-sol - 1392) * BF17
BF21 = max(0, 1er étage - 2402)
BF23 = lorsque condition est 1; 2; 3; 4; 5; 6
BF25 = lorsque qualité est 1; 7; 10
BF27 = max(0, 1er étage - 2207)
BF30 = max(0, 15138 - zone de lot)
prix de vente = 325577 - 57,6167 * BF2 + 115438 * BF3 - 605,079 * BF6 - 25,3989 * BF10 -
66735,2 * BF11 - 23688,9 * BF13 + 22374,5 * BF15 + 50,3801 * BF19 - 576,789 * BF21 - 18099,2
* BF23 + 22414,2 * BF25 + 361,254 * BF27 - 1,82 * BF30
Fonctions de base pour les valeurs manquantes
Dans la recherche des fonctions de base, Régression MARS® crée des variables d’indicateur pour tous les prédicteurs avec des valeurs manquantes. La variable indicateur indique si une valeur du prédicteur est manquante. Si l’analyse inclut une fonction de base pour un prédicteur avec des valeurs manquantes dans le modèle, le modèle inclut également une fonction de base pour la variable indicateur. Les autres fonctions de base du prédicteur interagissent toutes avec la fonction de base de la variable indicateur.
Lorsqu’un prédicteur a une valeur manquante, la fonction de base de la variable indicateur annule les autres fonctions de base de ce prédicteur par multiplication par 0. Ces fonctions de base pour les valeurs manquantes se trouvent dans tous les modèles où des prédicteurs importants ont des valeurs manquantes, même les modèles additifs et les modèles qui désactivent d’autres types de transformations.
Dans ces résultats, BF7 est pour le prédicteur sous-sol zone 1. BF 7 a une valeur de 1 lorsque sous-sol zone 1 est dans les données. BF 7 a une valeur de 0 lorsqu’il sous-sol zone 1 est manquant. BF7 n’est pas présent dans l’équation de régression parce que la fonction de base n’était pas importante dans le modèle final, mais BF7 interagit avec BF10. BF10 est important et est présent dans l’équation de régression. L’effet de BF7 est de multiplier BF10 par 0 lorsqu’il manque, ce qui supprime l’effet lorsqu’il sous-sol zone 1sous-sol zone 1 manque.
Equation de régression
BF3 = lorsque qualité est 8; 9; 10
BF6 = max(0, 2002 - année construite)
BF7 = lorsque sous-sol zone 1 n'est pas manquant
BF10 = max(0, 1696 - sous-sol zone 1) * BF7
BF11 = lorsque qualité est 1; 8
BF13 = lorsque type est 90; 150; 160; 180; 190
BF15 = lorsque quartier est Bluestem; Clear Creek; Collines vertes; Crawford; Northridge;
Northridge Heights; Point de repère; Pont de pierre; Timberland; Veenker; Villages Somerset
BF17 = lorsque superficie totale du sous-sol n'est pas manquant
BF19 = max(0, superficie totale du sous-sol - 1392) * BF17
BF21 = max(0, 1er étage - 2402)
BF23 = lorsque condition est 1; 2; 3; 4; 5; 6
BF25 = lorsque qualité est 1; 7; 10
BF27 = max(0, 1er étage - 2207)
BF30 = max(0, 15138 - zone de lot)
prix de vente = 325577 - 57,6167 * BF2 + 115438 * BF3 - 605,079 * BF6 - 25,3989 * BF10 -
66735,2 * BF11 - 23688,9 * BF13 + 22374,5 * BF15 + 50,3801 * BF19 - 576,789 * BF21 - 18099,2
* BF23 + 22414,2 * BF25 + 361,254 * BF27 - 1,82 * BF30
Fonctions de base pour les interactions
Pour modéliser les interactions, Régression MARS® multiplie les fonctions de base pour différents prédicteurs. Régression MARS® Ne prend pas en compte les interactions dans le modèle additif par défaut. Les diagrammes de dépendance partielle ne sont pas disponibles pour une analyse qui tient compte des interactions.
Une interaction signifie que l’effet d’un prédicteur dépend de la valeur d’autres prédicteurs. Par exemple, la vitesse à laquelle le grain sèche dans un four dépend du temps passé dans le four, mais l’effet du temps dépend de la température du four. Les variables de temps et de température interagissent.
Dans les résultats d’un modèle avec interactions, BF9 est pour le prédicteur qualité. BF12 est pour le prédicteur 1er étage. Le calcul de BF12 inclut la multiplication par BF9, de sorte que les deux prédicteurs interagissent. Détermination de l’effet de ou qualité nécessite la connaissance de la valeur de 1er étage l’autre prédicteur. Le coefficient pour BF12 de −63,1685 ne s’applique que lorsque la valeur de BF9 est 1. La valeur de BF9 est 1 lorsque qualité est 8, 9 ou 10. En raison de la disposition de BF12, 1er étage a une pente de 63,1685 lorsque la superficie est inférieure à 2 470 et la valeur de qualité est 8, 9 ou 10.
Equation de régression
BF4 = max(0, 2002 - année construite)
BF5 = lorsque sous-sol zone 1 n'est pas manquant
BF7 = max(0, sous-sol zone 1 - 1758) * BF5
BF8 = max(0, 1758 - sous-sol zone 1) * BF5
BF9 = lorsque qualité est 8; 9; 10
BF12 = max(0, 2470 - 1er étage) * BF9
BF14 = lorsque qualité est 7; 9; 10
BF15 = lorsque type est 75; 90; 150; 160; 180; 190
BF19 = lorsque quartier est Bluestem; Clear Creek; Collines vertes; Crawford; Northridge;
Northridge Heights; Pont de pierre; Timberland; Veenker; Verts; Villages Somerset * BF5
BF21 = lorsque condition est 1; 2; 3; 4; 5; 6 * BF4
BF25 = max(0, 1er étage - 372) * BF7
BF26 = lorsque superficie totale du sous-sol n'est pas manquant * BF14
BF28 = max(0, superficie totale du sous-sol - 689) * BF26
prix de vente = 320349 - 66,4387 * BF2 - 28,2065 * BF8 + 123645 * BF9 - 63,1685 * BF12 -
23751,7 * BF15 + 22818,2 * BF19 - 523,924 * BF21 - 0,036887 * BF25 + 53,9878 * BF28
