Remarque
Cette commande est disponible avec le Module d'analyse prédictive. Cliquez ici pour plus d'informations sur l'activation du module.
Une équipe de chercheurs recueille des données sur la vente de propriétés résidentielles individuelles à Ames, iowa. Les chercheurs veulent identifier les variables qui influent sur le prix de vente. Les variables incluent la surface du terrain et diverses caractéristiques de la propriété résidentielle. Les chercheurs veulent évaluer dans quelle mesure le meilleur modèle MARS® correspond aux données.
- Ouvrez les données échantillons, Ames_logement.MWX.
- Sélectionnez .
- Dans la zone Réponse, saisissez ‘prix de vente’.
- Dans Prédicteurs continus, entrez ‘façade de lot' – ‘année vendue’.
- Dans Prédicteurs de catégorie, entrez type – 'condition de vente’.
- Cliquez sur OK.
Interpréter des résultats
Par défaut, Régression MARS® s’adapte à un modèle additif de sorte que toutes les fonctions de base de l’équation de régression utilisent 1 prédicteur. Le premier prédicteur de la liste est BF2. BF2 utilise le prédicteur zone de vie. Parce que le prédicteur est dans 1 fonction de base, le prédicteur a 2 pentes différentes dans le modèle. La fonction max(0, 3078 - zone de vie) définit que la pente est différente de zéro lorsque la surface habitable est inférieure à 3 078.
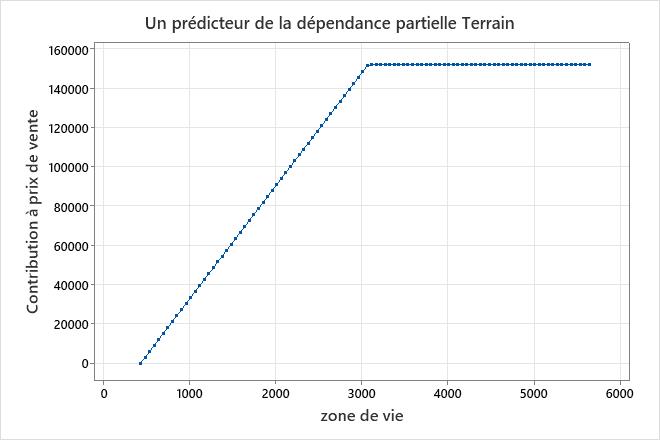
Les résultats d’un modèle additif comprennent des diagrammes de dépendance partielle pour les prédicteurs continus qui sont importants dans le modèle. Utilisez le graphique pour voir l’effet de toutes les fonctions de base d’un prédicteur sur toute la plage du prédicteur. Dans ces résultats, le diagramme de dépendance partielle montre que pour une valeur de zone de vie 438 à 3 078, la pente est d’environ 57,6. Lorsque zone de vie est supérieur à 3 078, la pente est égale à 0.
Dans ces résultats, BF2 a un coefficient négatif dans l’équation de régression. La disposition de la fonction de base est max(0, c - X). Dans cet arrangement, la valeur de la fonction de base diminue lorsque le prédicteur augmente. La combinaison de cet arrangement et du coefficient négatif crée une relation positive entre la variable prédictive et la variable de réponse. L’effet de est d’augmenter prix de vente dans la région de zone de vie 438 à 3 078.
L’analyse comprend également des prédicteurs catégoriels. Par exemple, BF3 est pour le prédicteur qualité. La fonction de base est pour lorsque la valeur de qualité est 8, 9 ou 10. Le coefficient BF3 dans l’équation est 115 438. Cette fonction de base indique que lorsque la valeur de la qualité passe d’une valeur de 1 à 7 à une valeur de 8, 9 ou 10, le prix de vente augmente de 115 438 $ dans le modèle. qualité est également dans BF11 et BF25. Pour comprendre l’effet du prédicteur sur la variable de réponse, considérez toutes les fonctions de base.
Deux des prédicteurs importants dans le modèle ont des valeurs manquantes dans les données d’apprentissage : sous-sol zone 1 et superficie totale du sous-sol. La liste des fonctions de base comprend des fonctions de base qui identifient quand ces prédicteurs sont manquants : BF7 et BF17. Lorsqu’un prédicteur ou une valeur manquante, la fonction de base de la variable indicateur annule les autres fonctions de base de ce prédicteur par multiplication par 0.
Equation de régression
BF3 = lorsque qualité est 8; 9; 10
BF6 = max(0, 2002 - année construite)
BF7 = lorsque sous-sol zone 1 n'est pas manquant
BF10 = max(0, 1696 - sous-sol zone 1) * BF7
BF11 = lorsque qualité est 1; 8
BF13 = lorsque type est 90; 150; 160; 180; 190
BF15 = lorsque quartier est Bluestem; Clear Creek; Collines vertes; Crawford; Northridge;
Northridge Heights; Point de repère; Pont de pierre; Timberland; Veenker; Villages Somerset
BF17 = lorsque superficie totale du sous-sol n'est pas manquant
BF19 = max(0, superficie totale du sous-sol - 1392) * BF17
BF21 = max(0, 1er étage - 2402)
BF23 = lorsque condition est 1; 2; 3; 4; 5; 6
BF25 = lorsque qualité est 1; 7; 10
BF27 = max(0, 1er étage - 2207)
BF30 = max(0, 15138 - zone de lot)
prix de vente = 325577 - 57,6167 * BF2 + 115438 * BF3 - 605,079 * BF6 - 25,3989 * BF10 -
66735,2 * BF11 - 23688,9 * BF13 + 22374,5 * BF15 + 50,3801 * BF19 - 576,789 * BF21 - 18099,2
* BF23 + 22414,2 * BF25 + 361,254 * BF27 - 1,82 * BF30
Remarque
Dans ces résultats, la liste des fonctions de base comporte 15 fonctions de base, mais le nombre optimal de fonctions de base est de 13. L’équation de régression contient 13 fonctions de base. La liste des fonctions de base contient BF7 et BF17, qui sont les fonctions de base qui identifient les valeurs manquantes. Ces fonctions de base ne sont pas importantes en elles-mêmes parce qu’elles n’ont pas réduit le MSE autant que les autres fonctions de base dans la recherche. Ces 2 fonctions de base sont dans la liste pour montrer le calcul complet de BF10 et BF 19, qui sont importantes.
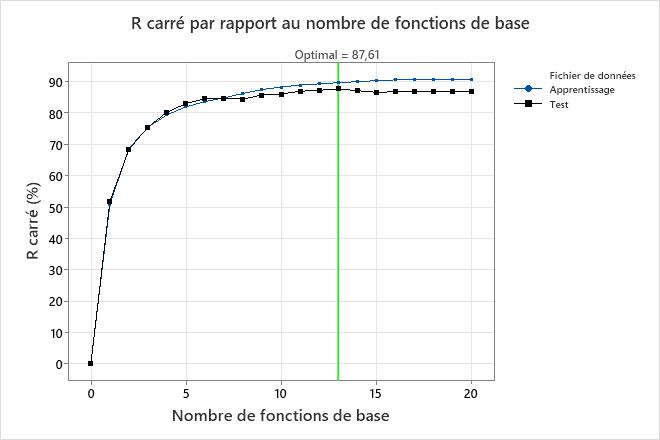
Le graphique R-carré vs Nombre de fonctions de base montre le résultat de l’élimination vers l’arrière pour trouver le nombre optimal de fonctions de base. Pour utiliser un modèle avec un nombre différent de fonctions de base, sélectionnez Sélectionner un autre modèle. Par exemple, si un modèle avec beaucoup moins de fonctions de base est presque aussi précis que le modèle optimal, déterminez s’il faut utiliser le modèle le plus simple. Dans ces résultats, les valeurs R-carré pour les ensembles de données d’apprentissage et de test sont les mêmes pour le modèle avec 7 fonctions de base. Ce modèle plus petit est intéressant si le surajustement est une préoccupation.
Récapitulatif du modèle
| Nombre total de prédicteurs | 77 |
|---|---|
| Prédicteurs importants | 10 |
| Nombre maximal de fonctions de base | 30 |
| Nombre optimal de fonctions de base | 13 |
| Statistiques | Apprentissage | Test |
|---|---|---|
| R carré | 89,61% | 87,61% |
| Racine de l'erreur quadratique moyenne (RMSE) | 25836,5197 | 27855,6550 |
| Erreur quadratique moyenne (MSE) | 667525749,7185 | 775937512,8264 |
| Ecart absolu moyen (MAD) | 17506,0038 | 17783,5549 |
Le tableau récapitulatif du modèle comprend des mesures de la performance du modèle. Vous pouvez utiliser ces valeurs pour comparer des modèles. Pour ces résultats, le test R-carré est d’environ 88%.
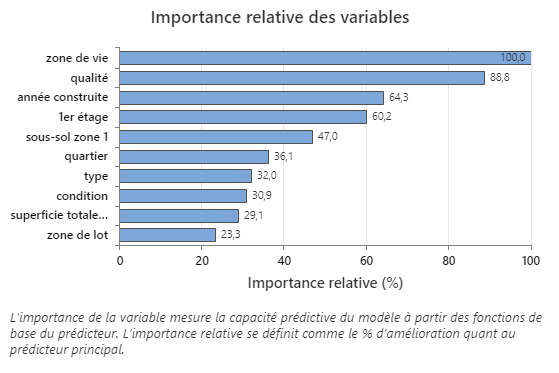
Le graphique d’importance relative des variables représente les prédicteurs dans l’ordre de leur effet sur le modèle. La variable de prédiction la plus importante est zone de vie. Si la contribution de la variable prédictive supérieure, zone de vie, est de 100 %, alors la variable importante suivante, qualité, a une contribution de 44,4 %. Cette contribution signifie que c’est 88,8% aussi important que qualitézone de vie dans ce modèle.
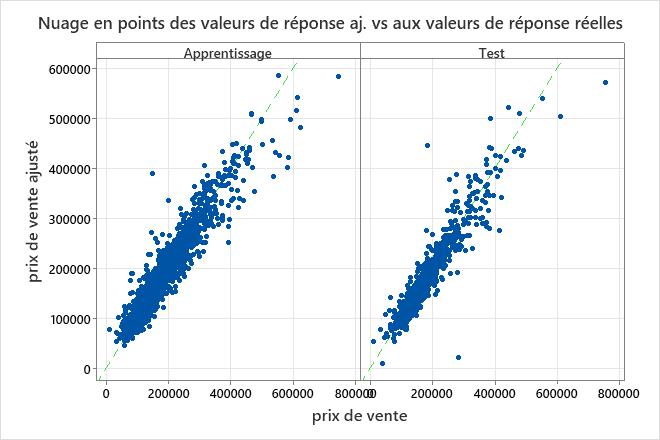
Le nuage de points entre les prix de vente ajustés et les prix de vente réels montre la relation entre les valeurs ajustées et réelles pour les données d’entraînement et les données d’essai. Pour identifier plus facilement les valeurs représentées, survolez les points du graphique. Dans cet exemple, la plupart des points se situent approximativement près de la ligne de référence y=x.
Le modèle correspond mal à quelques points distincts, comme celui de l’ensemble de données de test qui a un prix de vente ajusté inférieur à 100 000 $ mais un prix de vente réel plus proche de 250 000 $. Déterminez s’il faut enquêter sur ce cas pour améliorer l’ajustement du modèle.
