Sur ce thème
Etape 1 : Etudier les arbres alternatifs
Le diagramme du R carré par rapport au nombre de nœuds terminaux affiche la valeur de R2 pour chaque arbre. Par défaut, l'arbre de régression initial est le plus petit arbre avec une valeur de R2située à moins d'1 erreur type de la valeur correspondant à l'arbre avec la valeur de R2 maximale. Lorsque l'analyse utilise une validation croisée ou un ensemble de données de test, la valeur de R2 provient de l'échantillon de validation. Les valeurs de l'échantillon de validation se stabilisent généralement et finissent par diminuer à mesure que l'arbre grandit.
Cliquez sur Sélectionner un arbre alternatif pour ouvrir un diagramme interactif qui comprend un tableau de statistiques récapitulatives du modèle. Utilisez le diagramme pour étudier les arbres alternatifs ayant des performances similaires.
- L'arbre choisi par Minitab fait partie d'un schéma dans lequel le critère s'améliore. Un ou plusieurs arbres ayant quelques nœuds de plus font partie du même modèle. Généralement, lorsque vous faites des prévisions à partir d'un arbre, il est préférable de bénéficier de la plus grande exactitude possible.
- L'arbre choisi par Minitab fait partie d'un schéma dans lequel le critère est relativement stable. Un ou plusieurs arbres présentant des statistiques récapitulatives similaires pour le modèle ont beaucoup moins de nœuds que l'arbre optimal. Généralement, un arbre avec moins de nœuds terminaux donne une idée plus claire de l'effet de chaque variable de prévision sur les valeurs de réponse. Un arbre plus petit facilite également l'identification de quelques groupes cibles pour effectuer d'autres études. Si la différence dans l'exactitude de prévision pour un arbre plus petit est négligeable, vous pouvez également utiliser le plus petit arbre pour évaluer les relations entre les variables de réponse et de prévision.
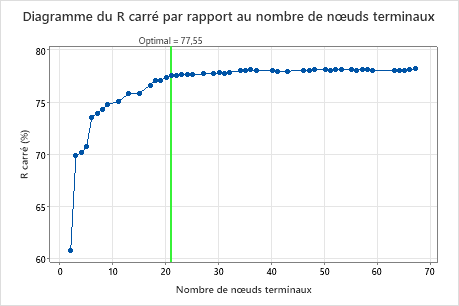
Principal résultat : Diagramme du R carré par rapport au nombre de nœuds terminaux pour un arbre avec 21 nœuds terminaux
L'arbre de régression avec 21 nœuds terminaux a une valeur de R2 d'environ 0,78. Cet arbre porte l'étiquette "Optimal" car le critère de création de l'arbre était le plus petit arbre présentant une valeur de R2 située à moins d'1 erreur type de la valeur de R2 maximale. Comme ce graphique montre que les valeurs de R2 sont relativement stables entre les arbres ayant environ 20 nœuds et ceux ayant environ 70 nœuds, les chercheurs veulent examiner les performances de certains arbres encore plus petits qui sont similaires à l'arbre dans les résultats. Comparez le graphique suivant pour voir les résultats d'un arbre avec 17 nœuds.
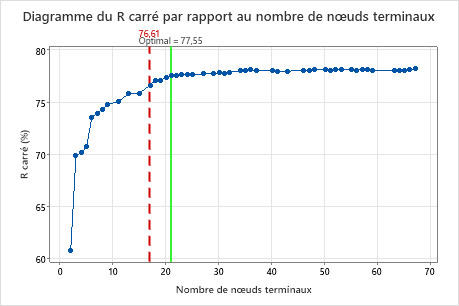
Principal résultat : Diagramme du R carré par rapport au nombre de nœuds terminaux pour un arbre avec 17 nœuds terminaux
L'arbre de régression avec 17 nœuds terminaux a une valeur de R2 de 0,7661. L'arbre des résultats initiaux conserve l'étiquette "Optimal" lorsque vous utilisez Sélectionner un arbre alternatif pour créer des résultats pour un arbre différent.
Etape 2 : Etudier les nœuds intéressants sur l'arborescence
Après avoir sélectionné un arbre, étudiez les nœuds terminaux distinctifs sur l'arborescence. Par exemple, vous pourriez être intéressé par les nœuds avec de grandes moyennes ou avec de petits écarts types. Depuis la vue détaillée, vous pouvez voir la moyenne, l'écart type et les dénombrements totaux pour chaque nœud.
Remarque
Cliquez sur l'arborescence avec le bouton droit de la souris pour effectuer les interactions suivantes :
- Mettre en surbrillance les 5 nœuds présentant le moins de variation par rapport à la valeur ajustée pour le nœud. Ces nœuds sont les nœuds optimaux.
- Mettre en surbrillance les 5 nœuds ayant les moyennes ou les médianes les plus élevées, en fonction du critère de l'arbre.
- Mettre en surbrillance les 5 nœuds avec les moyennes ou les médianes les plus faibles, en fonction du critère de l'arbre.
- Copier les valeurs des prédicteurs qui mènent à un nœud que vous sélectionnez. Ces valeurs sont les règles du nœud.
- Afficher la vue de division de nœud. Cette vue est utile lorsque vous avez un grand arbre et que vous voulez uniquement voir quelles variables divisent les nœuds.
Les nœuds continuent de se diviser jusqu'à ce que les nœuds terminaux ne puissent plus être divisés en groupements supplémentaires. Explorez d'autres nœuds pour voir quelles variables sont les plus intéressantes.
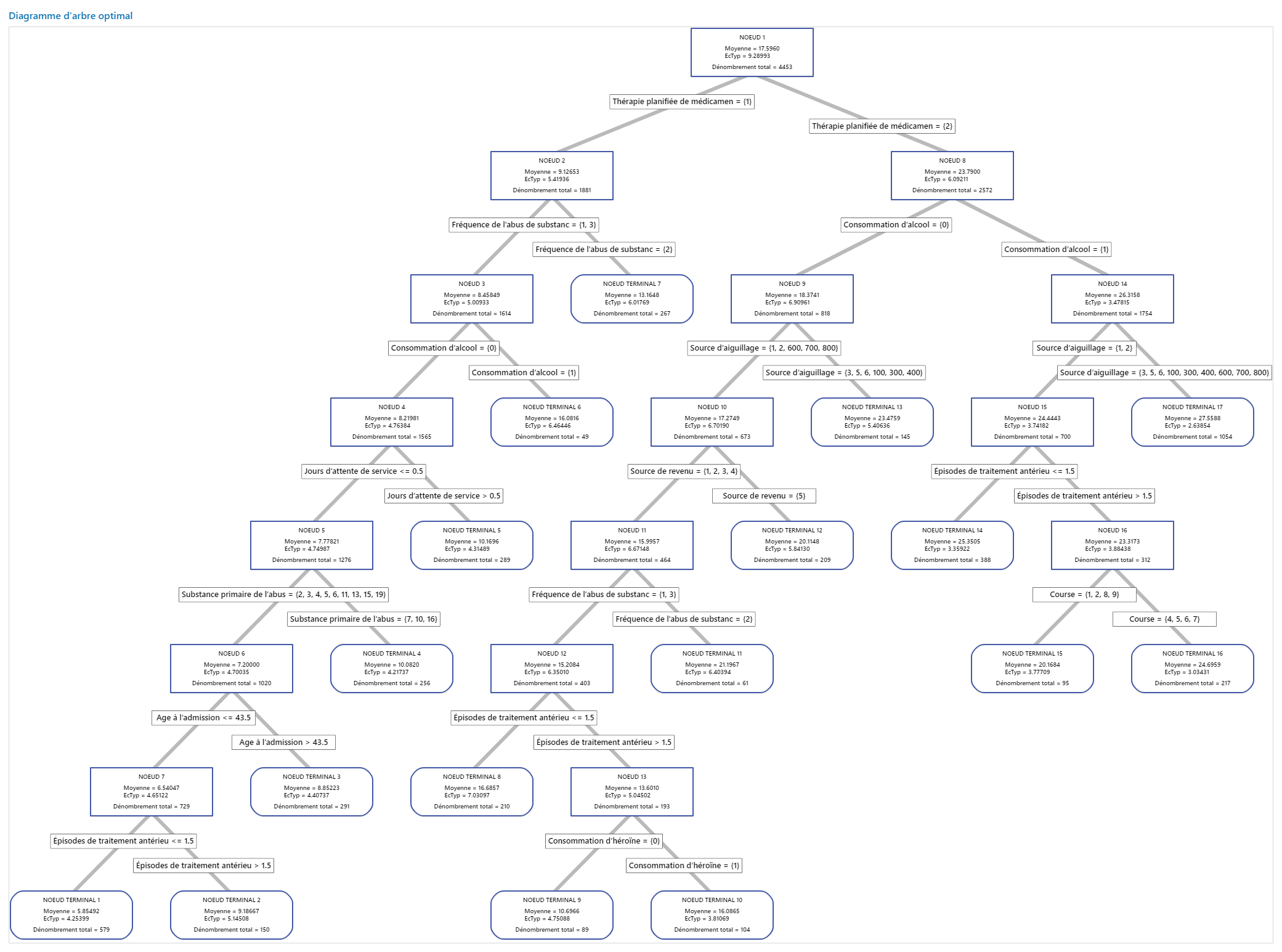
Principal résultat : Arborescence pour l'arbre à 17 nœuds
L'arborescence montre les 4 453 cas de l'ensemble complet de données. Vous pouvez basculer entre la vue détaillée et la vue de partition de nœud de l'arbre.
- Le Nœud 2 comprend les cas où Thérapie planifiée de médicaments = 1. Ce nœud compte 1 881 cas. La moyenne pour le nœud est inférieure à la moyenne globale. L'écart type pour le Nœud 2 est d'environ 5,4, ce qui est inférieur à l'écart type global car une partition donne des nœuds plus purs.
- Le Nœud 8 comprend les cas où Thérapie planifiée de médicaments = 2. Ce nœud compte 2 572 cas. La moyenne pour le nœud est supérieure à la moyenne globale. L'écart type pour le Nœud 8 est d'environ 6,1, ce qui est également inférieur à l'écart type global.
Ensuite, le Nœud 2 est divisé par Fréquence de l’abus de substances et le Nœud 8 est divisé par Consommation d’alcool. Le Nœud terminal 17 comprend les cas où Thérapie planifiée de médicaments = 2, Consommation d’alcool = 1 et Source d’aiguillage = 3, 5, 6, 100, 300, 400, 600, 700 ou 800. Les chercheurs notent que le Nœud terminal 17 a la moyenne la plus élevée, le plus petit écart type et la plupart des cas.
Le Nœud terminal 1 a la plus petite moyenne et un écart type d'environ 4,3. Etant donné que la moyenne du Nœud terminal 1 est d'environ 5,9 et que les valeurs de réponse ne peuvent pas être négatives, les statistiques sur les nœuds suggèrent que les données du Nœud terminal 1 sont probablement asymétriques vers la droite.
Etape 3 : Déterminer les variables importantes
Utilisez la courbe d'importance relative des variables pour déterminer quels prédicteurs sont les variables les plus importantes pour l'arbre.
Les variables importantes constituent un séparateur principal ou de substitution dans l'arbre. La variable avec le score d'amélioration le plus élevé est la variable la plus importante, et les autres variables sont classées en conséquence. L'importance relative des variables normalise les valeurs d'importance pour faciliter l'interprétation. L'importance relative se définit comme l'amélioration en pourcentage par rapport au prédicteur le plus important.
Les valeurs d'importance relative des variables varient de 0 % à 100 %. La variable la plus importante a toujours une importance relative de 100 %. Si une variable n'est pas dans l'arbre, cette variable n'est pas importante.
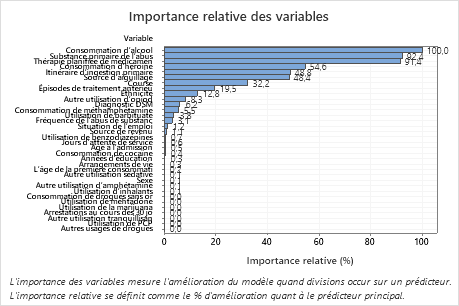
Principal résultat : Importance relative des variables
- Substance primaire de l’abus et Thérapie planifiée de médicaments sont environ 92 % aussi importantes que Consommation d’alcool.
- Consommation d’héroïne est environ 55 % aussi importante que Consommation d’alcool.
- Itinéraire d’ingestion primaire de Sous-Marin et Source d’aiguillage sont environ 48 % aussi importantes que Consommation d’alcool.
Bien que ces résultats comprennent 33 variables ayant une importance positive, les classements relatifs fournissent des informations sur le nombre de variables à contrôler ou à surveiller pour une certaine application. Les baisses abruptes des valeurs d'importance relative d'une variable à la variable suivante peuvent guider les décisions sur les variables à contrôler ou à surveiller. Par exemple, dans ces données, les trois variables les plus importantes ont des valeurs d'importance qui sont relativement proches les unes des autres avant une baisse de près de 40 % par rapport à la variable suivante. De même, trois variables ont des valeurs d'importance similaires de près de 50 %. Vous pouvez supprimer les variables de différents groupes et refaire l'analyse pour évaluer l'impact des variables de différents groupes sur les valeurs d'exactitude de prévision dans le tableau récapitulatif du modèle.
