Un prestataire de soins de santé gère un établissement qui offre des services de traitement de la toxicomanie. L'un des services de l'établissement est un programme de désintoxication en ambulatoire où un traitement courant peut durer de 1 à 30 jours. Une équipe chargée de prévoir le personnel et les fournitures nécessaires veut savoir si elle peut améliorer la qualité de ses prévisions de la durée d'utilisation des services par les patients en se fondant sur les informations qu'elle peut recueillir sur le patient lorsque celui-ci intègre le programme. Ces variables comprennent des informations démographiques et des variables sur l'addiction du patient.
Tout d'abord, l'équipe effectue une analyse de régression traditionnelle dans Minitab. En raison du modèle de valeur manquant dans leurs données, l’analyse omet plus de 70% des données. L'omission d'un si grand pourcentage de données implique que beaucoup d'informations sont perdues. Les résultats analytiques des cas sans aucune donnée manquante peuvent être très différents des résultats utilisant l'ensemble complet de données. Comme Régression CART® gère automatiquement les valeurs manquantes dans les variables de prévision, l'équipe décide d'utiliser Régression CART® pour évaluer plus avant leurs données.
- Ouvrez l'ensemble de données échantillons DureeDuService.MWX.
- Sélectionnez .
- Dans Réponse, saisissez 'Durée du service'.
- Dans Prédicteurs continus, saisissez 'Age à l’admission'-'Années d’éducation'.
- Dans Prédicteurs de catégorie, saisissez 'Autre utilisation de stimulants'-'Diagnostic DSM'.
- Cliquez sur Validation.
- Dans Méthode de validation, sélectionnez Validation croisée sur K ensembles.
- Sélectionnez Affecter des lignes de chaque partition par colonne d'ID.
- Dans Colonne d'ID, saisissez Plier.
- Cliquez sur OK dans chaque boîte de dialogue
Interpréter des résultats
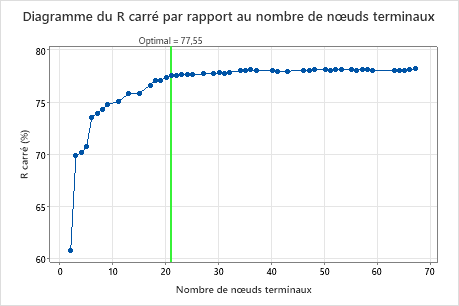
Par défaut, Minitab affiche le plus petit arbre avec une valeur de R2 située à moins d'1 erreur type de l'arbre ayant la valeur de R2 maximale. Étant donné que l'équipe de soins de santé utilise la validation sur K partitions, le critère est la valeur maximale de R2 sur K partitions. Cet arbre comprend 21 nœuds terminaux.
Sélectionner un arbre alternatif
- Dans la sortie, cliquez sur Sélectionner un arbre alternatif.
- Dans le diagramme, sélectionnez l'arbre à 17 nœuds.
- Cliquez sur Créer un arbre.
Interpréter des résultats
Les chercheurs consultent le diagramme de la statistique R2 issue de la validation croisée avec le nombre de nœuds terminaux. Comme l'arbre à 17 nœuds comprend une statistique R2 proche des plus grandes valeurs du diagramme, les résultats du reste de la sortie sont pour l'arbre à 17 nœuds.
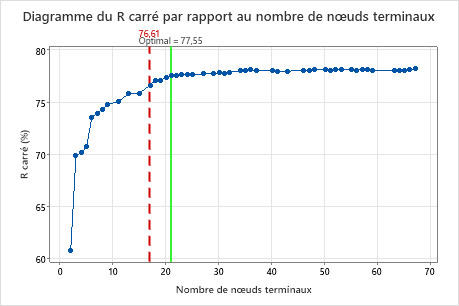
Les chercheurs consultent d'abord le récapitulatif du modèle pour évaluer les performances du plus petit arbre. Les valeurs pour les statistiques d'apprentissage et de test sont proches les unes des autres. Par conséquent, l'arbre ne semble pas surajusté. La statistique R2 est presque aussi élevée que pour l'arbre à 21 nœuds. Les chercheurs décident donc d'utiliser l'arbre à 17 nœuds pour explorer les relations entre les variables de prévision et les valeurs de réponse.
Méthode
| Division des nœuds | Erreur des moindres carrés |
|---|---|
| Arbre optimal | Dans 2,5 erreur(s) type(s) du R carré maximum |
| Validation de modèle | Validation croisée avec lignes définies par Plier |
| Lignes utilisées | 4453 |
Informations de réponse
| Moyenne | EcTyp | Minimum | Q1 | Médiane | Q3 | Maximum |
|---|---|---|---|---|---|---|
| 17,5960 | 9,29097 | 1 | 10 | 18 | 26 | 30 |
Récapitulatif du modèle
| Nombre total de prédicteurs | 44 |
|---|---|
| Prédicteurs importants | 33 |
| Nombre de nœuds terminaux | 17 |
| Taille minimale du nœud terminal | 49 |
| Statistiques | Apprentissage | Test |
|---|---|---|
| R carré | 77,99% | 76,61% |
| Racine de l'erreur quadratique moyenne (RMSE) | 4,3585 | 4,4932 |
| Erreur quadratique moyenne (MSE) | 18,9967 | 20,1887 |
| Ecart absolu moyen (MAD) | 3,4070 | 3,5226 |
| Pourcentage d'erreur absolue moyen (MAPE) | 0,6535 | 0,6674 |
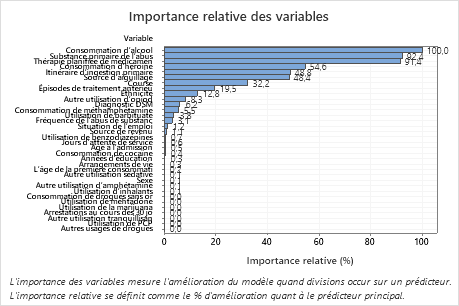
- 'Substance primaire de l’abus' et 'Thérapie planifiée de médicaments' sont environ 92% aussi importants que 'Consommation d’alcool'.
- 'Consommation d’héroïne' est environ 55% aussi important que 'Consommation d’alcool'.
- 'Itinéraire d’ingestion primaire de Sous-Marin' et 'Source d’aiguillage' sont environ 48% aussi importants que 'Consommation d’alcool'.
Bien que ces résultats comprennent 33 variables d'importance positive, les classements relatifs fournissent des informations sur le nombre de variables à contrôler ou à surveiller pour une certaine application. Les baisses abruptes des valeurs d'importance relative d'une variable à la suivante peuvent guider les décisions sur les variables à contrôler ou à surveiller. Par exemple, dans ces données, les trois variables les plus importantes ont des valeurs d'importance relativement proches les unes des autres avant une baisse de près de 40 % pour la variable suivante. De même, trois variables ont des valeurs d’importance similaires proches de 50 %. Vous pouvez supprimer les variables de différents groupes et refaire l'analyse pour évaluer l'effet des variables de différents groupes sur les valeurs d'exactitude de prévision dans le tableau récapitulatif du modèle.
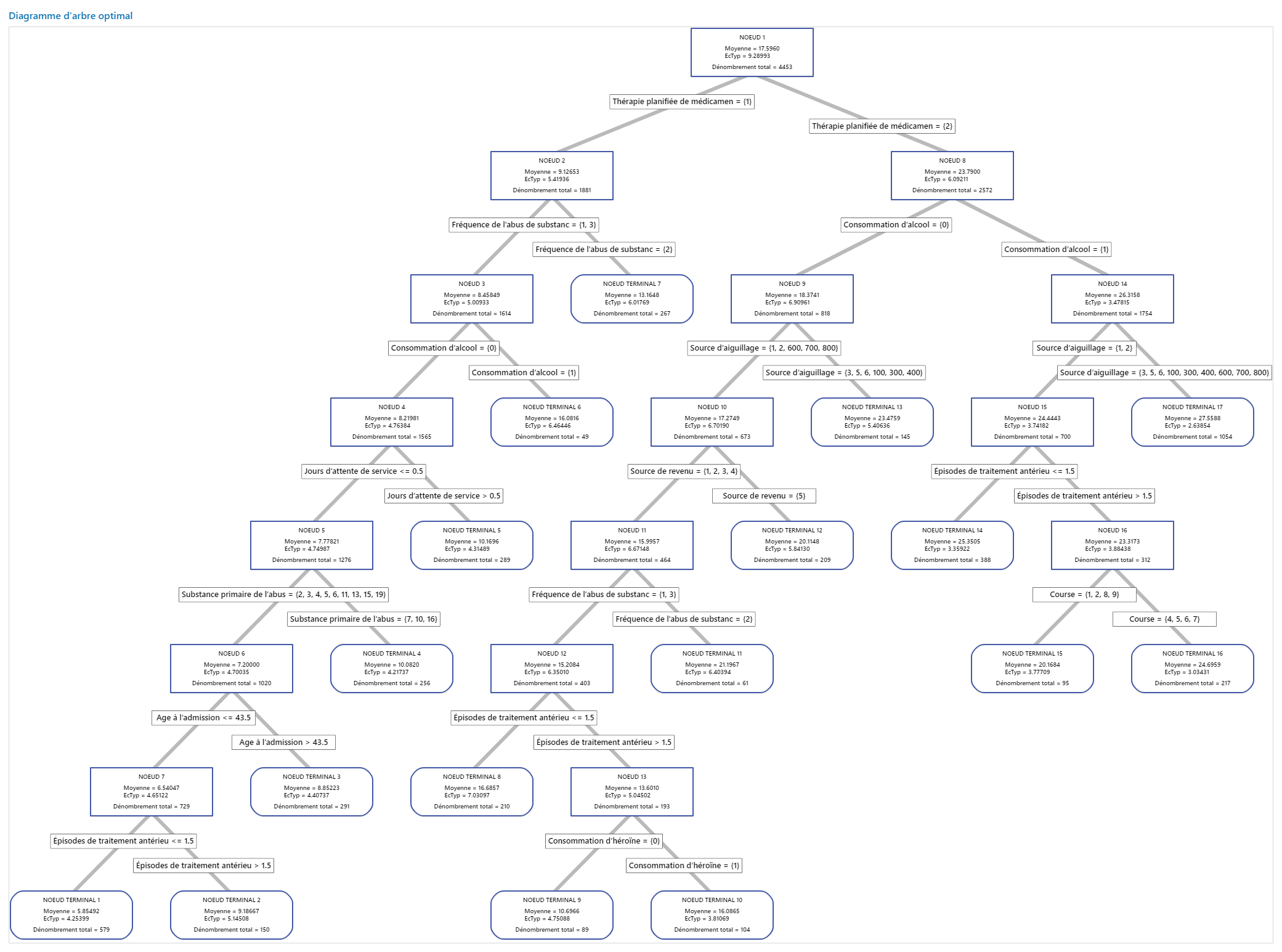
Pour une analyse avec une validation croisée sur K partitions, l'arborescence montre les 4 453 cas de l'ensemble complet de données. Vous pouvez basculer entre la vue détaillée et la vue de partition de nœud de l'arbre. Le tableau des valeurs ajustées et des statistiques d'erreur, et les critères de classification des sujets donnent des informations supplémentaires sur les nœuds terminaux.
- Le Nœud 2 comprend les cas où 'Thérapie planifiée de médicaments' = 1. Ce nœud compte 1 881 cas. La moyenne pour le nœud est inférieure à la moyenne globale. L'écart type pour le Nœud 2 est d'environ 5,4, ce qui est inférieur à l'écart type global car une partition donne des nœuds plus purs.
- Le Nœud 8 comprend les cas où 'Thérapie planifiée de médicaments' = 2. Ce nœud compte 2572 cas. La moyenne pour le nœud est supérieure à la moyenne globale. L'écart type pour le Nœud 8 est d'environ 6,1, ce qui est également inférieur à l'écart type global.
Ensuite, le Nœud 2 est divisé par 'Fréquence de l’abus de substances' et le Nœud 8 est divisé par 'Consommation d’alcool'. Le Nœud terminal 17 comprend les cas où 'Thérapie planifiée de médicaments' = 2, 'Consommation d’alcool' = 1 et 'Source d’aiguillage' = 3, 5, 6, 100, 300, 400, 600, 700 ou 800. Les chercheurs notent que le Nœud terminal 17 a la moyenne la plus élevée, le plus petit écart type et le plus grand nombre de cas.
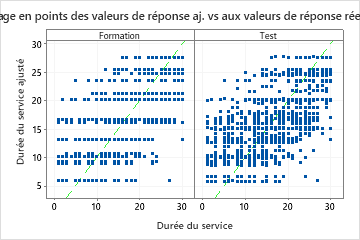
Les résultats comprennent un nuage de points des valeurs de réponse ajustées et des valeurs de réponse réelles. Les points de l'ensemble de données d'apprentissage et de l'ensemble de données de test présentent des schémas similaires. Cette similitude suggère que les performances de l'arbre avec de nouvelles données sont proches de celles obtenues avec les données d'apprentissage.
- 'Thérapie planifiée de médicaments' = {2}
- 'Consommation d’alcool' = {0}
- 'Source d’aiguillage' = {1, 2, 600, 700, 800}
- 'Source de revenu' = {1, 2, 3, 4}
- 'Fréquence de l’abus de substances' = {1, 3}
- 'Épisodes de traitement antérieurs' <= 1,5
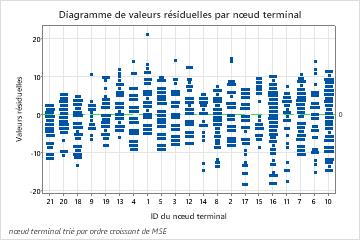
Le diagramme des valeurs résiduelles par nœud terminal montre que la valeur ajustée est trop grande pour un petit groupe de patients dans le Nœud terminal 8. Les analystes envisagent une enquête pour savoir pourquoi certains de ces patients utilisent les services moins longtemps qu'un patient type de leur groupe. Si par exemple ces patients se trouvent dans un lieu géographique différent des autres patients du nœud terminal, des réglementations différentes au niveau des services publics et des polices d'assurance pourraient avoir un effet sur la durée d'utilisation des services.
Le diagramme des valeurs résiduelles par nœud terminal montre d'autres cas pour lesquels les analystes peuvent choisir d'enquêter sur les groupes ou les valeurs aberrantes. Par exemple, dans ces données, une valeur résiduelle semble beaucoup plus grande que les autres dans le Nœud terminal 1 et dans le Nœud terminal 7. Les analystes décident de rechercher pourquoi ces patients ont utilisé les services plus longtemps que d'autres patients dans leur nœud terminal.
Étant donné que la valeur de R2 de test laisse une marge d'amélioration et que les diagrammes des valeurs résiduelles montrent que l'arbre n'offre pas un bon ajustement, les chercheurs examinent s'il convient d'utiliser un Régression TreeNet® ou un Régression Random Forests® pour essayer d'améliorer l'ajustement.