Prédicteurs importants
Tout arbre de classification est une collection de divisions. Chaque division apporte une amélioration à l'arbre. Chaque division comprend également des divisions de substitution qui apportent également une amélioration à l'arbre. L'importance d'une variable est donnée par toutes ses améliorations lorsque l'arbre l'utilise pour diviser un nœud, que ce soit directement ou comme substitut lorsqu'une valeur est manquante pour une autre variable.
La formule suivante donne l'amélioration à un seul nœud :
Les valeurs de I(t), de pGauche et de pDroite dépendent du critère de partition des nœuds. Pour plus d'informations, accédez à Méthodes de partition des nœud dans Classification CART®.
Moyenne du log négatif de vraisemblance
Données d’apprentissage ou aucune validation
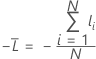
où
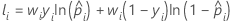
Notation pour les données d’apprentissage ou aucune validation
| Terme | Description |
|---|---|
| N | effectif de l’échantillon des données complètes ou des données d’apprentissage |
| wi | pondération pour la ie observation de l'ensemble de données complet ou de l'ensemble de données d'apprentissage |
| yi | variable d’indicateur qui est de 1 pour l’événement et de 0 autrement dans l’ensemble de données complet ou dans l’ensemble de données d’apprentissage |
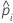 | probabilité prévue de l'événement pour la ie ligne de l'ensemble de données complet ou de l'ensemble de données d'apprentissage |
Validation croisée sur K ensembles
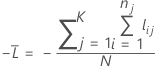
où
Notation pour la validation croisée sur K partitions
| Terme | Description |
|---|---|
| N | effectif de l’échantillon des données complètes ou des données d’apprentissage |
| nj | effectif de l'échantillon de la partition j |
| wij | pondération pour la ie observation dans la partition j |
| yij | variable d'indicateur qui est de 1 pour l'événement et de 0 autrement pour les données de la partition j |
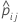 | probabilité prévue de l'événement à partir de l'estimation du modèle qui n'inclut pas les observations pour la ie observation dans la partition j |
Ensemble de données de test
où
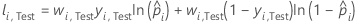
Notation pour l’ensemble de données de test
| Terme | Description |
|---|---|
| nTest | effectif de l’échantillon de l’ensemble de test |
| wi, Test | pondération pour la ie observation dans l'ensemble de données de test |
| yi, Test | variable d’indicateur qui est de 1 pour l’événement et de 0 autrement pour les données de l’ensemble de test |
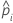 | probabilité prévue de l'événement pour la ie ligne dans l'ensemble de test |
Aire sous la courbe ROC
Formule
Minitab utilise une intégration pour l'aire sous la courbe.
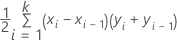
où k est le nombre de nœuds terminaux et (x0, y0) est le point (0, 0).
| X (taux de faux positifs) | Y (taux de vrais positifs) |
|---|---|
| 0,0923 | 0,3051 |
| 0,4154 | 0,7288 |
| 0,7538 | 0,9322 |
| 1 | 1 |
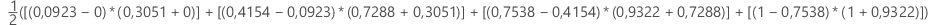
Notation
| Terme | Description |
|---|---|
| TRP | taux de vrais positifs |
| FPR | taux de faux positifs |
| TP | vrais positifs, événements qui ont été correctement évalués |
| P | nombre d’événements positifs réels |
| FP | vrais négatifs, non-événements qui ont été correctement évalués |
| N | nombre d’événements négatifs réels |
| FNR | taux de faux négatifs |
| TNR | taux de vrais négatifs |
IC à 95 % pour l'aire sous la courbe ROC
L’intervalle suivant donne les limites supérieure et inférieure de l’intervalle de confiance :
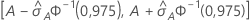
Le calcul de l'erreur type de l'aire sous la courbe ROC (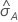
) provient de Salford Predictive Modeler®. Pour obtenir des informations générales sur l’estimation de la variance de l'aire située sous la courbe ROC, consultez les références suivantes :
Engelmann, B. (2011). Measures of a ratings discriminative power: Applications and limitations, Dans B. Engelmann et R. Rauhmeier (Eds.), The Basel II Risk Parameters:Estimation, Validation, Stress Testing - With Applications to Loan Risk Management (2e éd.) Heidelberg ; New York : Springer. doi :10.1007/978-3-642-16114-8
Cortes, C. et Mohri, M. (2005). Confidence intervals for the area under the ROC curve. Advances in neural information processing systems, 305-312.
Feng, D., Cortese, G. et Baumgartner, R. (2017). A comparison of confidence/credible interval methods for the area under the ROC curve for continuous diagnostic tests with small sample size. Statistical Methods in Medical Research, 26(6), 2603-2621. doi :10.1177/0962280215602040
Notation
| Terme | Description |
|---|---|
| A | aire située sous la courbe ROC |
 | 0,975 percentile de la loi normale standard |
Lift
Formule
Pour les 10 % d’observations des données ayant les probabilités les plus élevées d’être affectées à la classe d’événement, utilisez la formule suivante.
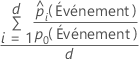
Pour le lift de test avec un ensemble de données de test, utilisez les observations de l’ensemble de données de test. Pour le lift de test avec la validation croisée sur K partitions, sélectionnez les données à utiliser et calculez le lift à partir des probabilités prévues pour les données qui ne sont pas dans l’estimation du modèle.
Notation
| Terme | Description |
|---|---|
| d | nombre de cas dans 10 % des données |
 | probabilité prévue de l’événement |
 | probabilité de l’événement dans les données d’apprentissage ou, si l’analyse n’utilise aucune validation, dans l’ensemble de données complet |
Coût de mauvais classement
Le coût de mauvais classement du tableau récapitulatif du modèle est le coût relatif de mauvais classement pour le modèle par rapport à un classificateur sans importance qui classe toutes les observations dans la classe la plus fréquente.
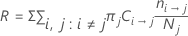
La formule suivante correspond au coût relatif de mauvais classement :
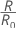
où R0 est le coût pour le classificateur sans importance.
La formule de R est plus simple lorsque les probabilités a priori sont égales ou proviennent des données.
Probabilités a priori égales
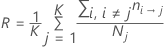
Probabilités a priori des données
Avec cette définition, R se calcule selon la formule suivante :
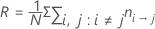
Notation
| Terme | Description |
|---|---|
| πj | probabilité a priori de la je classe de la variable de réponse |
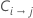 | coût de la classe de mauvais classement i comme classe j |
 | nombre d'enregistrements de classe i mal classés en classe j |
| Nj | nombre de cas dans la je classe de la variable de réponse |
| K | nombre de classes dans la variable de réponse |
| N | nombre de cas dans les données |
