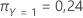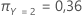Méthodes et formules pour les mauvais classements dans Classification CART^®

Sélectionnez la méthode ou la formule de votre choix.

Sur ce thème

Dénombrement
Dénombrement pondéré
% erreur
Coût

Le tableau de mauvais classement n’est pas présent lorsque la méthode de partition est la probabilité de classe.

Dénombrement

Lorsqu’il n’y a pas de pondération, les dénombrements et les effectifs d’échantillon sont identiques.

Dénombrement pondéré

Dans le cas pondéré, le dénombrement pondéré est la somme des pondérations d’une catégorie. Dénombrements pondérés arrondis au nombre entier le plus proche. Utilisez les pondérations non arrondies pour calculer les pourcentages et les taux. Prenons l'exemple simple suivant :

Niveau de réponse	Niveau prévu	Pondération
Oui	Oui	0,1
Oui	Oui	0,2
Oui	Non	0,3
Oui	Non	0,4
Non	Non	0,5
Non	Non	0,6
Non	Oui	0,7
Non	Oui	0,8

Ce tableau fournit les statistiques suivantes :

Classe réelle	Dénombrement pondéré	Mal classé	Classe prévue = Non	Pourcentage correct
Oui	0,1 + 0,2 + 0,3 + 0,4 = 1	0,1 + 0,2 = 0,3 ≈ 0	0,3 + 0,4 = 0,7 ≈ 1	(0,3 / 1,0) ×100 = 30 %
Non	0,5 + 0,6 + 0,7 + 0,8 = 2,6 ≈ 3	0,7 + 0,8 = 1,5 ≈ 2	0,5 + 0,6 = 1,1 ≈ 1	1,1 / 2,6) × 100 = 42,31 %
Toutes	1 + 2,6 = 3,6 ≈ 4	0,3 + 1,5 = 1,8 ≈ 2	0,7 + 1,1 = 1,8 ≈ 2	(0,3 + 1,1) / 3,6 × 100 = 38,89 %

% erreur

Dans le cas pondéré, utilisez les dénombrements pondérés à la place des dénombrements.

Coût

Le calcul du coût change selon que la variable de réponse est binaire ou multinomiale.

Coût = (% erreur × Entrée coût de mauvais classement pour la classe) / 100

Variable de réponse binaire

L’équation suivante donne le coût pour la classe d’événement :

L’équation suivante donne le coût pour la classe de non-événement :

L’équation suivante donne le coût global pour toutes les classes :

Variable de réponse multinomiale

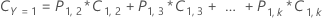
Pour le cas multinomial, l’équation étend la formule de la variable de réponse binaire pour tenir compte de tous les types possibles de mauvais classements. Par exemple, pour une réponse multinomiale avec des classes k, le coût de mauvais classement pour Y = 1 utilise l’équation suivante :

L’équation suivante donne le coût global pour le cas multinomial :

Prenons, par exemple, une variable de réponse avec 3 classes et les coûts de mauvais classement suivants :

	Classe prévue
Classe réelle	1	2	3
1	0,0	4,1	3,2
2	5,6	0,0	1,1
3	0,4	0,9	0,0

Ensuite, considérez que le tableau suivant donne les pourcentages d’erreur :

	Classe prévue
Classe réelle	1	2	3
1	N/A	1%	0,5 %
2	1,4%	N/A	2,1%
3	5%	1,2%	N/A

Enfin, considérez que les classes de la variable de réponse ont les probabilités a priori suivantes :

Les équations suivantes donnent les coûts associés au mauvais classement pour chaque classe dans la variable de réponse :

L’équation suivante donne le coût global :

Niveau de réponse	Niveau prévu	Pondération
Oui	Oui	0,1
Oui	Oui	0,2
Oui	Non	0,3
Oui	Non	0,4
Non	Non	0,5
Non	Non	0,6
Non	Oui	0,7
Non	Oui	0,8

Niveau de réponse	Niveau prévu	Pondération
Oui	Oui	0,1
Oui	Oui	0,2
Oui	Non	0,3
Oui	Non	0,4
Non	Non	0,5
Non	Non	0,6
Non	Oui	0,7
Non	Oui	0,8

Méthodes et formules pour les mauvais classements dans Classification CART®