Sur ce thème
Étape 1 : Étudier d’autres arbres
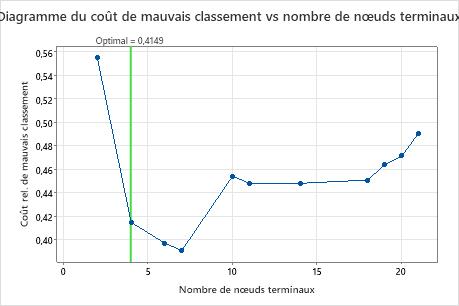
Le graphique Coût d’erreur de classification en fonction du nombre de nœuds terminaux affiche le coût d’erreur de classification pour chaque arbre dans la séquence qui produit l’arbre optimal. Par défaut, l’arbre optimal initial est le plus petit arbre avec un coût d’erreur de classification dans une erreur standard de l’arbre qui minimise le coût d’erreur de classification. Lorsque l’analyse utilise la validation croisée ou un ensemble de données de test, le coût de l’erreur de classification provient de l’échantillon de validation. Les coûts d’erreur de classification de l’échantillon de validation se stabilisent généralement et finissent par augmenter à mesure que l’arbre s’agrandit.
- L’arbre optimal fait partie d’un modèle lorsque les coûts de classification erronée diminuent. Un ou plusieurs arbres qui ont quelques nœuds supplémentaires font partie du même modèle. En règle générale, vous souhaitez effectuer des prédictions à partir d’un arbre avec la plus grande précision de prédiction possible. Si l’arborescence est suffisamment simple, vous pouvez également l’utiliser pour comprendre comment chaque variable de prédiction affecte les valeurs de réponse.
- L’arbre optimal fait partie d’un modèle lorsque les coûts de classification erronée sont relativement stables. Un ou plusieurs arbres avec des statistiques récapitulatives de modèle similaires ont beaucoup moins de nœuds que l’arbre optimal. En règle générale, un arbre avec moins de nœuds terminaux donne une image plus claire de la façon dont chaque variable de prédiction affecte les valeurs de réponse. Un arbre plus petit permet également d’identifier plus facilement quelques groupes cibles pour des études ultérieures. Si la différence de précision de prédiction pour un arbre plus petit est négligeable, vous pouvez également utiliser l’arbre plus petit pour évaluer les relations entre la réponse et les variables de prédiction.
Récapitulatif du modèle
| Nombre total de prédicteurs | 13 |
|---|---|
| Prédicteurs importants | 13 |
| Nombre de nœuds terminaux | 4 |
| Taille minimale du nœud terminal | 27 |
| Statistiques | Apprentissage | Test |
|---|---|---|
| Log de vraisemblance de moyenne | 0,4772 | 0,5164 |
| Zone située sous la courbe ROC | 0,8192 | 0,8001 |
| IC à 95 % | (0,3438; 1) | (0,7482; 0,8520) |
| Lift | 1,6189 | 1,8849 |
| Coût de mauvais classement | 0,3856 | 0,4149 |
Principaux résultats : Résumé du tracé et du modèle pour l’arbre à 4 nœuds
L’arbre de la séquence à 4 nœuds a un coût de classification erroné proche de 0,41. Le modèle lorsque le coût de la classification erronée diminue se poursuit après l’arborescence à 4 nœuds. Dans un cas comme celui-ci, les analystes choisissent d’explorer certains des autres arbres simples qui ont des coûts de classification erronée plus faibles.
Récapitulatif du modèle
| Nombre total de prédicteurs | 13 |
|---|---|
| Prédicteurs importants | 13 |
| Nombre de nœuds terminaux | 7 |
| Taille minimale du nœud terminal | 5 |
| Statistiques | Apprentissage | Test |
|---|---|---|
| Log de vraisemblance de moyenne | 0,3971 | 0,5094 |
| Zone située sous la courbe ROC | 0,8861 | 0,8200 |
| IC à 95 % | (0,5590; 1) | (0,7702; 0,8697) |
| Lift | 1,9376 | 1,8165 |
| Coût de mauvais classement | 0,2924 | 0,3909 |
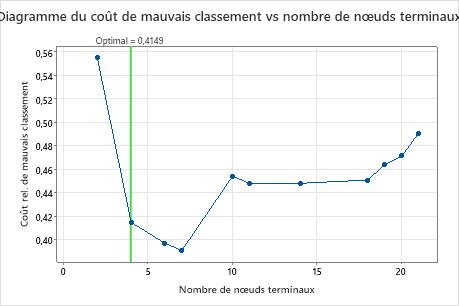
Principaux résultats : Résumé du tracé et du modèle pour l’arbre à 7 nœuds
L’arbre de classification qui minimise le coût relatif des erreurs de classification à validation croisée comporte 7 nœuds terminaux et un coût relatif des erreurs de classification d’environ 0,39. D’autres statistiques, telles que l’aire sous la courbe ROC, confirment également que l’arbre à 7 nœuds est plus performant que l’arbre à 4 nœuds. Étant donné que l’arbre à 7 nœuds a suffisamment de nœuds pour être facile à interpréter, les analystes décident d’utiliser l’arbre à 7 nœuds pour étudier les variables importantes et faire des prédictions.
Étape 2 : Examinez les nœuds terminaux les plus purs sur l’arborescence
Après avoir sélectionné une arborescence, examinez les nœuds terminaux les plus purs du diagramme. Le bleu représente le niveau de l’événement et le rouge représente le niveau du non-événement.
Remarque
Vous pouvez cliquer avec le bouton droit sur l’arborescence pour afficher la vue de division des nœuds de l’arborescence. Cette vue est utile lorsque vous disposez d’une arborescence volumineuse et que vous souhaitez voir uniquement les variables qui divisent les nœuds.
Les nœuds continuent de se diviser jusqu’à ce qu’ils ne puissent plus être divisés en d’autres groupes. Les nœuds qui sont principalement bleus indiquent une forte proportion du niveau de l’événement. Les nœuds qui sont principalement rouges indiquent une forte proportion du niveau de non-événement.
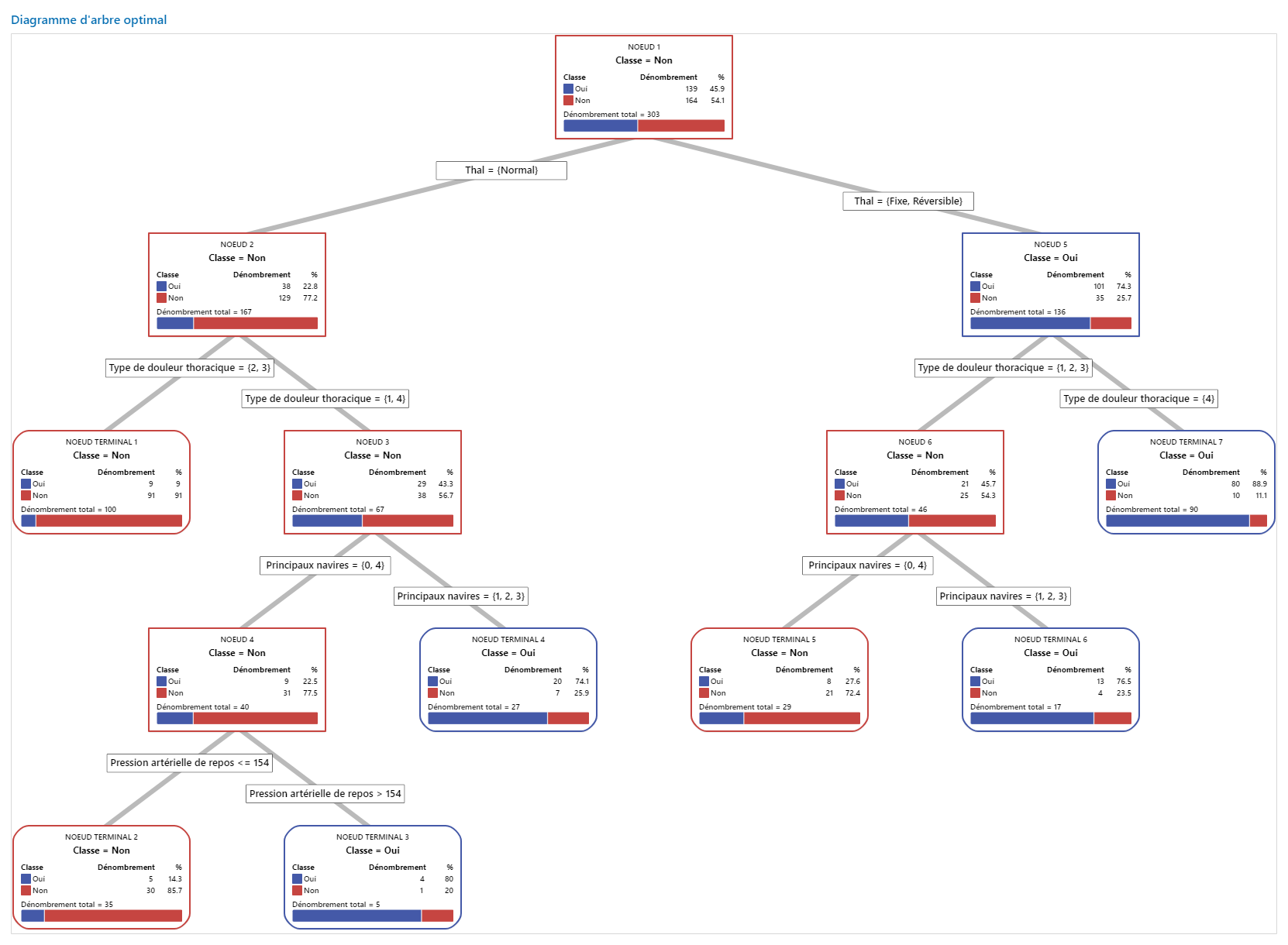
Résultat clé : Schéma arborescent
Cet arbre de classification comporte 7 nœuds terminaux. Le bleu correspond au niveau de l’événement (Oui) et le rouge au niveau non événementiel (Non). L’arborescence utilise l’ensemble de données d’entraînement. Vous pouvez basculer entre les vues de l’arborescence entre la vue détaillée et la vue fractionnée des nœuds.
- Nœud 2 : Le THAL était normal dans 167 cas. Sur les 167 cas, 38 (22,8 %) sont Oui, et 129 (77,2 %) sont Non.
- Nœud 5 : THAL était fixe ou réversible dans 136 cas. Sur les 136 cas, 101 (74,3%) sont Oui, et 35 (25,7%) sont Non.
Le séparateur suivant pour le nœud enfant gauche et le nœud enfant droit est le type de douleur thoracique, où la douleur est évaluée à 1, 2, 3 ou 4. Le nœud 2 est le parent du nœud terminal 1 et le nœud 5 est le parent du nœud terminal 7.
- Nœud terminal 1 : Dans 100 cas, le THAL était normal et la douleur thoracique était de 2 ou 3. Sur les 100 cas, 9 (9%) sont Oui, et 91 (91%) sont Non.
- Nœud terminal 7 : Dans 90 cas, le THAL était fixe ou réversible, et la douleur thoracique était de 4. Sur les 90 cas, 80 (88,9%) sont Oui, et 10 (11,1%) sont Non.
Étape 3 : Déterminer les variables importantes
Utilisez le graphique d’importance relative des variables pour déterminer quels prédicteurs sont les variables les plus importantes pour l’arborescence.
Les variables importantes sont des séparateurs primaires ou de substitution dans l’arbre. La variable ayant le score d’amélioration le plus élevé est définie comme la variable la plus importante et les autres variables sont classées en conséquence. L’importance des variables relatives normalise les valeurs d’importance pour faciliter l’interprétation. L’importance relative est définie comme le pourcentage d’amélioration par rapport au prédicteur le plus important.
Les valeurs d’importance relative des variables sont comprises entre 0 % et 100 %. La variable la plus importante a toujours une importance relative de 100 %. Si une variable n’est pas dans l’arbre, cette variable n’est pas importante.
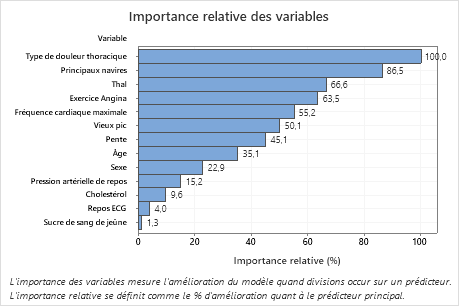
Résultat clé : Importance relative des variables
- Principaux navires est environ 87 % aussi important que Type de douleur thoracique.
- Thal et Exercice Angina sont tous deux environ 65 % aussi importants que Type de douleur thoracique.
- Fréquence cardiaque maximale est environ 55% aussi important que Type de douleur thoracique.
- Vieux pic est environ 50% aussi important que Type de douleur thoracique.
- Pente, Âge, Sexeet Pression artérielle de repos sont beaucoup moins importants que Type de douleur thoracique.
Bien qu’ils aient une importance positive, les analystes peuvent décider que Cholestérol, Repos ECG et Sucre de sang de jeûne ne sont pas des contributeurs importants à l’arbre.
Étape 4 : Évaluez le pouvoir prédictif de votre arbre
L’arbre le plus précis est celui dont le coût d’erreur de classification est le plus bas. Parfois, des arbres plus simples avec des coûts d’erreur de classification légèrement plus élevés fonctionnent tout aussi bien. Vous pouvez utiliser le graphique Coût d’erreur de classification par rapport aux nœuds terminaux pour identifier d’autres arbres.
La courbe ROC (Receiver Operating Characteristic) montre la qualité de classification des données par un arbre. La courbe ROC représente le taux de vrais positifs sur l’axe des y et le taux de faux positifs sur l’axe des x. Le vrai taux de positivité est également connu sous le nom de puissance. Le taux de faux positifs est également connu sous le nom d’erreur de type I.
Lorsqu’un arbre de classification peut parfaitement séparer les catégories dans la variable de réponse, l’aire sous la courbe ROC est 1, ce qui est le meilleur modèle de classification possible. Alternativement, si un arbre de classification ne peut pas distinguer les catégories et effectue des affectations de manière totalement aléatoire, alors l’aire sous la courbe ROC est de 0,5.
Lorsque vous utilisez une technique de validation pour créer l’arborescence, Minitab fournit des informations sur les performances de l’arborescence sur les données d’entraînement et de validation (test). Lorsque les courbes sont rapprochées, vous pouvez être plus sûr que l’arbre n’est pas trop ajusté. Les performances de l’arbre avec les données de test indiquent dans quelle mesure l’arbre peut prédire de nouvelles données.
- Taux de vrais positifs (TPR) : la probabilité qu’un cas d’événement soit prédit correctement
- Taux de faux positifs (FPR) : la probabilité qu’un cas non événementiel soit prédit de manière incorrecte
- Taux de faux négatifs (FNR) : probabilité qu’un cas d’événement soit prédit de manière incorrecte
- Taux vrai négatif (TNR) : probabilité qu’un cas non événementiel soit prédit correctement
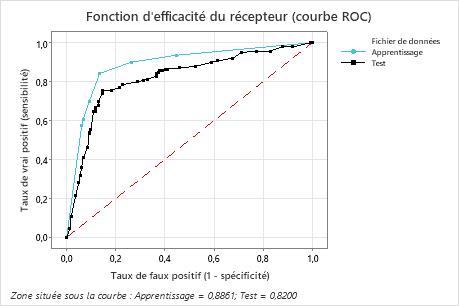
Résultat clé : Courbe ROC (Receiver Operating Characteristic)
Pour cet exemple, l’aire sous la courbe ROC est de 0,886 pour l’entraînement et de 0,82 pour le test. Ces valeurs indiquent que l’arbre de classification est un classificateur raisonnable, dans la plupart des applications.
Matrice de confusion
| Classe prévue (apprentissage) | |||||||
|---|---|---|---|---|---|---|---|
| Classe prévue (test) | |||||||
| Classe réelle | Dénombrement | Oui | Non | % correct | Oui | Non | % correct |
| Oui (Événement) | 139 | 117 | 22 | 84,2 | 105 | 34 | 75,5 |
| Non | 164 | 22 | 142 | 86,6 | 24 | 140 | 85,4 |
| Total | 303 | 139 | 164 | 85,5 | 129 | 174 | 80,9 |
| Statistiques | Apprentissage (%) | Test (%) |
|---|---|---|
| Taux de vrai positif (sensibilité ou puissance) | 84,2 | 75,5 |
| Taux de faux positif (erreur de type I) | 13,4 | 14,6 |
| Taux de faux négatif (erreur de type II) | 15,8 | 24,5 |
| Taux de vrai négatif (spécificité) | 86,6 | 85,4 |
Résultat clé : Matrice de confusion
- Taux de vrais positifs (TPR) : 84,2 % pour les données d’entraînement et 75,5 % pour les données de test
- Taux de faux positifs (FPR) : 13,4 % pour les données d’entraînement et 14,6 % pour les données de test
- Taux de faux négatifs (FNR) : 15,8 % pour les données d’entraînement et 24,5 % pour les données de test
- Taux de vrais négatifs (TNR) : 86,6 % pour les données d’entraînement et 85,4 % pour les données de test
Dans l’ensemble, le % de correction pour les données d’entraînement est de 85,5 % et de 80,9 % pour les données de test.
