Une probabilité a posteriori est la probabilité d'affectation des observations à des groupes d'après les données. Une probabilité a priori est la probabilité d'affectation d'une observation à un groupe avant la collecte des données. Par exemple, si vous classez les acheteurs d'une voiture spécifique, il se peut que vous sachiez déjà que 60 % des acheteurs sont des hommes et 40 % des femmes. Si vous connaissez ou pouvez estimer ces probabilités, l'analyse discriminante peut les utiliser pour calculer les probabilités a posteriori. Si vous n'indiquez aucune probabilité a priori, Minitab suppose que les groupes sont de probabilité égale.
En supposant que les données suivent une loi normale, la fonction discriminante linéaire est augmentée par ln(pi), où pi est la probabilité a priori du groupe i. Les observations étant affectées aux groupes sur la base de la plus petite distance généralisée, c'est-à-dire de la plus grande fonction discriminante linéaire, les probabilités a posteriori d'un groupe comportant une probabilité a priori élevée sont augmentées.
Remarque
Spécifier des probabilités a priori peut affecter considérablement l'exactitude des résultats. Etablissez si les proportions inégales entre les groupes traduisent une véritable différence dans la population réelle ou si la différence résulte d'une erreur d'échantillonnage.
Supposons maintenant que nous ayons des valeurs a priori et que fi(x) soit la densité jointe pour les données du groupe i (les paramètres de population étant remplacés par les estimations de l'échantillon).
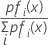
La probabilité a posteriori la plus grande est équivalente à la plus grande valeur de ln [pifi(x)]
Si fi(x) est la loi normale, alors :
ln [pifi(x)] = -0,5 [di2(x) – 2 ln pi] – (constante)
Le terme entre crochets est appelé distance quadratique généralisée de x pour le groupe i et est noté di2(x). Remarquez que :
di2(x) = -2[mi' Sp-1 x - 0,5 mi' Sp-1mi + ln pi] + x' Sp-1x
Le terme entre crochets est la fonction discriminante linéaire. La seule différence par rapport au cas dans lequel il n'existe pas de probabilité a priori est une modification du terme constant. Notez que le cas a posteriori le plus grand est équivalent à la plus petite distance généralisée, qui est elle-même équivalente à la plus grande fonction discriminante linéaire.
