Méthodes et formules pour la fonction Analyse des composantes principales

Dans l'analyse en composantes principales, Minitab détermine d'abord l'ensemble des valeurs propres orthogonales de la matrice de corrélation ou de covariance des variables. La matrice des composantes principales est égale au produit de la matrice des valeurs propres et de la matrice des variables indépendantes. La première composante principale rend compte du plus grand pourcentage de la variation totale des données. La deuxième composante principale rend compte du deuxième plus grand pourcentage de la variation totale des données, et ainsi de suite. L'objectif des composantes principales est d'expliquer la plus grande proportion possible de la variance par le plus petit nombre de composantes principales.

Les coefficients associés aux composantes principales sont uniques (excepté le signe qui peut changer) si les valeurs propres sont distinctes et différentes de zéro. Si une valeur propre se répète, l'espace couvert par tous les vecteurs de composantes principales correspondant à la même valeur propre est unique, mais les vecteurs individuels ne le sont pas. Ainsi, les coefficients affichés par Minitab dans les résultats et ceux figurant dans un ouvrage ou dans un autre programme peuvent ne pas concorder alors que les valeurs propres (variances des composantes) sont toujours les mêmes.

Si le nombre r de rangs dans la matrice de covariance est inférieur au nombre p de variables, il y aura p – r valeurs propres égales à zéro. Les vecteurs propres correspondant à ces valeurs propres peuvent ne pas être uniques. Cela peut se produire si le nombre d'observations est inférieur à p ou en cas de multicolinéarité.

Les vecteurs propres, constitués de coefficients correspondant à chaque variable, sont les pondérations associées à chaque variable utilisées pour calculer les scores des composantes principales. Les valeurs propres correspondent aux colonnes de la matrice orthogonale dans la décomposition spectrale de la matrice de covariance ou de corrélation, S ou R. Plus précisément, comme R est symétrique, il existe une matrice orthogonale V telle que V'RV = D ou, de manière équivalente, R = VDV', où D est une matrice diagonale dont les éléments diagonaux sont les valeurs propres. Les valeurs propres correspondent aux colonnes de V. Les valeurs propres proviennent de R = VDV'.

Notation

Formule

Les scores sont les combinaisons linéaires des variables d'origine qui rendent compte de la variance dans les données.

Les scores sont calculés de la manière suivante : Z = YV

Notation

Formule

Les valeurs propres correspondent aux éléments diagonaux de la matrice diagonale dans la décomposition spectrale de la matrice de covariance ou de corrélation (reportez-vous à la rubrique « Vecteurs propres »). Les valeurs propres représentent également les variances d'échantillon des composantes principales Z = V Y.

Notation

Formule

La proportion de la variance d'échantillon expliquée par la k^e composante principale est calculée de la manière suivante :

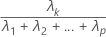
Notation

Terme	Description
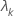	ke valeur propre
p	nombre de variables

Formule

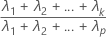
Notation

Terme	Description
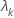	ke valeur propre
p	nombre de variables

Formule

La distance de Mahalanobis mesure la distance entre chaque point dans l'espace multivarié et la moyenne globale ou le point central, en utilisant la structure de covariance des données.

Minitab affiche une ligne de référence sur le diagramme des valeurs aberrantes pour mettre en évidence les valeurs aberrantes ayant de grandes valeurs de distance de Mahalanobis. Cette ligne de référence est définie par la formule suivante :

Quand n – p – 1 0, Minitab affiche le diagramme des valeurs aberrantes sans la ligne de référence.

Notation

Terme	Description
Yi	vecteur de valeur de données à la ligne i
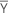	vecteur moyen
S-1	inverse de la matrice de covariance
p	nombre de variables
n	nombre de lignes non manquantes