Sur ce thème
Etape 1 : Déterminer le nombre de composantes principales
- Proportion de variance expliquée par les composantes
- Utilisez la proportion cumulée pour déterminer la part de la variance expliquée par les composantes principales. Conservez les composantes principales expliquant un niveau acceptable de variance. Le niveau acceptable dépend de votre étude. Pour une description, 80 % de la variance représentée peuvent suffire. En revanche, si vous souhaitez réaliser d'autres analyses sur les données, il peut être nécessaire que vos composantes principales expliquent au moins 90 % de la variance.
- Valeurs propres
- Vous pouvez vous fonder sur l'importance des valeurs propres pour déterminer le nombre de composantes principales. Conservez les composantes principales ayant les plus grandes valeurs propres. Par exemple, à l'aide du critère de Kaiser, vous utilisez uniquement les composantes principales dont les valeurs propres sont supérieures à 1.
- Diagramme en cône
- Le diagramme en cône organise les valeurs propres par ordre décroissant. Idéalement, la courbe doit d'abord décrire une pente forte, puis s'incurver avant de poursuivre en ligne droite. Utilisez les composantes correspondant à la partie abrupte de la courbe, c'est-à-dire avant le point marquant le début de la portion en ligne droite.
Analyse des valeurs et vecteurs propres de la matrice de corrélation
| Valeur propre | 3,5476 | 2,1320 | 1,0447 | 0,5315 | 0,4112 | 0,1665 | 0,1254 | 0,0411 |
|---|---|---|---|---|---|---|---|---|
| Proportion | 0,443 | 0,266 | 0,131 | 0,066 | 0,051 | 0,021 | 0,016 | 0,005 |
| Cumulée | 0,443 | 0,710 | 0,841 | 0,907 | 0,958 | 0,979 | 0,995 | 1,000 |
Vecteurs propres
| Variable | PC1 | PC2 | PC3 | PC4 | PC5 | PC6 | PC7 | PC8 |
|---|---|---|---|---|---|---|---|---|
| Revenu | 0,314 | 0,145 | -0,676 | -0,347 | -0,241 | 0,494 | 0,018 | -0,030 |
| Formation | 0,237 | 0,444 | -0,401 | 0,240 | 0,622 | -0,357 | 0,103 | 0,057 |
| Age | 0,484 | -0,135 | -0,004 | -0,212 | -0,175 | -0,487 | -0,657 | -0,052 |
| Résidence | 0,466 | -0,277 | 0,091 | 0,116 | -0,035 | -0,085 | 0,487 | -0,662 |
| Emploi | 0,459 | -0,304 | 0,122 | -0,017 | -0,014 | -0,023 | 0,368 | 0,739 |
| Epargne | 0,404 | 0,219 | 0,366 | 0,436 | 0,143 | 0,568 | -0,348 | -0,017 |
| Crédits | -0,067 | -0,585 | -0,078 | -0,281 | 0,681 | 0,245 | -0,196 | -0,075 |
| Cartes crédit | -0,123 | -0,452 | -0,468 | 0,703 | -0,195 | -0,022 | -0,158 | 0,058 |
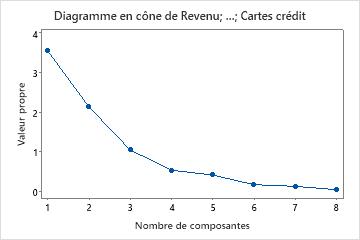
Résultats principaux : proportion cumulée, valeur propre, diagramme en cône
Dans ces résultats, les valeurs propres des trois premières composantes principales sont supérieures à 1. Ces trois composantes représentent 84,1 % de la variation des données. Le diagramme en cône indique que les valeurs propres commencent à former une ligne droite après la troisième composante principale. Si 84,1 % représente une part acceptable de la variation expliquée dans les données, vous devez utiliser les trois premières composantes principales.
Etape 2 : Interpréter chaque composante principale en fonction des variables initiales
Pour interpréter chaque composante principale, examinez la valeur et la direction des coefficients des variables initiales. Plus la valeur absolue du coefficient est élevée et plus la variable correspondante est importante dans le calcul de la composante. La valeur absolue à partir de laquelle un coefficient peut être considéré comme important est subjective. Vous devez faire appel à vos connaissances spécialisées pour déterminer à quel niveau la valeur de corrélation est importante.
Analyse des valeurs et vecteurs propres de la matrice de corrélation
| Valeur propre | 3,5476 | 2,1320 | 1,0447 | 0,5315 | 0,4112 | 0,1665 | 0,1254 | 0,0411 |
|---|---|---|---|---|---|---|---|---|
| Proportion | 0,443 | 0,266 | 0,131 | 0,066 | 0,051 | 0,021 | 0,016 | 0,005 |
| Cumulée | 0,443 | 0,710 | 0,841 | 0,907 | 0,958 | 0,979 | 0,995 | 1,000 |
Vecteurs propres
| Variable | PC1 | PC2 | PC3 | PC4 | PC5 | PC6 | PC7 | PC8 |
|---|---|---|---|---|---|---|---|---|
| Revenu | 0,314 | 0,145 | -0,676 | -0,347 | -0,241 | 0,494 | 0,018 | -0,030 |
| Formation | 0,237 | 0,444 | -0,401 | 0,240 | 0,622 | -0,357 | 0,103 | 0,057 |
| Age | 0,484 | -0,135 | -0,004 | -0,212 | -0,175 | -0,487 | -0,657 | -0,052 |
| Résidence | 0,466 | -0,277 | 0,091 | 0,116 | -0,035 | -0,085 | 0,487 | -0,662 |
| Emploi | 0,459 | -0,304 | 0,122 | -0,017 | -0,014 | -0,023 | 0,368 | 0,739 |
| Epargne | 0,404 | 0,219 | 0,366 | 0,436 | 0,143 | 0,568 | -0,348 | -0,017 |
| Crédits | -0,067 | -0,585 | -0,078 | -0,281 | 0,681 | 0,245 | -0,196 | -0,075 |
| Cartes crédit | -0,123 | -0,452 | -0,468 | 0,703 | -0,195 | -0,022 | -0,158 | 0,058 |
Résultats principaux : composante principale, diagramme des contributions
Dans ces résultats, la première composante principale présente une forte association positive avec Age, Résidence, Emploi et Epargne, et mesure donc principalement la stabilité financière à long terme. La deuxième composante présente une forte association négative avec Crédits et Cartes crédit, et mesure donc principalement l'historique de crédit du candidat. La troisième composante présente une forte association négative avec Revenu, Formation et Cartes crédit, et mesure donc principalement les qualifications du candidat en matière de formation et de revenus.
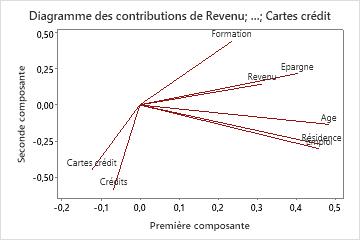
Le diagramme des contributions présente visuellement les résultats des deux premières composantes. Age, Résidence, Emploi et Epargne présentent tous une forte contribution positive à la composante 1, qui est donc une mesure de la stabilité financière à long terme. Les variables Crédits et Cartes crédit présentent chacune une forte contribution négative à la composante 2. Par conséquent, celle-ci mesure principalement l'historique de crédit du demandeur.
Etape 3 : Repérer les valeurs aberrantes
Utilisez le diagramme des valeurs aberrantes pour repérer les valeurs aberrantes. Tous les points situés au-dessus de la ligne de référence sont des valeurs aberrantes. Ces valeurs aberrantes peuvent avoir une incidence significative sur les résultats de l'analyse. Ainsi, si vous repérez une valeur aberrante dans vos données, vous devez examiner l'observation afin de comprendre ce qui la rend aberrante. Corrigez les erreurs de mesure ou d’entrée des données. Supprimez les données associées à des causes spéciales et procédez à une nouvelle analyse.
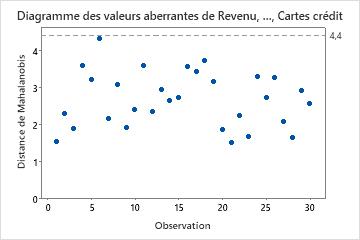
Résultats principaux : diagramme des valeurs aberrantes
On ne constate aucune valeur aberrante dans ces résultats. Tous les points sont situés en dessous de la ligne de référence.
Conseil
Maintenez le pointeur sur un point d'un diagramme des valeurs aberrantes pour identifier l'observation. Utilisez pour analyser plusieurs valeurs aberrantes sur le diagramme et marquer les observations dans la feuille de travail.
