Sur ce thème
Valeur propre
Les valeurs propres (également appelées valeurs caractéristiques ou racine latente) sont les variances des composantes principales.
Interprétation
Vous pouvez vous fonder sur l'importance des valeurs propres pour déterminer le nombre de composantes principales. Conservez les composantes principales ayant les plus grandes valeurs propres. Par exemple, à l'aide du critère de Kaiser, vous utilisez uniquement les composantes principales dont les valeurs propres sont supérieures à 1.
Pour comparer visuellement l'importance des valeurs propres, utilisez le diagramme en cône. Le diagramme en cône peut vous aider à déterminer le nombre de composantes en fonction de l'importance des valeurs propres.
Analyse des valeurs et vecteurs propres de la matrice de corrélation
| Valeur propre | 3,5476 | 2,1320 | 1,0447 | 0,5315 | 0,4112 | 0,1665 | 0,1254 | 0,0411 |
|---|---|---|---|---|---|---|---|---|
| Proportion | 0,443 | 0,266 | 0,131 | 0,066 | 0,051 | 0,021 | 0,016 | 0,005 |
| Cumulée | 0,443 | 0,710 | 0,841 | 0,907 | 0,958 | 0,979 | 0,995 | 1,000 |
Vecteurs propres
| Variable | PC1 | PC2 | PC3 | PC4 | PC5 | PC6 | PC7 | PC8 |
|---|---|---|---|---|---|---|---|---|
| Revenu | 0,314 | 0,145 | -0,676 | -0,347 | -0,241 | 0,494 | 0,018 | -0,030 |
| Formation | 0,237 | 0,444 | -0,401 | 0,240 | 0,622 | -0,357 | 0,103 | 0,057 |
| Age | 0,484 | -0,135 | -0,004 | -0,212 | -0,175 | -0,487 | -0,657 | -0,052 |
| Résidence | 0,466 | -0,277 | 0,091 | 0,116 | -0,035 | -0,085 | 0,487 | -0,662 |
| Emploi | 0,459 | -0,304 | 0,122 | -0,017 | -0,014 | -0,023 | 0,368 | 0,739 |
| Epargne | 0,404 | 0,219 | 0,366 | 0,436 | 0,143 | 0,568 | -0,348 | -0,017 |
| Crédits | -0,067 | -0,585 | -0,078 | -0,281 | 0,681 | 0,245 | -0,196 | -0,075 |
| Cartes crédit | -0,123 | -0,452 | -0,468 | 0,703 | -0,195 | -0,022 | -0,158 | 0,058 |
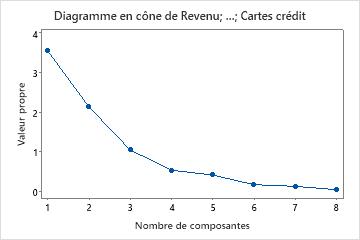
Dans ces résultats, les valeurs propres des trois premières composantes principales sont supérieures à 1. Ces trois composantes représentent 84,1 % de la variation des données. Le diagramme en cône indique que les valeurs propres commencent à former une ligne droite après la troisième composante principale. Si 84,1 % représente une part acceptable de la variation expliquée dans les données, vous devez utiliser les trois premières composantes principales.
Proportion
La valeur Proportion désigne la proportion de la variabilité des données expliquée par chaque composante principale.
Interprétation
Vous pouvez utiliser la proportion afin de déterminer quelles composantes principales expliquent la majeure partie de la variabilité dans les données. Plus la proportion est élevée, plus la composante principale explique une part importante de la variabilité. La valeur de proportion peut vous permettre de déterminer si la composante principale est suffisamment importante pour être conservée.
Par exemple, une composante principale avec une proportion de 0,621 explique 62,1 % de la variabilité des données. Par conséquent, cette composante doit être incluse. Une autre composante a une proportion de 0,005 et explique uniquement 0,5 % de la variabilité des données. Cette composante n'est sans doute pas suffisamment importante pour être incluse.
Cumulé
La valeur Cumulé est la proportion cumulée de la variabilité de l'échantillon représentée par des composantes principales consécutives.
Interprétation
Utilisez la proportion cumulée pour évaluer la part totale de la variance expliquée par les composantes principales consécutives. La proportion cumulée peut vous aider à déterminer le nombre de composantes principales à utiliser. Conservez les composantes principales expliquant un niveau acceptable de variance. Le niveau acceptable dépend de votre étude.
Par exemple, si vous les utilisez seulement à des fins descriptives, il peut vous suffire que les composantes principales n'expliquent que 80 % de la variance. En revanche, si vous souhaitez réaliser d'autres analyses sur les données, il peut être nécessaire que vos composantes principales expliquent au moins 90 % de la variance.
Composantes principales (CP)
Remarque
Si vous utilisez la matrice de corrélation, vous devez normaliser les variables pour obtenir le score correct des composantes.
Interprétation
Pour interpréter chaque composante principale, examinez la valeur et la direction des coefficients des variables initiales. Plus la valeur absolue du coefficient est élevée et plus la variable correspondante est importante dans le calcul de la composante. La valeur absolue à partir de laquelle un coefficient peut être considéré comme important est subjective. Vous devez faire appel à vos connaissances spécialisées pour déterminer à quel niveau la valeur de corrélation est importante.
Analyse des valeurs et vecteurs propres de la matrice de corrélation
| Valeur propre | 3,5476 | 2,1320 | 1,0447 | 0,5315 | 0,4112 | 0,1665 | 0,1254 | 0,0411 |
|---|---|---|---|---|---|---|---|---|
| Proportion | 0,443 | 0,266 | 0,131 | 0,066 | 0,051 | 0,021 | 0,016 | 0,005 |
| Cumulée | 0,443 | 0,710 | 0,841 | 0,907 | 0,958 | 0,979 | 0,995 | 1,000 |
Vecteurs propres
| Variable | PC1 | PC2 | PC3 | PC4 | PC5 | PC6 | PC7 | PC8 |
|---|---|---|---|---|---|---|---|---|
| Revenu | 0,314 | 0,145 | -0,676 | -0,347 | -0,241 | 0,494 | 0,018 | -0,030 |
| Formation | 0,237 | 0,444 | -0,401 | 0,240 | 0,622 | -0,357 | 0,103 | 0,057 |
| Age | 0,484 | -0,135 | -0,004 | -0,212 | -0,175 | -0,487 | -0,657 | -0,052 |
| Résidence | 0,466 | -0,277 | 0,091 | 0,116 | -0,035 | -0,085 | 0,487 | -0,662 |
| Emploi | 0,459 | -0,304 | 0,122 | -0,017 | -0,014 | -0,023 | 0,368 | 0,739 |
| Epargne | 0,404 | 0,219 | 0,366 | 0,436 | 0,143 | 0,568 | -0,348 | -0,017 |
| Crédits | -0,067 | -0,585 | -0,078 | -0,281 | 0,681 | 0,245 | -0,196 | -0,075 |
| Cartes crédit | -0,123 | -0,452 | -0,468 | 0,703 | -0,195 | -0,022 | -0,158 | 0,058 |
Dans ces résultats, la première composante principale présente une forte association positive avec Age, Résidence, Emploi et Epargne. Vous pouvez interpréter la composante comme étant principalement une mesure de la stabilité financière à long terme du candidat. La deuxième composante présente une forte association négative avec Crédits et Cartes crédit, et mesure donc principalement l'historique de crédit du candidat. La troisième composante présente une forte association négative avec Revenu, Formation et Cartes crédit, et mesure donc principalement les qualifications du candidat en matière de formation et de revenus.
Scores
Les scores sont des combinaisons linéaires des données déterminées par les coefficients associés à chaque composante principale. Pour obtenir le score d'une observation, vous devez indiquer chacune de ses valeurs dans l'équation linéaire de la composante principale. Si vous utilisez la matrice de corrélation, vous devez normaliser les variables pour obtenir le score correct des composantes avec l'équation linéaire.
Remarque
Pour obtenir le score calculé pour chaque observation, cliquez sur Stockage et indiquez une colonne afin de stocker les scores dans la feuille de travail lorsque vous réalisez l'analyse. Pour afficher les scores pour la première et la deuxième composantes sur un graphique, cliquez sur Graphiques et sélectionnez le diagramme des scores lorsque vous réalisez l'analyse.
Analyse des valeurs et vecteurs propres de la matrice de corrélation
| Valeur propre | 3,5476 | 2,1320 | 1,0447 | 0,5315 | 0,4112 | 0,1665 | 0,1254 | 0,0411 |
|---|---|---|---|---|---|---|---|---|
| Proportion | 0,443 | 0,266 | 0,131 | 0,066 | 0,051 | 0,021 | 0,016 | 0,005 |
| Cumulée | 0,443 | 0,710 | 0,841 | 0,907 | 0,958 | 0,979 | 0,995 | 1,000 |
Vecteurs propres
| Variable | PC1 | PC2 | PC3 | PC4 | PC5 | PC6 | PC7 | PC8 |
|---|---|---|---|---|---|---|---|---|
| Revenu | 0,314 | 0,145 | -0,676 | -0,347 | -0,241 | 0,494 | 0,018 | -0,030 |
| Formation | 0,237 | 0,444 | -0,401 | 0,240 | 0,622 | -0,357 | 0,103 | 0,057 |
| Age | 0,484 | -0,135 | -0,004 | -0,212 | -0,175 | -0,487 | -0,657 | -0,052 |
| Résidence | 0,466 | -0,277 | 0,091 | 0,116 | -0,035 | -0,085 | 0,487 | -0,662 |
| Emploi | 0,459 | -0,304 | 0,122 | -0,017 | -0,014 | -0,023 | 0,368 | 0,739 |
| Epargne | 0,404 | 0,219 | 0,366 | 0,436 | 0,143 | 0,568 | -0,348 | -0,017 |
| Crédits | -0,067 | -0,585 | -0,078 | -0,281 | 0,681 | 0,245 | -0,196 | -0,075 |
| Cartes crédit | -0,123 | -0,452 | -0,468 | 0,703 | -0,195 | -0,022 | -0,158 | 0,058 |
Dans ces résultats, le score pour la première composante principale peut être calculé à partir des données normalisées, à l'aide des coefficients fournis sous PC1 :
PC1 = Revenus 0,314 + Formation 0,237 + Age 0,484 + Adresse 0,466 + Emploi 0,459 + Epargne 0,404 - Crédits 0,067 - Cartes crédit 0,123
Distances
La distance de Mahalanobis est la distance entre un point de données et le centre d'un espace multivarié (la moyenne globale).
Remarque
Pour calculer la distance pour chaque observation, cliquez sur Stockage et indiquez une colonne de la feuille de travail afin de stocker les distances lorsque vous réalisez l'analyse. Pour afficher les distances sur un graphique, cliquez sur Graphiques et sélectionnez le diagramme des valeurs aberrantes lorsque vous réalisez l'analyse.
Interprétation
La distance de Mahalanobis permet de repérer les valeurs aberrantes. Etudier la distance de Mahalanobis est une méthode multivariée plus performante que l'examen des variables une par une pour détecter des valeurs aberrantes, car elle prend en compte les différentes échelles entre les variables, ainsi que leurs corrélations.
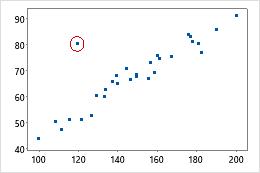
Par exemple, si vous les étudiez de façon indiviudelle, ni la valeur de x ni la valeur de y du point de données entouré ne sont aberrantes. En revanche, le point ne correspond pas à la structure de corrélation des deux variables. Par conséquent, la distance de Mahalanobis concernant ce point est anormalement grande.
Pour déterminer si une distance est suffisamment importante pour que l'observation soit considérée comme une valeur aberrante, utilisez le diagramme des valeurs aberrantes.
Diagramme en cône
Le diagramme en cône affiche les valeurs propres en fonction de chaque numéro de composante principale. Le diagramme en cône organise les valeurs propres par ordre décroissant. Les valeurs propres de la matrice de corrélation sont égales aux variances des composantes principales.
Pour afficher le diagramme en cône, cliquez sur Graphiques et sélectionnez le diagramme en cône lorsque vous réalisez l'analyse.
Interprétation

Le diagramme en cône indique que les valeurs propres commencent à décrire une ligne droite après la troisième composante principale. Par conséquent, les composantes principales restantes expliquent une très faible proportion de la variabilité (proche de zéro) et sont certainement sans importance.
Diagramme des scores
Le diagramme des scores affiche les scores de la deuxième composante principale par rapport à ceux de la première.
Pour afficher le diagramme des scores, cliquez sur Graphiques et sélectionnez le diagramme des scores lorsque vous réalisez l'analyse.
Interprétation
Si les deux premières composantes rendent compte de la majeure partie de la variance dans les données, vous pouvez utiliser le diagramme des scores pour évaluer la structure des données et détecter les groupes, les valeurs aberrantes et les tendances. La présence de regroupements de points sur le diagramme peut indiquer que les données présentent deux lois de distributions distinctes ou plus. Si les données suivent une loi normale et qu'il n'existe aucune valeur aberrante, les points sont distribués de manière aléatoire autour de zéro.
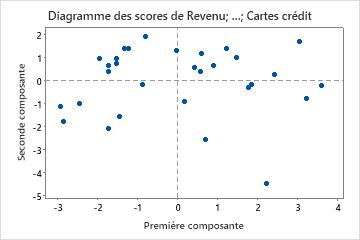
Dans le diagramme des scores, le point situé dans l'angle inférieur pourrait être une valeur aberrante. Vous devez examiner ce point.
Conseil
Pour afficher le score calculé de chaque observation, maintenez le pointeur sur un point du graphique. Pour créer des diagrammes des scores pour d'autres composantes, stockez les scores et utilisez .
Diagramme des contributions
Le diagramme des contributions représente les coefficients de chaque variable pour la première composante par rapport à ceux associés à la deuxième composante. Les coefficients sont les valeurs qui composent les vecteurs propres pour chaque composante principale. Les coefficients indiquent la pondération relative de chaque variable dans la composante.
Pour afficher le diagramme des contributions, cliquez sur Graphiques et sélectionnez le diagramme des contributions lorsque vous réalisez l'analyse.
Interprétation
Utilisez le diagramme des contributions pour déterminer les variables qui ont la plus grande incidence sur chaque composante. Les coefficients peuvent être compris entre -1 et 1. Des coefficients proches de -1 ou 1 indiquent que la variable influence fortement la composante. Des coefficients proches de 0 indiquent que la variable a une faible influence sur la composante. L’évaluation des coefficients peut également vous aider à caractériser chaque composante en fonction des variables.
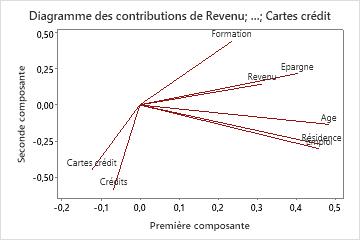
Dans le diagramme de coefficients, Age, Résidence, Emploi et Epargne présentent tous une forte contribution positive à la composante 1. Par conséquent, celle-ci mesure principalement la stabilité financière du demandeur. Les dettes et les cartes de crédit ont des coefficients négatifs importants sur la composante 2, de sorte que cette composante mesure principalement les antécédents de crédit d’un demandeur.
Diagramme de double projection
Le diagramme de double projection superpose le diagramme des scores et le diagramme des contributions.
Pour afficher le diagramme de double projection, cliquez sur Graphiques et sélectionnez le diagramme de double projection lorsque vous réalisez l'analyse.
Interprétation
Utilisez le diagramme de double projection pour évaluer la structure des données et les contributions des deux premières composantes sur un même graphique. Minitab représente les scores de la deuxième composante principale en fonction de ceux de la première, ainsi que les contributions pour les deux composantes.
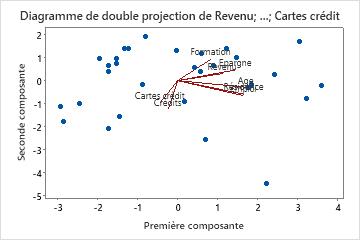
- Age, Résidence, Emploi et Epargne présentent tous une forte contribution positive à la composante 1. Par conséquent, celle-ci porte sur la stabilité financière à long terme du demandeur.
- Crédits et Cartes crédit présentent chacune une forte contribution négative à la composante 2. Par conséquent, celle-ci porte sur l'historique de crédit du demandeur.
- Le point situé dans l'angle inférieur droit peut être une valeur aberrante. Vous devez examiner ce point.
Diagramme des valeurs aberrantes
Le diagramme des valeurs aberrantes affiche la distance de Mahalanobis pour chaque observation, ainsi qu'une ligne de référence permettent de détecter les valeurs aberrantes. La distance de Mahalanobis est la distance entre chaque point de données et le centre d'un espace multivarié (la moyenne globale). Etudier les distances de Mahalanobis est une méthode multivariée plus performante que l'examen des variables une par une pour détecter des valeurs aberrantes, car elle prend en compte les différentes échelles entre les variables, ainsi que leurs corrélations.
Pour afficher le diagramme des valeurs aberrantes, vous devez cliquer sur Graphiques et sélectionner le diagramme des valeurs aberrantes lorsque vous réalisez l'analyse.
Interprétation
Utilisez le diagramme des valeurs aberrantes pour repérer les valeurs aberrantes. Tous les points situés au-dessus de la ligne de référence sont des valeurs aberrantes.
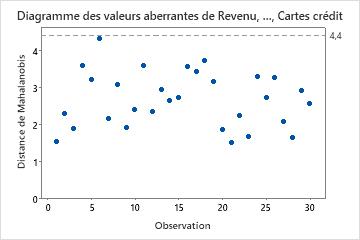
On ne constate aucune valeur aberrante dans ces résultats. Tous les points sont situés en dessous de la ligne de référence.
Conseil
Maintenez le pointeur sur un point d'un diagramme des valeurs aberrantes pour identifier l'observation. Utilisez pour analyser plusieurs valeurs aberrantes sur le diagramme et marquer les observations dans la feuille de travail.
