Sur ce thème
Covariance
Formule
Pour deux items x et y, la covariance est calculée comme suit :
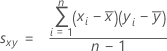
Notation
| Terme | Description |
|---|---|
 | moyenne d'échantillon du premier item |
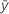 | moyenne d'échantillon du deuxième item |
| n | longueur de la colonne |
Corrélation
Formule
Pour deux items x et y, la corrélation est calculée comme suit :
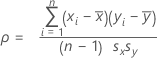
Dans le tableau des statistiques d'item omises, la corrélation ajustée aux items est la corrélation entre les scores de l'item omis et le score total de tous les autres items.
Notation
| Terme | Description |
|---|---|
 | moyenne d'échantillon du premier item |
| sx | écart type pour le premier item |
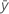 | moyenne d'échantillon du deuxième item |
| sy | écart type pour le deuxième item |
| n | longueur de la colonne |
Corrélation multiple quadratique
Formule
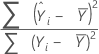
Notation
| Terme | Description |
|---|---|
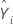 | ie score prévu pour l'item omis en utilisant l'équation de régression issue des items restants dans l'analyse |
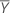 | moyenne des scores observés de l'item omis |
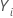 | ie score observé sur l'item omis |
Alpha de Cronbach
Formule
L'alpha de Cronbach pour tous les items est calculé comme suit :
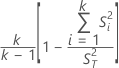
L'alpha de Cronbach après omission d'un item est calculé comme suit :
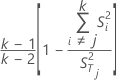
Notation
| Terme | Description |
|---|---|
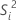 | variance d'échantillon du ie item |
 | variance d'échantillon du total |
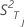 | variance d'échantillon du total calculée après omission du je item |
| T | scores totaux |
| k | nombre d'items dans l'analyse |
Moyenne
La moyenne d'un item est la somme de tous les scores d'un item divisée par le nombre de scores pour cet item.
La moyenne totale est la somme de toutes les moyennes d'item.
La moyenne totale ajustée est la somme de toutes les moyennes d'item, en excluant celle de l'item omis.
Ecart type
Formule
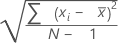
L'écart type d'un item est la racine carrée de la moyenne des écarts au carré des scores de cet item par rapport à la moyenne des items.
L'écart type de la moyenne totale est la racine carré de la moyenne des écarts au carré de tous les scores par rapport au score moyen total.
L'écart type total ajusté est l'écart type du score total après omission d'un item.
Notation
| Terme | Description |
|---|---|
| xi | ie observation |
 | moyenne des observations |
| N | nombre d'observations présentes |
Total
Le total représente la somme des scores de tous les items pour une seule observation (ligne). Par exemple, si les scores des items pour un participant donné à l'enquête sont 2, 5 et 3, le total pour l'observation est de 10.
