Matrice du plan
Minitab crée d'abord une matrice du plan d'expériences à partir des facteurs et du modèle que vous spécifiez. Les colonnes de cette matrice représentent les termes du modèle. Minitab ajoute ensuite des colonnes supplémentaires pour le terme constant, les blocs et les termes d'ordre supérieur pour exécuter la matrice du plan d'expériences pour le modèle de l'analyse.
Plans avec l'ensemble des facteurs continus
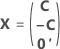
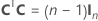
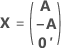
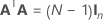
La matrice du plan complet comporte des colonnes en plus des colonnes représentant les facteurs. La matrice du plan d'expériences comporte une colonne de 1 pour le terme constant. La matrice du plan complet comporte également des colonnes qui représentent tout carré ou terme d'interaction dans le modèle.
Plans avec facteurs de catégorie
Dans un plan incluant des facteurs de catégorie, Minitab remplace la ligne de point central unique de la matrice du plan d'expériences par 2 pseudo-points centraux. Si le plan comporte uniquement 1 facteur de catégorie, il n'existe que deux pseudo-points centraux possibles. Les deux points se trouvent donc dans le plan.
Dans les cas où le plan comporte plus de 2 facteurs de catégorie, Minitab utilise un algorithme itératif pour sélectionner 2 pseudo-points centraux à inclure. L'algorithme cherche à minimiser la variance des coefficients de régression pour les effets linéaires du modèle.
Notation
| Terme | Description |
|---|---|
| C | Matrice en C |
| 0' | Ligne de zéros dans une matrice représentant un essai de point central |
| In | matrice identité n × n |
| A | Matrice correspondant à un sous-ensemble d'une matrice en C avec N lignes et n colonnes où  |
| N | Nombre de lignes dans le sous-ensemble des colonnes de la matrice en C |
| n | Nombre de facteurs inclus dans le plan |
Coefficient (Coeff)
Pour la matrice, voici la formule permettant de calculer le vecteur des coefficients dans le modèle :

Notation
| Terme | Description |
|---|---|
| X | matrice du plan |
| Y | vecteur de réponse |
Transformation de Box-Cox
La transformation de Box-Cox sélectionne les valeurs lambda (comme indiqué ci-dessous) qui minimisent la somme des carrés des valeurs résiduelles. La transformation obtenue est Y λ lorsque λ ≠ 0, et ln(Y) lorsque λ = 0. Lorsque λ < 0, Minitab multiplie également la réponse transformée par −1 pour conserver l'ordre de la réponse non transformée.
Minitab recherche une valeur optimale entre −2 et 2. Les valeurs en dehors de cet intervalle sont susceptibles de ne pas fournir un meilleur ajustement.
Voici quelques transformations courantes dans lesquelles Y′ représente la transformation des données Y :
| Valeur lambda (λ) | Transformation |
|---|---|
| λ = 2 | Y′ = Y 2 |
| λ = 0,5 | Y′ = 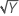 |
| λ = 0 | Y′ = ln(Y ) |
| λ = −0,5 |  |
| λ = −1 | Y′ = −1 / Y |
Régression pondérée
La régression par les moindres carrés pondérée est une méthode permettant de traiter les observations qui présentent des variances non constantes. Si les variances ne sont pas constantes, attribuez :
- des pondérations relativement faibles aux observations ayant des variances importantes
- des pondérations relativement importantes aux observations ayant des variances faibles
Les pondérations sont généralement choisies comme l'inverse de la variance de l'erreur pure dans le réponse.
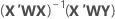
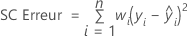
Notation
| Terme | Description |
|---|---|
| X | matrice du plan |
| X' | transposition de la matrice de plan |
| W | matrice n x n, avec les pondérations sur la diagonale |
| Y | vecteur des valeurs de réponse |
| n | nombre d'observations |
| wi | pondération pour l'ie observation |
| yi | valeur de réponse pour l'ie observation |
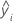 | valeur ajustée pour l'ie observation |
