Sur ce thème
Somme des carrés ajustée
Les sommes des carrés ajustées ne dépendent pas de l'ordre dans lequel les termes sont entrés dans le modèle. La somme des carrés ajustée est la proportion de variation expliquée par un terme, en tenant compte de tous les autres termes du modèle, indépendamment de l'ordre dans lequel ils ont été entrés.
Par exemple, dans le cas d'un modèle possédant trois facteurs X1, X2, et X3, la somme des carrés ajustée pour X2 indique la proportion de la variation restante expliquée par le terme de X2, du fait que les termes de X1 et X3 figurent également dans le modèle.
Les calculs des sommes des carrés ajustées pour trois facteurs sont les suivants :
- SCR (X3 | X1, X2) = SCE (X1, X2) - SCE (X1, X2, X3) ou
- SCR (X3 | X1, X2) = SCR (X1, X2, X3) - SCR (X1, X2)
où SCR (X3 | X1, X2) est la somme des carrés ajustée pour X3, sachant que X1 et X2 figurent dans le modèle.
- SCR (X2, X3 | X1) = SCE (X1) - SCE (X1, X2, X3) ou
- SCR (X2, X3 | X1) = SCR (X1, X2, X3) - SCR (X1)
où SCR (X2, X3 | X1) est la somme des carrés ajustée pour X2 et X3, sachant que X1 figure dans le modèle.
Vous pouvez étendre ces formules si votre modèle contient plus de 3 facteurs1.
- J. Neter, W. Wasserman and M.H. Kutner (1985). Applied Linear Statistical Models, Second Edition. Irwin, Inc.
Somme des carrés (SomCar)

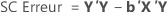
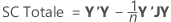
Minitab décompose la composante de modèle SomCar en indiquant la proportion de variation expliquée par chaque terme ou ensemble de termes, en utilisant à la fois la somme des carrés séquentielle et la somme des carrés ajustée.
Notation
| Terme | Description |
|---|---|
| b | vecteur des coefficients |
| X | matrice du plan |
| Y | vecteur des valeurs de réponse |
| n | nombre d'observations |
| J | matrice n sur n de 1s |
Somme des carrés séquentielle
Minitab répartit la composante de variance du modèle SomCar en sommes des carrés séquentielles pour chaque terme de facteur ou ensemble de termes de facteurs. La somme des carrés séquentielle dépend de l'ordre dans lequel les facteurs ou les prédicteurs sont entrés dans le modèle. La somme des carrés séquentielle est l'unique partie du modèle SomCar que chaque terme explique, en fonction des termes saisis précédemment.
Par exemple, dans le cas d'un modèle possédant trois facteurs X1, X2 et X3, la somme des carrés séquentielle pour X2 indique la proportion de la variation restante expliquée par X2, du fait que X1 figure déjà dans le modèle. Pour obtenir une séquence de termes différente, répétez l'analyse et entrez les facteurs dans un autre ordre.
Degrés de liberté (DL)
Différentes sommes des carrés ont des degrés de liberté différents.
DL pour un facteur numérique = 1
DL pour un facteur de catégorie = b − 1
DL pour un terme quadratique = 1
DL pour les blocs = c − 1
DL pour l'erreur = n - p
DL pour l'erreur pure = 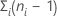
DL pour l'inadéquation de l'ajustement = m − p
DL total = n − 1
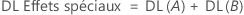
Remarque
Les facteurs de catégorie des plans de criblage dans Minitab comportent 2 niveaux. Ainsi, les degrés de liberté pour un facteur de catégorie sont 2 – 1 = 1. Par extension, les interactions entre les facteurs ont également 1 degré de liberté.
Notation
| Terme | Description |
|---|---|
| b | Nombre de niveaux du facteur |
| c | Nombre de blocs |
| n | Nombre total d'observations |
| ni | Nombre d'observations pour l'ie combinaison de niveaux de facteurs |
| m | Nombre de combinaisons de niveaux de facteurs |
| p | Nombre de coefficients |
CM ajust - Modèle

Notation
| Terme | Description |
|---|---|
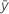 | Moyenne de la variable de réponse |
 | ie valeur ajustée de la réponse |
| p | Nombre de termes dans le modèle, terme de constante exclu |
CM ajust - Terme

CM ajust - Erreur
Le carré moyen de l'erreur (également abrégé en CM Erreur ou CME et noté s2) est la variance autour de la droite de régression. La formule est la suivante :

Notation
| Terme | Description |
|---|---|
| yi | ie valeur de réponse observée |
 | ième réponse ajustée |
| n | nombre d'observations |
| p | nombre de coefficients dans le modèle, constante non incluse |
F
Le calcul de la statistique F dépend du test d'hypothèse, comme suit :
- F(Terme)
-

- F(Inadéquation de l'ajustement)
-

Notation
| Terme | Description |
|---|---|
| CM ajust Terme | mesure de la variation expliquée par un terme après la prise en compte des autres termes du modèle |
| CM Erreur | mesure de la variation non expliquée par le modèle |
| CM Inadéquation de l'ajustement | mesure de la variation de la réponse qui peut être modélisée en ajoutant d'autres termes au modèle |
| CM Erreur pure | mesure de la variation des données de réponse répliquées |
- J. Neter, W. Wasserman et M.H. Kutner (1985). Applied Linear Statistical Models, 2e édition. Irwin, Inc.
Valeur de p - Tableau d'analyse de la variance
La valeur de p est une probabilité calculée à partir d'une loi F avec les degrés de liberté (DL) suivants :
- DL en numérateur
- somme des degrés de liberté pour le ou les termes du test
- DL en dénominateur
- degrés de liberté pour l'erreur
Formule
1 − P(F ≤ fj)
Notation
| Terme | Description |
|---|---|
| P(F ≤ f) | fonction de répartition de la loi F |
| f | statistique f pour le test |
Valeur de p - Test d'inadéquation de l'ajustement
- DL en numérateur
- degrés de liberté pour l'inéquation de l'ajustement
- DL en dénominateur
- degrés de liberté pour l'erreur pure
Formule
1 − P(F ≤ fj)
Notation
| Terme | Description |
|---|---|
| P(F ≤ fj) | fonction de répartition de la loi F |
| fj | statistique f pour le test |
