Sur ce thème
- Valeurs résiduelles de Pearson
- Valeurs résiduelles de Pearson normalisées et supprimées
- Valeurs résiduelles de la somme des carrés d'écart
- Valeurs résiduelles normalisées de la somme des carrés d'écart
- Valeurs résiduelles des sommes des carrés d'écart supprimées
- Khi deux du delta
- Somme des carrés d'écart du delta
- Bêta du delta (normalisé)
- Bêta du delta
- Effets de levier
- Distance de Cook
- DFITS
- Facteur d'inflation de la variance (FIV)
Valeurs résiduelles de Pearson
Eléments du Khi deux de Pearson permettant de détecter les combinaisons de facteurs/covariables qui ne sont pas ajustées correctement. Minitab stocke la valeur résiduelle de Pearson pour la ie combinaison de facteurs/covariables. La formule est la suivante :
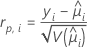
Notation
| Terme | Description |
|---|---|
| yi | valeur de la réponse pour la ie combinaison de facteurs/covariables |
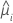 | valeur ajustée pour la ie combinaison de facteurs/covariables |
| V | fonction de variance pour le modèle à 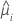 |
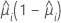
Valeurs résiduelles de Pearson normalisées et supprimées
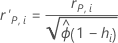
Notation
| Terme | Description |
|---|---|
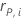 | valeur résiduelle de Pearson pour la ie combinaison de facteurs/covariables |
 | 1, pour les modèles binomiaux |
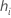 | effet de levier pour la ie combinaison de facteurs/covariables |
Valeurs résiduelles de la somme des carrés d'écart
Les valeurs résiduelles de la somme des carrés d'écart sont fondées sur la somme des carrés d’écart du modèle et permettent d'identifier les combinaisons de facteurs/covariables qui ne sont pas ajustées correctement. La somme des carrés d'écart du modèle est une statistique d'adéquation de l'ajustement qui repose sur la fonction de log de vraisemblance. La valeur résiduelle de la somme des carrés d'écart définie pour la ie combinaison de facteurs/covariables est la suivante :

Notation
| Terme | Description |
|---|---|
| yi | valeur de la réponse pour la ie combinaison de facteurs/covariables |
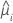 | valeur ajustée pour la ie combinaison de facteurs/covariables |
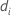 | somme des carrés d'écart pour la ie combinaison de facteurs/covariables |
Valeurs résiduelles normalisées de la somme des carrés d'écart

Notation
| Terme | Description |
|---|---|
| rD,i | Valeur résiduelle de la somme des carrés d'écart pour la ie combinaison de facteurs/covariables |
| hi | Effet de levier pour la ie combinaison de facteurs/covariables |
Valeurs résiduelles des sommes des carrés d'écart supprimées

Notation
| Terme | Description |
|---|---|
| yi | valeur de la réponse au niveau de la ie combinaison de facteurs/covariables |
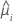 | valeur ajustée pour la ie combinaison de facteurs/covariables |
| hi | effet de levier pour la ie combinaison de facteurs/covariables |
| r'D,i | valeurs résiduelles normalisées de la somme des carrés d'écart pour la ie combinaison de facteurs/covariables |
| r'P,i | valeur résiduelle de Pearson normalisée pour la ie combinaison de facteurs/covariables |
1. Pregibon, D. (1981). "Logistic Regression Diagnostics", The Annals of Statistics, Vol. 9, No 4 pp. 705–724.
Khi deux du delta
Minitab calcule la variation dans le Khi deux de Pearson due à la suppression de toutes les observations avec la je combinaison de facteurs/covariables. Minitab stocke une valeur de Khi deux du delta pour chaque combinaison de facteurs/covariables dans les données. Vous pouvez utiliser le Khi deux du delta pour détecter les combinaisons de facteurs/covariables qui ne sont pas ajustées correctement. La formule pour le Khi deux du delta est la suivante :
Formule
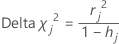
Notation
| Terme | Description |
|---|---|
| hj | effet de levier |
| rj | Valeurs résiduelles de Pearson |
Somme des carrés d'écart du delta
Minitab calcule la variation de la somme des carrés d'écart en supprimant toutes les observations avec la je combinaison de facteurs/covariables. Minitab stocke une valeur pour chaque combinaison de facteurs/covariables dans les données. Vous pouvez utiliser la somme des carrés d'écart du delta pour détecter les combinaisons de facteurs/covariables qui ne sont pas ajustées correctement. La variance de la statistique de la somme des carrés d'écart est la suivante :
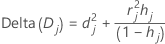
Notation
| Terme | Description |
|---|---|
| hj | effet de levier |
| rj | Valeurs résiduelles de Pearson |
| dj | valeurs résiduelles de la somme des carrés d'écart |
Bêta du delta (normalisé)
Minitab calcule la variation en supprimant toutes les observations avec la je combinaison de facteurs/covariables. Une valeur est stockée pour chaque combinaison de facteurs/covariables dans les données. Vous pouvez utiliser le β du delta normalisé pour détecter les combinaisons de facteurs/covariables qui influent fortement sur les estimations des coefficients. Cette valeur est fondée sur la valeur résiduelle de Pearson normalisée.
Formule
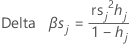
Notation
| Terme | Description |
|---|---|
| hj | effet de levier |
| rs j | valeurs résiduelles normalisées de Pearson |
Bêta du delta
Minitab calcule la variation en supprimant toutes les observations avec la je combinaison de facteurs/covariables. Une valeur est stockée pour chaque combinaison de facteurs/covariables dans les données. Vous pouvez utiliser le β du delta pour détecter les combinaisons de facteurs/covariables qui influent fortement sur les estimations des coefficients. Cette valeur est fondée sur la valeur résiduelle de Pearson.
Formule
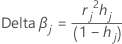
Notation
| Terme | Description |
|---|---|
| hj | effet de levier |
| rj | Valeurs résiduelles de Pearson |
Effets de levier
Les effets de levier représentent les éléments diagonaux de la matrice chapeau généralisée. Ils sont utiles pour détecter les combinaisons de facteurs/covariables susceptibles d'avoir une influence significative sur les résultats.
Formule
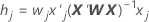
Notation
| Terme | Description |
|---|---|
| wj | je élément diagonal de la matrice de pondération issu de l'ajustement des coefficients |
| xj | je ligne de la matrice du plan |
| X | matrice du plan |
| X' | transposition de X |
| W | matrice de pondération issue de l'estimation des coefficients |
Distance de Cook
Formule
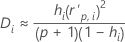
Notation
| Terme | Description |
|---|---|
| hi | effet de levier pour la ie combinaison de facteurs/covariables |
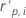 | valeur résiduelle de Pearson normalisée pour la ie combinaison de facteurs/covariables |
| p | degrés de liberté de la régression |
DFITS
Mesure de l'influence d'une suppression simple sur les valeurs ajustées. Les observations ayant des valeurs DFITS élevées peuvent constituer des valeurs aberrantes. Minitab calcule une valeur approximative pour DFITS.
Formule

Notation
| Terme | Description |
|---|---|
| hi | Effet de levier pour le point de données |
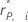 | Valeur résiduelle de Pearson supprimée pour le point de données |
Facteur d'inflation de la variance (FIV)

Notation
| Terme | Description |
|---|---|
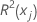 | coefficient de détermination avec xj comme variable de réponse et autres termes du modèle comme prédicteurs |
1. P. McCullagh et J.A. Nelder (1989), Generalized Linear Models, 2e édition, Chapman & Hall/CRC, Londres.
