Obtenez des définitions et des interprétations pour chaque statistique du tableau d'équation de régression.
Sur ce thème
Equations
Utilisez l'équation de régression pour décrire la relation entre la réponse et les termes du modèle. L'équation de régression est une représentation algébrique du modèle.
L'équation de régression de premier ordre avec une réponse binaire et plusieurs termes prend la forme suivante :

Si le modèle présente une courbure, un modèle polynomial d'un degré plus élevé est utilisé. Le modèle de second ordre est le suivant :
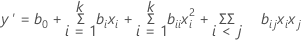
Dans l'équation de régression, les lettres représentent les éléments suivants :
- y' est la probabilité de l'événement, transformée avec la fonction de liaison
- b0 est la constante
- b1, b2, ..., bk sont les coefficients
- X1, X2, ..., Xk sont les valeurs des facteurs
Interprétation
Minitab affiche l'équation de régression en unités non codées, sauf si le modèle n'est pas hiérarchique.
Pour plus d'informations concernant la hiérarchie, consultez la rubrique Que sont les modèles hiérarchiques ?.
Remarque
Quand le modèle n'est pas hiérarchique, l'équation de régression utilise des unités codées.
- Interprétation des unités non codées
- Pour une équation de régression en unités non codées, interprétez les coefficients à l'aide des unités naturelles de chaque variable. Vous pouvez étudier les coefficients codés dans le tableau des coefficients. Le niveau inférieur d'un facteur de catégorie est −1 et le niveau supérieur est +1. Puisque l'équation est calculée en moyenne sur les blocs, elle ne contient aucun coefficient pour les blocs.
- Interprétation des unités codée
- Pour une équation de régression en unités codés, le niveau inférieur d'un facteur est −1 et le niveau supérieur est +1. Puisque l'équation est calculée en moyenne sur les blocs, elle ne contient aucun coefficient pour les blocs.
