Matrice du plan
Minitab génère une matrice de plan pour chaque plan. La première colonne correspond à une colonne de plan pour ce terme constant. Si le plan a été divisé en k blocs, il existera (k - 1) colonnes de blocs. Minitab utilise la même méthode de codage de blocs que pour les modèles factoriels. Ceci est suivi d'une colonne pour chaque effet principal. Les termes avec des facteurs de catégorie peuvent avoir plusieurs colonnes. Si le modèle contient des termes au carré, il existe une colonne pour chaque terme au carré. La colonne d'un terme au carré est le produit du facteur correspondant multiplié par lui-même. Si le modèle contient des termes d'interaction, il existe alors une colonne pour chaque terme d'interaction. Les interactions qui incluent des facteurs de catégorie peuvent avoir plusieurs colonnes. La colonne d'un terme d'interaction est le produit des deux colonnes croisées.
Si Minitab supprime certains termes, car les données ne peuvent pas les prendre en charge, ces termes n'apparaissent pas dans la matrice de plan stockée. Les colonnes stockées correspondent aux coefficients affichés.
Coefficient (Coeff)
Pour la matrice, voici la formule permettant de calculer le vecteur des coefficients dans le modèle :

Notation
| Terme | Description |
|---|---|
| X | matrice du plan |
| Y | vecteur de réponse |
Transformation de Box-Cox
La transformation de Box-Cox sélectionne les valeurs lambda (comme indiqué ci-dessous) qui minimisent la somme des carrés des valeurs résiduelles. La transformation obtenue est Y λ lorsque λ ≠ 0, et ln(Y) lorsque λ = 0. Lorsque λ < 0, Minitab multiplie également la réponse transformée par −1 pour conserver l'ordre de la réponse non transformée.
Minitab recherche une valeur optimale entre −2 et 2. Les valeurs en dehors de cet intervalle sont susceptibles de ne pas fournir un meilleur ajustement.
Voici quelques transformations courantes dans lesquelles Y′ représente la transformation des données Y :
| Valeur lambda (λ) | Transformation |
|---|---|
| λ = 2 | Y′ = Y 2 |
| λ = 0,5 | Y′ = 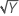 |
| λ = 0 | Y′ = ln(Y ) |
| λ = −0,5 |  |
| λ = −1 | Y′ = −1 / Y |
