Sur ce thème
Somme des carrés d'écart

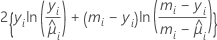
Les degrés de liberté du test dépendent de l'effectif d'échantillon et du nombre de termes dans le modèle :

Notation
| Terme | Description |
|---|---|
| Lf | log de vraisemblance pour le modèle complet |
| Lc | log de vraisemblance du modèle avec un sous-ensemble de termes issus du modèle complet |
| yi | nombre d'événements pour la ie ligne de données |
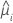 | réponse moyenne estimée pour la ie ligne de données |
| mi | nombre d'essais pour la ie ligne des données |
| n | nombre de lignes dans les données |
| p | degrés de liberté de la régression |
Pearson
La statistique du Khi deux de Pearson généralisée évalue la différence relative entre les valeurs observées et les valeurs ajustées.
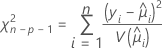
Les degrés de liberté du test dépendent de l'effectif d'échantillon et du nombre de termes dans le modèle. La statistique de Pearson a une loi du Khi deux exacte pour les données normales. Pour les données non normales, comme la loi binomiale ou la loi de Poisson, la statistique se rapproche asymptotiquement de la loi.
Notation
| Terme | Description |
|---|---|
| n | nombre de lignes dans les données |
| p | degrés de liberté de la régression |
| yi | valeur de la réponse pour la ie combinaison de facteurs/covariables |
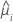 | réponse moyenne estimée de la ie ligne |
| V(·) | fonction de variance du modèle, définie ci-dessous |
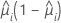
Hosmer-Lemeshow
La formule est :
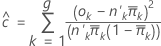
Pour former les groupes, Minitab classe les probabilités estimées dans l'ordre, puis tente de créer 10 groupes de taille égale.
Le nombre d'événements prévu dans un groupe est égal à :
événements prévus = 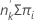
La valeur prévue pour le nombre de non-événements est égal à :
non-événements prévus = 
Notation
| Terme | Description |
|---|---|
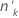 | nombre d'essais dans le ke groupe |
| ok | nombre d'événements parmi les 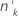 combinaisons de facteurs/covariables combinaisons de facteurs/covariables |
 | probabilité estimée moyenne pour chaque groupe |
| πi | probabilités ajustées pour les combinaisons de facteurs/covariables dans un groupe |
