Sur ce thème
- Etape 1 : Déterminer les termes qui ont le plus fort impact sur la réponse
- Etape 2 : Déterminer les termes qui ont des effets statistiquement significatifs sur la réponse
- Etape 3 : Déterminer les effets des prédicteurs
- Etape 4 : Déterminer l'ajustement du modèle à vos données
- Etape 5 : Déterminer si le modèle ne s'ajuste pas aux données
Etape 1 : Déterminer les termes qui ont le plus fort impact sur la réponse
Utilisez un diagramme de Pareto des effets normalisés pour comparer l'importance relative et la signification statistique des effets principaux, des effets quadratiques et des effets d'interaction.
Minitab présente les effets normalisés par ordre décroissant de leurs valeurs absolues. La ligne de référence du diagramme indique les effets significatifs. Par défaut, Minitab utilise un seuil de signification de 0,05 pour tracer la ligne de référence.
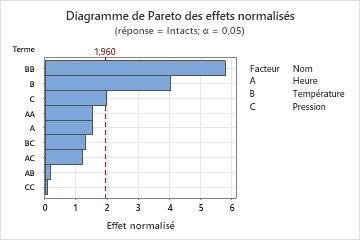
Résultats principaux : diagramme de Pareto
Dans ces résultats, le terme quadratique pour la température (BB), ainsi que les effets principaux pour la température (B) et la pression (C) sont significatifs au seuil de signification α de 0,05.
De plus, vous voyez que l'effet le plus important est celui du terme Température*Température (BB), car c'est celui qui a la barre la plus grande. Le terme Pression*Pression (CC) a le plus petit effet, étant donné que c'est celui qui a la barre la plus courte.
Etape 2 : Déterminer les termes qui ont des effets statistiquement significatifs sur la réponse
Pour déterminer si l'association entre la réponse et chacun des termes du modèle est statistiquement significative, comparez la valeur de p du terme à votre seuil de signification pour évaluer l'hypothèse nulle. L'hypothèse nulle est que le coefficient du terme est égal à zéro, ce qui implique qu'il n'existe aucune association entre le terme et la réponse. En général, un seuil de signification (noté alpha ou α) de 0,05 fonctionne bien. Un seuil de signification de 0,05 indique un risque de 5 % de conclure à tort qu'il existe une association.
- Valeur de p ≤ α : l'association est statistiquement significative
- Si la valeur de p est inférieure ou égale au seuil de signification, vous pouvez conclure qu'il existe une association statistiquement significative entre la variable de réponse et le terme.
- Valeur de p > α : l'association n'est pas statistiquement significative
- Si la valeur de p est supérieure au seuil de signification, vous ne pouvez pas conclure qu'il existe une association statistiquement significative entre la variable de réponse et le terme. Il est sans doute nécessaire de réajuster le modèle sans le terme.
- Si le coefficient d'un facteur est significatif, vous pouvez en conclure que la probabilité de l'événement n'est pas la même pour tous les niveaux du facteur.
- Si le coefficient d'un terme au carré est significatif, vous pouvez en conclure que la relation entre le facteur et la réponse suit une ligne courbe.
- Si un coefficient d'un terme d'interaction est significatif, la relation entre l'un des facteurs et la réponse dépend des autres facteurs du terme. Dans ce cas, vous ne devez pas interpréter les effets principaux sans prendre en compte l'effet d'interaction.
- Si le coefficient d'un bloc est statistiquement significatif, vous pouvez en conclure que la fonction de liaison du bloc est différente de la valeur moyenne.
Coefficients codés
| Terme | Coeff | Coef ErT | FIV |
|---|---|---|---|
| Constante | 3,021 | 0,384 | |
| Heure | 0,210 | 0,139 | 18,53 |
| Température | 0,641 | 0,159 | 19,53 |
| Pression | 0,420 | 0,211 | 70,48 |
| Heure*Heure | -0,0735 | 0,0482 | 1,01 |
| Température*Température | 0,2988 | 0,0517 | 1,17 |
| Pression*Pression | -0,0022 | 0,0277 | 70,24 |
| Heure*Température | -0,0092 | 0,0505 | 1,14 |
| Heure*Pression | 0,0417 | 0,0342 | 18,12 |
| Température*Pression | -0,0521 | 0,0396 | 19,24 |
Résultats principaux : coefficients
Dans ces résultats, les coefficients des effets principaux de Temps, Température et Pression sont des nombres positifs. Le coefficient du terme quadratique Temps*Temps est un nombre négatif. En général, les coefficients positifs augmentent la probabilité de l'événement tandis que les coefficients négatifs la réduisent quand la valeur du terme augmente.
Analyse de la variance
| Source | DL | Somme des carrés des écarts ajustée | Moyenne ajustée | Khi deux | Valeur de p |
|---|---|---|---|---|---|
| Modèle | 9 | 903,478 | 100,386 | 903,48 | 0,000 |
| Heure | 1 | 2,303 | 2,303 | 2,30 | 0,129 |
| Température | 1 | 16,388 | 16,388 | 16,39 | 0,000 |
| Pression | 1 | 3,966 | 3,966 | 3,97 | 0,046 |
| Heure*Heure | 1 | 2,331 | 2,331 | 2,33 | 0,127 |
| Température*Température | 1 | 34,012 | 34,012 | 34,01 | 0,000 |
| Pression*Pression | 1 | 0,006 | 0,006 | 0,01 | 0,937 |
| Heure*Température | 1 | 0,033 | 0,033 | 0,03 | 0,856 |
| Heure*Pression | 1 | 1,490 | 1,490 | 1,49 | 0,222 |
| Température*Pression | 1 | 1,731 | 1,731 | 1,73 | 0,188 |
| Erreur | 5 | 23,404 | 4,681 | ||
| Total | 14 | 926,882 |
Résultats principaux : valeur de p
Dans ces résultats, le terme quadratique Température*Température, ainsi que les effets principaux pour la température et la pression sont significatifs au seuil de signification α de 0,05.
Etape 3 : Déterminer les effets des prédicteurs
- Rapports des probabilités de succès pour les prédicteurs continus
-
Les rapports de probabilités de succès supérieurs à 1 indiquent que l'événement est plus susceptible de se produire à mesure que le prédicteur augmente. Les rapports de probabilités de succès inférieurs à 1 indiquent que l'événement est moins susceptible de se produire à mesure que le prédicteur augmente.
Rapports des probabilités de succès pour les prédicteurs continus
Incrément Rapport des
probabilités
de succèsIC à 95 % Dose (mg) 0,5 6,1279 (1,7218; 21,8087) Résultat principal : rapport des probabilités de succès
Dans ces résultats, le modèle utilise le dosage d'un médicament pour prévoir la présence ou l'absence de bactérie chez des sujets adultes. Dans cet exemple, l'absence de bactérie constitue l'événement. Chaque comprimé contenant une dose de 0,5 mg, les chercheurs utilisent une variation d'unité de 0,5 mg. Le rapport des probabilités de succès est environ de 6. Pour chaque comprimé supplémentaire pris par un adulte, les probabilités de succès concernant le fait qu'un patient n'ait pas la bactérie sont multipliées par 6.
- Rapports des probabilités de succès pour les prédicteurs de catégorie
-
Pour les prédicteurs de catégorie, le rapport des probabilités de succès compare les probabilités qu'un événement se produise à deux niveaux différents du prédicteur. Minitab configure la comparaison en répertoriant les niveaux dans deux colonnes, Niveau A et Niveau B. Le niveau B est le niveau de référence du facteur. Les rapports des probabilités de succès supérieurs à 1 indiquent que l'événement est plus susceptible de se produire au niveau A. Les rapports des probabilités de succès inférieurs à 1 indiquent que l'événement est moins susceptible de se produire au niveau A. Pour plus d'informations sur le codage des prédicteurs de catégorie, reportez-vous à la rubrique Schémas de codage des prédicteurs de catégorie.
Rapports des probabilités de succès pour les prédicteurs de catégorie
Niveau A Niveau B Rapport des
probabilités
de succèsIC à 95 % Mois 2 1 1,1250 (0,0600; 21,0834) 3 1 3,3750 (0,2897; 39,3165) 4 1 7,7143 (0,7461; 79,7592) 5 1 2,2500 (0,1107; 45,7172) 6 1 6,0000 (0,5322; 67,6397) 3 2 3,0000 (0,2547; 35,3325) 4 2 6,8571 (0,6556; 71,7169) 5 2 2,0000 (0,0976; 41,0019) 6 2 5,3333 (0,4679; 60,7946) 4 3 2,2857 (0,4103; 12,7323) 5 3 0,6667 (0,0514; 8,6389) 6 3 1,7778 (0,2842; 11,1200) 5 4 0,2917 (0,0252; 3,3719) 6 4 0,7778 (0,1464; 4,1326) 6 5 2,6667 (0,2124; 33,4861) Résultat principal : rapport des probabilités de succès
Dans ces résultats, le prédicteur de catégorie est le premier mois de la haute saison d'un hôtel. La réponse correspond à l'annulation ou non d'une réservation par un client. Dans cet exemple, une annulation constitue l'événement. Le plus grand rapport des probabilités de succès est d'environ 7,71, lorsque le niveau A est le mois 4 et le niveau B est le mois 1. Cela indique que la probabilité qu'un client annule une réservation pendant le mois 4 est environ 8 fois supérieure à la probabilité qu'un client annule une réservation pendant le mois 1.
Etape 4 : Déterminer l'ajustement du modèle à vos données
Remarque
De nombreuses statistiques récapitulatives du modèle et d'adéquation de l'ajustement sont influencées par la façon dont les données sont organisées dans la feuille de travail et par le nombre d'essais contenus dans chaque ligne (un ou plusieurs). Le test de Hosmer-Lemeshow n'est pas influencé par l'organisation des données et présente des résultats comparables que les lignes contiennent un ou plusieurs essais. Pour plus d'informations, reportez-vous à la rubrique Influence du format des données sur l'ajustement dans la régression logistique binaire.
- R carré de la somme des carrés d'écart
-
Plus le R2 de la somme des carrés d'écart est élevé, plus le modèle est ajusté à vos données. Le R2 de la somme des carrés d'écart est toujours compris entre 0 et 100 %.
Le R2 de la somme des carrés d'écart augmente toujours lorsque vous ajoutez des termes à un modèle. Par exemple, le meilleur modèle à 5 termes aura toujours une valeur R2 au moins aussi élevée que celle du meilleur modèle à 4 termes. Par conséquent, le R2 de la somme des carrés d'écart est surtout utile pour comparer des modèles de même taille.
La disposition des données a un impact sur le R2 de la somme des carrés d'écart. Le R2 de la somme des carrés d'écart est généralement plus élevé pour des données avec plusieurs essais par ligne que pour des données avec un seul essai par ligne. Les R2 de la somme des carrés d'écart sont comparables uniquement entre des modèles qui utilisent le même format de données.
Les statistiques d'adéquation de l'ajustement ne sont qu'un des types de mesures permettant d'évaluer l'ajustement du modèle. Même si un modèle présente une valeur souhaitée, vous devez consulter les graphiques des valeurs résiduelles et les tests d'adéquation de l'ajustement pour évaluer l'ajustement du modèle aux données.
- R carré (ajust) de la somme des carrés d'écart
-
Pour comparer des modèles n'ayant pas le même nombre de termes, utilisez le R2 ajusté de la somme des carrés d'écart. Celui-ci augmente toujours lorsque vous ajoutez un terme au modèle. Le R2 ajusté de la somme des carrés d'écart intègre le nombre de termes dans le modèle pour vous aider à choisir le modèle correct.
- AIC, AICc et BIC
-
Utilisez les valeurs AIC, AICc et BIC pour comparer différents modèles. Des valeurs faibles sont souhaitables pour chacune. Cependant, le modèle présentant la valeur la plus faible pour un ensemble de prédicteurs n'est pas forcément bien ajusté aux données. Vous devez aussi utiliser les graphiques des valeurs résiduelles et les tests d'adéquation de l'ajustement pour évaluer l'ajustement du modèle aux données.
Récapitulatif du modèle
| R carré de la somme des carrés des écarts | R carré (ajust) de la somme des carrés des écarts | AIC | AICc | BIC |
|---|---|---|---|---|
| 97,95% | 76,75% | 105,98 | 171,98 | 114,48 |
Résultats principaux : R carré de la somme des carrés d'écart, R carré (ajust) de la somme des carrés d'écart, AIC
Dans ces résultats, le modèle explique 97,95 % de la somme des carrés des écarts dans la variable de réponse. Pour ces données, la valeur R2 de la somme des carrés des écarts indique que le modèle fournit un bon ajustement aux données. Si des modèles supplémentaires sont ajustés avec d'autres prédicteurs, utilisez la valeur R2 ajustée de la somme des carrés des écarts, ainsi que les valeurs AIC, AICc et BIC pour comparer l'ajustement des modèles aux données.
Etape 5 : Déterminer si le modèle ne s'ajuste pas aux données
- Fonction de liaison incorrecte
- Terme d'ordre supérieur omis pour les variables du modèle
- Prédicteur omis non présent dans le modèle
- Surdispersion
Si l'écart est statistiquement significatif, vous pouvez essayer une autre fonction de liaison ou modifier les termes du modèle.
- Somme des carrés des écarts : la valeur de p du test de la somme des carrés des écarts a tendance à être plus faible lorsque les lignes de données ne contiennent qu'un seul essai chacune que lorsqu'elles en contiennent plusieurs ; elle a également tendance à décroître lorsque le nombre d'essais par ligne diminue. Pour les données ne contenant qu'un essai par ligne, les résultats du test de Hosmer-Lemeshow sont plus fiables.
- Pearson : l'approximation de la loi du Khi deux utilisée par le test de Pearson est inexacte lorsque le nombre d'événements attendu par ligne est faible. Par conséquent, le test d'adéquation de l'ajustement de Pearson est inexact lorsque les lignes ne contiennent qu'un seul essai.
- Hosmer-Lemeshow : le test de Hosmer-Lemeshow ne dépend pas du nombre d'essais par ligne dans les données, contrairement aux autres tests d'adéquation de l'ajustement.Lorsque les données comptent plusieurs essais par ligne, le test de Hosmer-Lemeshow est un indicateur plus fiable de l'ajustement du modèle aux données.
Informations de réponse
| Variable | Valeur | Dénombrement | Nom d'événement |
|---|---|---|---|
| Pourrissement | Evénement | 506 | Event |
| Non-événement | 7482 | ||
| Conteneurs | Total | 7988 |
Tests d'adéquation de l'ajustement
| Test | DL | Khi deux | Valeur de p |
|---|---|---|---|
| Somme des carrés des écarts | 5 | 0,97 | 0,965 |
| Pearson | 5 | 0,97 | 0,965 |
| Hosmer-Lemeshow | 6 | 0,10 | 1,000 |
Résultats principaux pour le format événement/essai : informations sur la réponse, test de somme des carrés d'écart, test de Pearson, test de Hosmer-Lemeshow
Dans ces résultats, les tests d'adéquation de l'ajustement ont tous des valeurs de p supérieures au seuil de signification habituel de 0,05. Les tests ne permettent pas de conclure que les probabilités prévues diffèrent des probabilités observées d'une façon non prévue par la loi binomiale.
