Sur ce thème
Probabilité observée
La probabilité observée est le nombre d'événements divisé par le nombre d'essais. Par exemple, si le nombre d'événements est de 30 et le nombre d'essais de 495, la probabilité observée est donc de 0,06061.
Valeur ajustée
La valeur ajustée est également appelée probabilité de l'événement ou probabilité prévue. La probabilité d'un événement est la chance de survenue de l'événement expérimental spécifié. La probabilité d'événement estime la probabilité qu'un événement se produise, comme le fait de tirer un as dans un jeu de cartes ou la fabrication d'une pièce non conforme. La probabilité d'un événement est comprise entre 0 (impossible) et 1 (certain).
Interprétation
La réponse expérimentale ne peut avoir que deux valeurs, comme la présence ou l'absence d'une maladie particulière. La probabilité d'événement est la probabilité que la réponse pour un schéma de facteurs ou de covariables donnée se produise (par exemple, la probabilité qu'une femme de plus de 50 ans développe un diabète de type 2).
Chaque tentative d'une expérience est appelée "essai". Par exemple, si vous lancez une pièce 10 fois et que vous enregistrez le nombre de fois où elle tombe côté face, vous effectuez 10 essais pour cette expérience. Si les essais sont indépendants et de probabilité égale, vous pouvez estimer la probabilité d'événement en divisant le nombre d'événements par le nombre total d'essais. Par exemple, si la pièce tombe 6 fois côté face sur les 10 essais, la probabilité estimée de l'événement (nombre de chutes côté face) est égale à :
Nombre d'événements ÷ Nombre d'essais = 6 ÷ 10 = 0,6
ErT ajust
L'erreur type de l'ajustement (ErT ajust) estime la variation de la probabilité d'événement pour les paramètres de variables spécifiées. Le calcul de l'intervalle de confiance pour la probabilité d'événement utilise l'erreur type de la valeur ajustée. Les erreurs types ne sont jamais négatives.
Interprétation
Utilisez l'erreur type de l'ajustement pour mesurer la précision de l'estimation de la probabilité d'événement. Plus l'erreur type est faible, plus la prévision de la réponse moyenne est précise.
Par exemple, un chercheur s'intéresse aux facteurs d'inclusion dans une étude médicale. Pour un premier ensemble de facteurs, la probabilité qu'un patient remplisse les conditions de participation à une étude sur un nouveau traitement est de 0,63, avec une erreur type de 0,05. Pour un second ensemble de paramètres de facteurs, la probabilité est la même, mais avec une erreur type de 0,03. L'analyste peut affirmer avec plus de certitude que la probabilité d'événement est proche de 0,63 pour ce dernier.
Intervalle de confiance pour la valeur ajustée (IC à 95 %)
Ces intervalles de confiance (IC) sont des étendues de valeurs ayant de fortes chances de contenir la probabilité d'événement pour la population qui présente les valeurs observées pour les variables de prédiction du modèle.
Les échantillons étant aléatoires, il est peu probable que deux échantillons d'une population donnent des intervalles de confiance identiques. Cependant, si vous prélevez de nombreux échantillons, un certain pourcentage des intervalles de confiance obtenus contiendra le paramètre de population inconnu. Le pourcentage de ces intervalles de confiance contenant le paramètre est le niveau de confiance de l'intervalle.
- Estimation ponctuelle
- L'estimation ponctuelle est l'estimation du paramètre calculé à partir des données échantillons.
- Marge d'erreur
- La marge d'erreur définit la largeur de l'intervalle de confiance et dépend de l'étendue des probabilités d'événement, de l'effectif d'échantillon et du niveau de confiance.
Interprétation
Utilisez l'intervalle de confiance afin d'évaluer l'estimation de la valeur ajustée pour les valeurs observées des variables.
Par exemple, avec un niveau de confiance de 95 %, vous pouvez être sûr à 95 % que l'intervalle de confiance comprend la probabilité d'événement pour les valeurs indiquées des variables du modèle. L'intervalle de confiance vous aide à évaluer la signification pratique de vos résultats. Utilisez vos connaissances spécialisées pour déterminer si l'intervalle de confiance comporte des valeurs ayant une signification pratique pour votre situation. Si l'intervalle est trop grand pour être utile, vous devez sans doute augmenter votre effectif d'échantillon.
Val rés
La valeur résiduelle mesure la capacité de prévision de l'observation par le modèle. Par défaut, Minitab calcule les valeurs résiduelles des sommes des carrés d'écart. Les observations qui sont mal ajustées par le modèle ont des valeurs résiduelles de Pearson et des sommes des carrés d'écart élevées. Minitab calcule les valeurs résiduelles pour chaque combinaison distincte de facteurs/covariables.
Que vous utilisiez les valeurs résiduelles de la somme des carrés d'écart ou de Pearson, l'interprétation du graphique est la même. Lorsque le modèle utilise la fonction de liaison logit, la loi de distribution des valeurs résiduelles de la somme des carrés d'écart est plus proche de la loi de distribution des valeurs résiduelles issues d'un modèle de régression sur les moindres carrés. Plus le nombre d'essais pour chaque combinaison de paramètres de prévision augmente, plus les valeurs résiduelles de la somme des carrés d'écart et de Pearson deviennent similaires.
Interprétation
Créez un graphique des valeurs résiduelles pour déterminer si votre modèle est adapté et si les hypothèses de régression sont satisfaites. L'examen des valeurs résiduelles peut fournir des informations utiles sur l'ajustement du modèle aux données. De manière générale, les valeurs résiduelles doivent être distribuées de manière aléatoire sans aucun schéma clair ni aucune valeur aberrante. Si Minitab détermine que vos données comprennent des observations aberrantes, il les indique dans les résultats, dans le tableau Ajustements et diagnostics pour les observations aberrantes. Pour plus d'informations sur les valeurs aberrantes, reportez-vous à la rubrique Observations aberrantes.
Val. résid. norm
La valeur résiduelle normalisée est égale à la valeur résiduelle (ei) divisée par une estimation de son écart type.
Interprétation
Utilisez les valeurs résiduelles normalisées pour détecter les valeurs aberrantes. Les valeurs résiduelles normalisées supérieures à 2 et inférieures à −2 sont généralement considérées comme élevées. Le tableau Ajustements et diagnostics pour les observations aberrantes signale ces observations avec un "R". Lorsqu'une analyse indique qu'il existe de nombreuses observations aberrantes, le modèle révèle généralement des inadéquations de l'ajustement significatives. En d'autres termes, le modèle ne décrit pas de façon adéquate la relation entre les facteurs et la variable de réponse. Pour plus d'informations, reportez-vous à la rubrique Observations aberrantes.
Les valeurs résiduelles normalisées sont utiles, car les valeurs résiduelles brutes ne permettent pas toujours de détecter les valeurs aberrantes. La variance de chaque valeur résiduelle brute peut être différente en fonction des valeurs X qui lui sont associées. Il est donc difficile d'évaluer les tailles des valeurs résiduelles brutes. La normalisation des valeurs résiduelles résout ce problème en transformant les différentes variances selon une échelle commune.
Que vous utilisiez les valeurs résiduelles de la somme des carrés d'écart ou de Pearson, l'interprétation du graphique est la même. Lorsque le modèle utilise la fonction de liaison logit, la loi de distribution des valeurs résiduelles de la somme des carrés d'écart est plus proche de la loi de distribution des valeurs résiduelles issues d'un modèle de régression sur les moindres carrés. Plus le nombre d'essais pour chaque combinaison de paramètres de prévision augmente, plus les valeurs résiduelles de la somme des carrés d'écart et de Pearson deviennent similaires.
Valeurs résiduelles supprimées
Le calcul de chaque valeur résiduelle studentisée supprimée revient à supprimer systématiquement chaque observation de l'ensemble de données, à estimer l'équation de régression et à évaluer la capacité du modèle à prévoir l'observation supprimée. Chaque valeur résiduelle supprimée studentisée est également normalisée en divisant la valeur résiduelle supprimée d'une observation par une estimation de son écart type. L'omission de l'observation permet de déterminer le comportement du modèle sans elle. Si une observation possède une valeur résiduelle supprimée studentisée élevée (si sa valeur absolue est supérieure à 2), il peut s'agir d'une valeur aberrante dans les données.
Interprétation
Utilisez les valeurs résiduelles supprimées studentisées pour détecter des valeurs aberrantes. Chaque observation est omise pour déterminer la capacité du modèle à prévoir la réponse lorsqu'elle n'est pas incluse dans le processus d'ajustement du modèle. Les valeurs résiduelles supprimées studentisées supérieures à 2 ou inférieures à −2 sont généralement considérées comme élevées. Les observations signalées par Minitab suivent mal l'équation de régression proposée. Toutefois, il est normal d'obtenir quelques observations aberrantes. Par exemple, en vous fondant sur les critères de valeurs résiduelles élevées, vous pouvez vous attendre à ce qu'environ 5 % de vos observations soient signalées pour leur valeur résiduelle importante. Si l'analyse révèle de nombreuses observations aberrantes, le modèle ne décrit peut-être pas de façon adéquate la relation entre les prédicteurs et la variable de réponse. Pour plus d'informations, reportez-vous à la rubrique Observations aberrantes.
Les valeurs résiduelles supprimées et normalisées peuvent être plus utiles que les valeurs résiduelles brutes pour détecter les valeurs aberrantes. Elles corrigent les éventuelles différences de variance des valeurs résiduelles brutes dues à des valeurs de prédicteurs ou facteurs différentes.
Hi (effet de levier)
La valeur Hi, aussi appelée effet de levier, mesure la distance entre la valeur de x d'une observation et la moyenne des valeurs de x de toutes les observations d'un ensemble de données.
Interprétation
Les valeurs Hi sont comprises entre 0 et 1. Dans le tableau Ajustements et diagnostics pour les observations aberrantes, Minitab affecte un X aux observations qui présentent soit un effet de levier supérieur à 3p/n soit la valeur 0,99, en considérant en priorité la plus petite de ces valeurs. Dans la valeur 3p/n, p représente le nombre de coefficients du modèle et n le nombre d'observations. Les observations que Minitab signale par un "X" peuvent être influentes.
Les observations influentes ont un effet disproportionné sur le modèle et peuvent générer des résultats trompeurs. Par exemple, un coefficient pourra être statistiquement significatif ou non selon qu'un point influent est inclus ou exclus. Les observations influentes peuvent être des points à effet de levier et/ou des valeurs aberrantes.
En cas d'observation influente, déterminez si elle est due à une erreur d'entrée de données ou de mesure. Si l'observation n'est due ni à une erreur d'entrée de données, ni à une erreur de mesure, déterminez dans quelle mesure l'observation est influente. Tout d'abord, ajustez le modèle avec et sans observation. Ensuite, comparez les coefficients, les valeurs de p, le R2, et d'autres informations relatives au modèle. Si le modèle change de manière significative lorsque vous supprimez l'observation influente, examinez le modèle plus en détail pour déterminer si vous avez spécifié le modèle de façon incorrecte. Vous pouvez être amené à rassembler davantage de données pour résoudre le problème.
Distance de Cook (D)
La distance de Cook (D) mesure l'effet qu'a une observation sur un ensemble de coefficients dans un modèle linéaire. La distance de Cook prend en compte la valeur à effet de levier et la valeur résiduelle normalisée de chaque observation afin de déterminer l'effet de l'observation.
Interprétation
Les observations dont la valeur D est élevée peuvent être considérées comme influentes. L'un des critères couramment utilisés pour déterminer si une valeur D est élevée est qu'elle soit supérieure à la médiane de la loi F : F(0,5, p, n-p), où p représente le nombre de termes du modèle (constante comprise) et n le nombre d'observations. Une autre façon d'examiner les valeurs D consiste à les comparer à l'aide d'un graphique, tel qu'un diagramme des valeurs individuelles. Les observations possédant des valeurs D supérieures à la moyenne peuvent être influentes.
Les observations influentes ont un effet disproportionné sur le modèle et peuvent générer des résultats trompeurs. Par exemple, un coefficient pourra être statistiquement significatif ou non selon qu'un point influent est inclus ou exclus. Les observations influentes peuvent être des points à effet de levier et/ou des valeurs aberrantes.
En cas d'observation influente, déterminez si elle est due à une erreur d'entrée de données ou de mesure. Si l'observation n'est due ni à une erreur d'entrée de données, ni à une erreur de mesure, déterminez dans quelle mesure l'observation est influente. Tout d'abord, ajustez le modèle avec et sans observation. Ensuite, comparez les coefficients, les valeurs de p, le R2, et d'autres informations relatives au modèle. Si le modèle change de manière significative lorsque vous supprimez l'observation influente, examinez le modèle plus en détail pour déterminer si vous avez spécifié le modèle de façon incorrecte. Vous pouvez être amené à rassembler davantage de données pour résoudre le problème.
DFITS
La valeur DFITS mesure l'effet de chaque observation sur les valeurs ajustées dans un modèle linéaire. La valeur DFITS exprime approximativement le changement, en nombre d'écarts types, de la valeur ajustée lorsque chaque observation est supprimée de l'ensemble de données et que le modèle est réajusté.
Interprétation
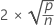
| Terme | Description |
|---|---|
| p | nombre de termes dans le modèle |
| n | nombre d'observations |
En cas d'observation influente, déterminez si elle est due à une erreur d'entrée de données ou de mesure. Si l'observation n'est due ni à une erreur d'entrée de données, ni à une erreur de mesure, déterminez dans quelle mesure l'observation est influente. Tout d'abord, ajustez le modèle avec et sans observation. Ensuite, comparez les coefficients, les valeurs de p, le R2, et d'autres informations relatives au modèle. Si le modèle change de manière significative lorsque vous supprimez l'observation influente, examinez le modèle plus en détail pour déterminer si vous avez spécifié le modèle de façon incorrecte. Vous pouvez être amené à rassembler davantage de données pour résoudre le problème.
